Generous Kefa — Adiv2
(Authors: Mediocrity, totsamyzed)
Consider each balloon color separately. For some color c, we can only assign all balloons of this color to Kefa's friends if c ≤ k. Because otherwise, by pigeonhole principle, at least one of the friends will end up with at least two balloons of the same color.
This leads us to a fairly simple solution: calculate number of occurrences for each color, like, cntc.
Then just check that cntc ≤ k for each possible c.
Complexity: O(N + K)
Godsend — Bdiv2
(Author: Mediocrity)
First player wins if there is at least one odd number in the array. Let's prove this.
Let's denote total count of odd numbers at T.
There are two cases to consider:
1) T is odd. First player takes whole array and wins.
2) T is even. Suppose that position of the rightmost odd number is pos. Then the strategy for the first player is as follows: in his first move, pick subarray [1;pos - 1]. The remaining suffix of the array will have exactly one odd number that second player won't be able to include in his subarray. So, regardless of his move, first player will take the remaining numbers and win.
Complexity: O(N)
Leha and function — Adiv1
(Author: Mediocrity)
First of all, let's understand what is the value of F(N, K).
For any subset of size K, say, a1, a2...aK, we can represent it as a sequence of numbers d1, d2...dK + 1, so that d1 = a1, d1 + d2 = a2, ..., 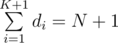 .
.
We're interested in E[d1], expected value of d1. Knowing some basic facts about expected values, we can derive the following:
E[d1 + ... + dK + 1] = N + 1
E[d1] + ... + E[dK + 1] = (K + 1)·E[d1]
And we immediately get that 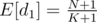 .
.
We could also get the formula by using the Hockey Stick Identity, as Benq stated in his comment.
Now, according to rearrangement inequality, 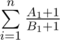 is maximized when A is increasing and B is decreasing.
is maximized when A is increasing and B is decreasing.
Complexity: O(NlogN)
Leha and another game about graph — Bdiv1
(Authors: 244mhq, totsamyzed)
Model solution uses the fact that the graph is connected.
We'll prove that "good" subset exists iff - 1 values among di can be changed to 0 / 1 so that 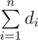 is even. If the sum can only be odd, there is no solution obviously (every single valid graph has even sum of degrees). Now we'll show how to build the answer for any case with even sum.
is even. If the sum can only be odd, there is no solution obviously (every single valid graph has even sum of degrees). Now we'll show how to build the answer for any case with even sum.
First of all, change all - 1 values so that the sum becomes even.
Then let's find any spanning tree and denote any vertex as the root. The problem is actually much easier now.
Let's process vertices one by one, by depth: from leaves to root. Let's denote current vertex as cur.
There are two cases:
1) dcur = 0
In this case we ignore the edge from cur to parentcur and forget about cur. Sum remains even.
2) dcur = 1
In this case we add the edge from cur to parentcur to the answer, change dparentcur to the opposite value and forget about cur. As you can see, sum changed its parity when we changed dparentcur, but then it changed back when we discarded cur. So, again, sum remains even.
Using this simple manipulations we come up with final answer.
Complexity: O(N + M)
On the bench — Cdiv1
(Authors: Mediocrity, totsamyzed)
Let's divide all numbers into groups. Scan all numbers from left to right. Suppose that current position is i. If groupi is not calculated yet, i forms a new group. Assign unique number to groupi. Then for all j such that j > i and a[j]·a[i] is a perfect square, make groupj equal to groupi. Now we can use dynamic programming to calculate the answer.
F(i, j) will denote the number of ways to place first i groups having j "bad" pairs of neighbors.
Suppose we want to make a transition from F(i, j). Let's denote size of group i as size, and total count of numbers placed before as total.
We will iterate S from 1 to min(size, total + 1) and D from 0 to min(j, S).
S is the number of subsegments we will break the next group in, and D is the number of currently existing "bad" pairs we will eliminate.
This transition will add T to F(i + 1, j - D + size - S) (D "pairs" eliminated, size - S new pairs appeared after placing new group).
T is the number of ways to place the new group according to S and D values.
Actually it's 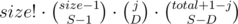 . Why? Because there are
. Why? Because there are 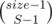 ways to break group of size size into S subsegments.
ways to break group of size size into S subsegments.
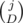 ways to select those D "bad" pairs out of existing j we will eliminate.
ways to select those D "bad" pairs out of existing j we will eliminate.
And 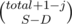 ways to choose placements for S - D subsegment (other D are breaking some pairs so their positions are predefined).
ways to choose placements for S - D subsegment (other D are breaking some pairs so their positions are predefined).
After all calculations, the answer is F(g, 0), where g is the total number of groups.
Complexity: O(N^3)
Destiny — Ddiv1
(Authors: Mediocrity, totsamyzed)
We will use classical divide and conquer approach to answer each query.
Suppose current query is at subsegment [L;R]. Divide the original array into two parts: [1;mid] and [mid + 1;N], where 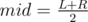 . If our whole query belongs to the first or the second part only, discard the other part and repeat the process of division. Otherwise, L ≤ mid ≤ R. We claim that if we form a set of K most frequent values on [L;mid] and K most frequent values on [mid + 1;R], one of the values from this set will be the answer, or there is no suitable value.
. If our whole query belongs to the first or the second part only, discard the other part and repeat the process of division. Otherwise, L ≤ mid ≤ R. We claim that if we form a set of K most frequent values on [L;mid] and K most frequent values on [mid + 1;R], one of the values from this set will be the answer, or there is no suitable value.
K most frequent values thing can be precalculated. Run recursive function build(node, L, R). First, like in a segment tree, we'll run this function from left and right son of node.
Then we need K most frequent values to be precalculated for all subsegments [L1;R1], such that L ≤ L1 ≤ R1 ≤ R and at least one of L1 and R1 is equal to 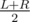 .
.
We will consider segments such that their left border is mid in the following order: [mid;mid], [mid;mid + 1], ...[mid;R]. If we already have K most frequent values and their counts for [mid, i], it's rather easy to calculate them for [mid, i + 1]. We update the count of ai + 1 and see if anything should be updated for the new list of most frequent values.
Exactly the same process happens to the left side of mid: we are working with the subsegments in order [mid;mid], [mid - 1;mid], ..., [L;mid].
Now, having all this data precalculated, we can easily run divide and conquer and get the candidates for being the solution at any [L;R] segment. Checking a candidate is not a problem as well: we can save all occurrences in the array for each number and then, using binary search, easily answer the following questions: "How many times x appears from L to R?".
Complexity: O(KNlogN)
In a trap — Ediv1
(Author: Mediocrity)
The path from u to v can be divided into blocks of 256 nodes and (possibly) a single block with less than 256 nodes. We can consider this last block separately, by iterating all of its nodes.
Now we need to deal with the blocks with length exactly 256. They are determined by two numbers: x — last node in the block, and d — 8 highest bits. We can precalculate this values and then use them to answer the queries.
Let's now talk about precalculating answer(x, d). Let's fix x and 255 nodes after x. It's easy to notice that lowest 8 bits will always be as following: 0, 1, ..., 255. We can xor this values: 0 with ax, 1 with anextx and so on, and store the results in a trie. Now we can iterate all possible values of d (from 0 to 255) and the only thing left is to find a number stored in a trie, say q, such that q xor 255·d is maximized.
Complexity: O(NsqrtNlogN)










Why a lot of likes for word "test".
Because russian version is not available. Switch the english one.
Can someone reword div1C/div2E ? What's the basic idea?
Through observation, we noticed that if a * b is a perfect square, b * c is a perfect square, the a * c is a perfect square too.So we can get T groups, and the problem changed to Source
Solution from the site
First we group all the distinct values in the array. Then we can solve the problem using dynamic programming:
Let dp[i][j] = the number of distinct arrays that can be obtained using the elements of the first i groups such that there are exactly j pairs of consecutive positions having the same value. The answer can be found in dp[distinctValues][0].
Now let's say the sum of frequences of the first i values is X. This means the arrrays we can build using the elements from these i groups have size X, so we can insert the elments of group i + 1 in X + 1 gaps: before the first element, after the last, and between any two consecutive. We can fix the number k of gaps where we want to insert at least one element from group i + 1, but we also need to fix the number l of these k gaps which will be between elements that previously had the same value. State dp[i][j] will update the state dp[i + 1][j — l + frequence[i + 1] — k].
The number of ways of choosing k gaps such that exactly l are between consecutive elements having the same value can be computed easily using combination formulas. We are left with finding out the number of ways of inserting frequence[i + 1] elements in k gaps. This is also a classical problem with a simple answer: Comb(frequence[i + 1] — 1, k — 1).
For those who are having some difficulty understanding the above analysis of Div-1 C, there is a very similar problem on Codechef which has a very nice detailed editorial with explanation of the time complexity. :)
https://csacademy.com/contest/archive/task/distinct_neighbours/solution/
And also on CSA :)
In problem Destiny — Ddiv1. I don't understand this editorial : What is K most frequent values ?
If anyone understand this editorial, please explain for me ! Thank you !
I also don't get it, but maybe it's using following neat algorithm to find majority elements.
Problem: from a sequence of N elements find one that appears more than N/2 times.
Solution: Repeat following: "Find two distinct elements and erase them.". If there is something left in the end, it will be all the same number and it's the only possible candidate for a solution.
Now we can generalize:
Problem: from a sequence of N elements find one that appears more than N/K times.
Solution: Repeat following: "Find K distinct elements and erase them.". If there is something left in the end, it will be at most K-1 different numbers and they are only possible candidates for a solution.
To use it in problem D we can apply the algoritm to interval [l, r] and obtain K-1 candidates for which we count number of appearances and obtain the answer.
Applying the algorithm to an interval can be done using segment tree.
Why we should Find K distinct elements and erase them. I don't understand. Can you explain again for me ?
Let's talk about K=2. If we repeat deleting two distinct numbers from the sequence, in the end, we'll have at most one distinct number.
Now, imagine that in the original sequence there is a number that appears more than N/2 times. It's impossible that all its appearances will be killed by the algorithm.
Why? Because every time we want to erase one of its appearances we also have to erase one other number. And we won't be able to do it because this number appears more times than all others combined. Thus, it will be the number that's only left at the end of the algorithm.
This doesn't mean that generally number that's left in the and appears more than N/2 times, but only that if there is such a number it will be left at the end of the algorithm.
Generalizing to K>2 shouldn't be hard once you get K=2.
There is another solution to problem D, with the same complexity (O(KNlogN)), using a wavelet tree (http://codeforces.com/blog/entry/52854). Build the wavelet tree for the input array. Queries are then handled similarly to "count the number of occurrences of x in [L,R]" queries, but instead of picking a branch depending on a number x, we explore both branches, but cut branches with less than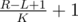 elements. At each level of the tree, at most K branches will remain, so a query is handled in time O(KlogN).
elements. At each level of the tree, at most K branches will remain, so a query is handled in time O(KlogN).
My code : 29654756. I only had to write the solve and main functions, and the solve function was obtained from cnt.
Can Div1 D be solved with Mo's algo somehow without TLE?
Yes you can use Mo to get the number of each number on each query segment and then you should use nondeterministic algorithm using rand around 80 times to draw a random id on query segment (l,r) and check whether number[id] pass the condition. The chance to win is around 99%
how did you get these numbers 80 and 99?
My logic was more like, use Mo separately for each k. but that will probably TLE
((1 — (4/5)^80) ^ 300000) * 100% = 99%
Neat! :D
I dont understand where the 4/5 comes from . Also i have implemented the idea but it dont pass test case 4. Could you check it plase? https://codeforces.com/contest/840/submission/76260302
@Akinorew I tried to implement the method as you suggested.
But I am still getting TLE on TC 5
https://codeforces.com/contest/840/submission/76963710
You can't use a map , use an array so transitions are O(1). Your algorithm is O( (n+q)sqrt(n)logn)
Thanks vextroyer i used array instead map but still got a WA in TC 20, there seems to be a logical mistake in my approach I guess. https://codeforces.com/contest/840/submission/77003213
It has nothing to do with logic but rather the implementation of the
rand()function in C++. As this article (https://codeforces.com/blog/entry/61587) explains, therand()function only gives values <RAND_MAX= 32767. TC 20 triggers this flaw. Luckily the post also provides a solution ;)I think i got the point of 4/5. Suppose if k = 5 and (r-l+1) = 100 then for a number must have frequency 21 as 100/5 = 20. So almost 4/5 probability of not getting that number on random pickup. So if we pickup random number multiple times the probability will increase as (4/5) * (4/5) * (4/5) * ... . So if we pick up random numbers 70 or 80 times the probability of getting the expected will be 99%.
You don't need a randomized algorithm for Mo's, although it is very neat.
Still waiting for Div1 E.
Since the editorial for Div-1 E is not yet available, I decided to explain my solution to it on the basis of this comment.
Each mask can consist of atmost 16 bits. We deal with both halves separately. For a given query (u, v), we process the path in blocks of 256. For any vertex on the path from u to v (let it be a), the distance from v will be of the form 256*A+B, where A>=0 and 0<=B<256. If we process the path in blocks of 256, the "A" values for all vertices in the block will be same.
Note that 256*200 > 50000, so there will be atmost 200 blocks. We precompute for each vertex, considering it as the lowest vertex of the block, for all i such that 0<=i<=200, what the max XOR we can get using the most significant 8 bits. If you see my code,
best_most_significant_eight[v][i] denotes the max xor we can get considering only the most significant 8 bits in the block of size <= 256, with the lowest vertex being v and i is the "A" value of the vertices in this block. eg. For a node at distance 257 (256*1+1) from node v, the "A" value is 1.
Now, we need to handle the lowest 8 bits. For any block, we should consider the lowest 8 bits of only those nodes whose highest 8 bits give us the max xor obtained previously. This we can do using precomputation too. Again, with reference to my code, best_lower_significant_eight[v][i] denotes the max xor we can get using lower 8 bits (i.e. using the "B" value) for the block with lowest vertex v and the highest 8 bits are i.
We can calculate best_lower_significant_eight[][] by just iterating over the immediate 256 ancestors of every vertex.
We can calculate best_most_significant_eight[][] by inserting all the values of the immediate 256 ancestors in the trie and then querying for the max XOR, for all i from 0 to 200.
Now all that remains is to handle the vertices in the topmost (maybe incomplete) block while solving a query. In that case, since there are atmost 256 vertices to check, we can just run through them all and update our answer.
You can see my code for this implementation. Time complexity is roughly O(N*256 + Q*256).
Can someone please explain Leha and function — Adiv1 ?
One important step is to prove F(N,K) = (N+1) / (K+1).
For any subset of size K, we sort them as a_1, a_2, ..., a_K with a_1 < a_2 < ... < a_K. Here we construct another sequence which is d_i, d_1 = a_1, d_2 = a_2 — a_1, ..., d_K = a_K — a_{K-1}. Note the sequence {d_i} and sequence {a_i} are bijection.
We add another d_{K+1} = N + 1 — a_K. Note d_i are identically distributed, which means if we switch any two of d_j, d_k and keep other d unchanged, the correspoding {a_i} is still valid (Only the value of a_j changed).
So E(d_1) = E(d_2) = ... = E(d_{K+1}).
Also, we have E(d_1 + d_2 + ... d_{K+1}) = N+1. So E(d_1) = (N+1) / (K+1).
Since a_1 is the smallest of a_i, due to definition, we have F(N,K) = E(a_1) = E(d_1) = (N + 1)/(K + 1).
What left is just to Google "rearrangement inequality".
I would have expected that we need to calc F(N,K) somehow and use these values. It seems that this is not necessary. Why?
Hi! Can anyone please explain this sample test case from Div2D.
Input:
Output:
0 output means that there are no edges in the good subset and the original graph already satisfies all the mentioned conditions( for every vertex i, di = - 1 or it's degree modulo 2 is equal to di. ).
In this graph:
Moreover, if I remove 5th edge(2 4) then all conditions are satisfied but that would be a Wrong Answer.
Can anyone point me in the right direction? I am unable to understand this question.
Thanks :)
As you said 0 means there are NO EDGES in the good subset. There are only the vertices, i. e. every node's degree is 0, which satisfies the conditions.
Can anyone please explain Div2-D/Div1-B ? I didn't understand the solution given in the editorial.
Can someone please explain how to solve div 2 C or div 1 A.
You can see my comment above to sushant_. :)
Hello,
The statement in the editorial Adiv1 "as Benq stated in his comment",
so where can I find Benq's comment?
Thanks in advance.
See here.
Thanks!
can someone please help me understand div1 A . i learnt what is meant by expected values but i am unable to understand the proof given in the editorial . Please help
Hello! I don't know if you are still interested in this problem, but I'd like to share my thought with you. As you can see in the tutorial, any element $$$a_i$$$ in the set with size of $$$k$$$, can be represented by an array $$$d$$$, where $$$\sum\limits_{j=1}^{i}d_i=a_i$$$. And let's denote $$$\sum\limits_{i=1}^{k+1}d_i = N + 1$$$. Obviously, $$$d_i$$$ is identically distributed, which means $$$E(d_1) = E(d_2)=....=E(d_{k+1})$$$. Because of the linearity of expectation, $$$N+1=E(\sum\limits_{i=1}^{k+1} d_i)=\sum\limits_{i=1}^{k+1}E(d_i)$$$,and it's equal to $$$(k+1)E(d_1)$$$. So $$$E(d_1)=\dfrac{N+1}{K+1}$$$. Feel free to ask me if you still have any question!
Why are $$$ d_i $$$ identically distributed?
Because all $$$d_i$$$ have the same possiblity to be $$$1,2,....,N-1$$$.They are symmetric and equivalent.
Do you have a rigorous proof? Seems kinda handwavish to me.
Hmm... I think it's rigorous enough. Is there anything not clear enough?
Well, on 70th edit i think i got kinda close to the rigorous proof.
Let's compute possible values for $$$ d_s, 1 \leq s \leq k $$$. You must have $$$ \sum_s d_s = N + 1 $$$ and you already used up $$$ s - 1 $$$ of them, which implies that you only have $$$ N + 1 - (s-1) = N - s + 2 $$$ left. $$$ d_r, s < r \leq k + 1 $$$ must be positive too. Let's suppose they are all $$$ 1 $$$ to maximize $$$ d_s $$$. There are $$$ k + 1 - s $$$ of them, so that gives you a maximum of $$$ N-s+2 - k - 1 + s = N-k+1 $$$ for $$$ d_s $$$. Note that it does not depend on $$$ s $$$, so at least possible range is the same for all of them.
I still don't get why expectations are the same though.
The upper bound of $$$d_i$$$ is $$$N+1-K$$$.It's not that important...... Assume that you have gotten an array {$$$d_i$$$}. Then you can exchange $$$d_1$$$ and $$$d_2$$$,it will form a new {$$$d_i$$$}. So for any number $$$d_1$$$ can be,$$$d_2$$$ can also have the same possibility to be that number. Similarly, all $$$d_i$$$ have the same possibility to be a specific number. So I say it's symmetric...Then according to the definition of expectation:$$$E(x)=\sum i*P(x = i)$$$,you can know their expectations are equal.
If $$$k = 2$$$ erase two different elements until all left elements are equal and then count the number of occurrences of this element in the whole array. When $$$k \leq 5$$$ we can use similar algorithm: until there are at least $$$5$$$ different elements remove a $$$5$$$-tuple of different elements, and once there are at most $$$4$$$ different elements count for all of them number of occurrences in whole array. Now for each node of segment tree we can store any possible final state of array on this segment represented as 4 pairs (value, count). The only thing left is implementing merging results for two segments efficiently enough.
DIV 1 A can easily be done as Printing largest element of a parallel with the smallest element of b then the 2nd largest element parallel with the 2nd minimum of b and so on.. 83756733
yes. this is the solution. but coming up with this and proving why it works is tough part xP
Not so Tough though :3
Can problem Div1 D (Destiny) solved using a persistent segment tree ? I tried but I'm getting WA on test 6 which makes me think the logic is wrong? I'm not sure if it's just a bug somewhere. https://codeforces.com/contest/840/submission/115038909
Sorry for the necropost!