There are at most 300 students, and thus we can directly simulate the whole process, i.e., what happens in each minute. The simulation terminates when no students are left.
The implementation is straightforward. We can enumerate each letter, and only those that appear exactly once in the corresponding row and column should be output.
An interesting problem.
Suppose that Δ x elements are taken away. To guarantee that the n - 1 sums keep the same, the changing quantity for each element must be - Δ x, Δ x, - Δ x, Δ x, .... Therefore, if n is an even number, it is impossible to take away any elements, since the total sum can not be changed. For an odd number n, it can be seen that to take away Δ x elements, we have to carry out 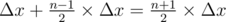 moves. For each minute, at most m moves can be conducted, and thus
moves. For each minute, at most m moves can be conducted, and thus 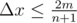 . Given k minutes, we can carry out at most
. Given k minutes, we can carry out at most 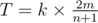 moves. However, the value m = min(a[1], a[3], ...a[2n + 1]) has provided an upper bound (the index starts from 1), and thus the answer should be min(T, m).
moves. However, the value m = min(a[1], a[3], ...a[2n + 1]) has provided an upper bound (the index starts from 1), and thus the answer should be min(T, m).
The description is long but it turns out to be a traversal on a q-ary tree, which can be solved by using DFS. One important trick is to store the results that have been obtained at each node to avoid TLE.
The trick is how to find out the next position with constant complexity so that the total complexity is (n × m × n × m). For each position with an arrow, we assign four links to denote the nearest four positions with arrows that it can reach, in left, right, up and down directions, respectively. This process can be completed with complexity O(n × m), by using the prefix and suffix idea.
When we move from the current position to the next one, we should update the links assigned to the four nearest arrows as well, since after moving, the current arrow will disappear. Suppose that the current position is P, and its four links are P[L], P[R], P[U], P[D], denoting that the nearest left, right, up and down arrows. When P disappears, the nearest right arrow of P[L] should be P[R], and the nearest left arrow of P[R] is P[L], and the nearest upside arrow of P[D] is P[U], and the nearest downside arrow of P[U] is P[D].
After the above updating, we can always find out the next arrow with constant complexity. Remember to restore the initial links after every time we complete DFS.









