Hello everyone!
Over last few years number of standard algorithms and structures (dfs, FFT, segment tree, suffix automaton, ... Gomory-Hu tree) didn't change much, at least in my perception. Most of fresh tasks require pure creativity (tasks on atcoder.jp being most prominent example) or unusual combination of well-known blocks. Some tasks are even pure combinatorics math problems (I'm a big fan of these).
But I think there still are room to bring some new "primitive" structures. Let's form a list of interesting stuff that are unpopular or unknown!
My first thoughts are palindromic tree and multipoint evaluation (computes values of polynomial of degree n in n points in 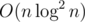 time).
time).











DP optimization used in IOI 2016 Aliens
Btw does the multipoint evaluation you mentioned work for any commutative ring , or does it only work for certain special rings?
No, you need FFT for the multipoint evaluation.
Maybe Wavelet (tree|matrix|array)? I haven't heard about them until recent time.
The impressive algorithm in recent years for me is solving linear recursion.
I was very surprised when first saw this problem in 2014 in Petrozavodsk.
Now (after all this years...) I think the best explanation of this trick is using generating functions. In a nutshell, you need to calculate first n coefficients of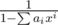 , which can be done in
, which can be done in  using FFT.
using FFT.
Also, continuing this line, one can calculate first n coefficients of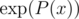 , P(x)a,
, P(x)a, 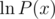 in
in  using Newton's method.
using Newton's method.
I think the simplest explanation is calculating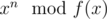 , where f(x) = xk - a1xk - 1 - ... - ak is the characteristic polynomial. You just say that xn = a1xn - 1 + ... + akxn - k and repeat it until only powers less than k remain. It is literally the same as calculating an in the naive way. It also works for big values of n with binary exponentiation in
, where f(x) = xk - a1xk - 1 - ... - ak is the characteristic polynomial. You just say that xn = a1xn - 1 + ... + akxn - k and repeat it until only powers less than k remain. It is literally the same as calculating an in the naive way. It also works for big values of n with binary exponentiation in 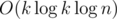 .
.
I also was surprised when I heard of it on algebra lesson in the first year in university. Kind of sad that every schoolkid knows how to solve this problem with matrix multiplication but so few people know about this trick.
How do you use newton's method to find first n coefficients of P(x)a, and others?
I find P(x)a case particularly surprising because if there exists such an algorithm, then you can find ab without a factor of .
.
This is what I saw on some chinese paper.
Calculating the reciprocal of a polynomial is quite well-known. See for example here.
To calculate ln(A(x)), let B(x) = ln(A(x)). Then by Chain Rule,
We can find A'(x) in O(n) time and in
in  time. Multiplying these polynomials take another
time. Multiplying these polynomials take another  time. Finally, integrate the result in O(n) time.
time. Finally, integrate the result in O(n) time.
Calculating exp(A(x)) is more involved. Let f(x) = eA(x), and let g be a function such that g(f(x)) = 0 = ln(f(x)) - A(x).
Firstly, we can compute the constant term of f(x) by using the Maclaurin series. Suppose we know the first n terms of f(x), call it f0(x), thus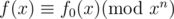 .
.
By Taylor's expansion,
Here g(2) denotes the second differential of g.
Thus,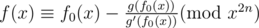 ,
,
Substituting g(f0(x)) = ln(f0(x)) - A(x), we get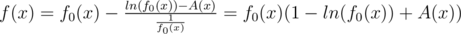 .
.
Thus, it is sufficient to compute the last term to get the first 2n terms of f. Similar to finding the inverse, we can prove that this works in time.
time.
Now, to calculate P(x)a, then just calculate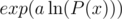 . Complexity is still
. Complexity is still  .
.
But how to calculate the 0th term in exponent? It seems to be impossible if polynomials 0th term isn't zero. Also to integrate the result in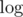 you have to know 0th term.
you have to know 0th term.
Btw, the rule you mentioned is exactly Newton's method and it can be used to calculate terms of any proper function.
You're right. I forgot to mention that in calculating log we assume the constant term is 1 and for exp we assume the constant term is 0.
Thus, before calculating P(x)a we need to convert P(x) to a polynomial with constant term 1. Let cxd be the smallest nonzero term in the polynomial. Then,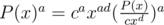 and we can calculate
and we can calculate 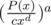 using the method above because the constant term is 1.
using the method above because the constant term is 1.
Things came up after WF 2014 (the end of my career):
Two most commonly used technique on ProjectEuler: (a) Berlekamp–Massey algorithm (b) O(n2 / 3) or O(n3 / 4) sieve-like algorithm (I don't know what it should be called exactly)
Novel use of segment tree (It is called "SGT Beats" in China). [Add some description]
Tutte Matrix.
to be continued.
Can you post a description/link for the second technique?
Please continue :)
please continue
Add the description please
LiChao tree for convex hull trick
Ji Driver segment tree
There are so much cool named tricks in China, why are they so unknown outside China?
Could you give a slight overview of this segment tree ?
There are many mathematical things that uses in competitive programming, but I've never used differential or integral in competitive programming problems.
Sometimes derivatives are used to find optimum values of functions. (see this for example)
It does happen, see ACM ICPC Finals 2012 problem B for example.
Polynomial interpolation always seems like magic to me. Some of my favourite problems that can be solved with it are this and this.
Also task Infinity Binary Embedding of yours is a good example (can be found here).
Yes, I'm very proud of this task. =) It doesn't exactly involve interpolation from values though.
Some open problems regarding "aliens trick" :
For so-called "jiry_2 SGT", it's conceptually simple. Considering "sum of distinct numbers in each nodes" as the potential function, the 2nd minimum/maximum is to ensure you reduce the potential for each "extra" SGT recursion you make.
IMO "aliens trick" is Lagrange multiplier. For the APIO task you posted, add to the objective function and try to minimize using optimization tool.
to the objective function and try to minimize using optimization tool.
Seems like my english was awful :/ I was wondering how to print the optimal splitting sequence, not only the answer
It is really amazing for me to hear so many extremely advanced techniques...
Perhaps this is a little away from the topic, but I was always wondering how the first person came up with such ingenious techniques. Some of them might just be advanced or improved versions of relatively mature techniques, but the other ones seem considerably original and creative. What is the inspiration behind these techniques? Is it like science that people make improvement based on the previous results?
How about Dominator Tree in directed cyclic graph?
Isn't that older than me?
Maybe it is old for a half-step to legendary like you but for a blue one like me... (I just know about the "name" in Barcelona Bootcamp a while ago :v)
And I think you look older than it :p
But the age of an algorithm is not measured based on when you or me learnt it but based on when it was published/introduced. And Tarjan's paper on fast algorithm for dominator tree was published in 1979 :)
Okay Okay. You are younger than the that old algorithm. :))
I have a question to ask. From your comment, I guess that you, bloody red coders, seem to learn algorithms from original papers and do your own implementation rather than finding a tutorial on some community. Is it true?
(Since I want to know if my current way of learning is wrong: find tutorials and search for nice codes from high rated coders to read)