Hallo everyone,
Do you know any simple formulas that are often unknown to many? For me, some can be mentioned are
Graph: Euler characteristic, Handshaking theorem, Caley Formula, Kirchhoff's theorem, Kőnig's theorem
Polygon: 2-Ear Theorem, incenter formula of a triangle, pick theorem, Shoelace Formula
Logic: Pigeonhole
Prime: Fermat, Wilson's theorem
Number: McNugget theorem
Fibonacci: Zeckendorf's theorem
Counting: Burnside Lemma, stars and bars
Combinatorics Identity: Vandermonde's Identity, Hockey-stick identity
Math: Linearity of Expectation
Other: harmonic series sum
... And what about you? Can you share some?
Thank you.










Well I suppose if you included Pigeonhole, then Harmonic Series sum can be included too. It's just useful to know (sometimes used in problems):
a ha, that is also what I mean, in the past, I never knew why sieve ran so fast until I saw this formula
I will update in the post
Harmonic Series can be used to explain linearithmic complexity in solution for this problem:
http://codeforces.com/problemset/problem/414/B
Here is editorial: http://codeforces.com/blog/entry/11470
It's n*log(n) because you loop i from 1 up to n, and inside that loop you loop multiples of i up to n, which will run in n/1 + n/2 + ... n/n which is n*(1/1 + 1/2 + ... 1/n) = n*log(n) as Noam527 has described.
The sieve is well-known.
However, something that is not as well-known is that the sieve can be modified to be run in O(n) time.
vector <int> is_prime(LIMIT, true); is_prime[0] = is_prime[1] = false; vector <int> primes; for(int i = 2; i < LIMIT; i++) { if(is_prime[i]) primes.push_back(i); for(int j = 0; j < primes.size() && i*primes[j] < LIMIT; j++) { is_prime[i*primes[j]] = false; if(i%primes[j] == 0) break; } }This is often used in problems. In particular:
let's you create list of all numbers from with their divisors 1..N in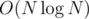 .
.
Pick's Theorem is One Such theorem. Problems are there on this topic.
that's a nice one
I will update in the list :)
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
Chicken McNugget theorem.
The motivation is in McDonald Chicken McNuggets, which come in packs of 4, 6, 9, and 20. If you wanted to troll them, you could ask for a pack of 11 (the largest amount of chicken McNuggets they can't make).
https://artofproblemsolving.com/wiki/index.php?title=Chicken_McNugget_Theorem
For two coprime positive integers m and n, that largest number that cannot be written as am + bn (cannot be made by adding up m and n) will be m*n — m — n.
Not sure why it works (could not under stand proof :P), so it would be great if some smarter folks expanded on this.
Such a formula does exist :o what a surprise?
Updated
Yes, unfortunately this only works for two variables. There is no general formula that works for 3+ variables, but there are methods to compute them in polynomial time.
As a clarification: numbers that can be made are called chicken mcnugget numbers. Numbers that cannot be made are called Frobenius numbers.
Described Here: https://en.wikipedia.org/wiki/Coin_problem
It's actually very easy to see that if you look at it as a graph problem. Remainders modulo m are vertices and there are edges from each vertex x to (x+n)%m of length 1, because this is equivalent to adding n once. Now you can see that by reaching shortest path from 0 to a vertex we get the smallest possible number of "+n" parts (crucial here is that adding m doesn't change the remainder modulo m).
You can notice that the distances are 1,2,3.. in some order and the last one is exactly m (n-1)-n
Thank you so much! I've always felt guilty about not getting this but the graphs explanation is much clearer than the maths explanation :P
I just tried to draw it out.
I am confused about this part "You can notice that the distances are 1,2,3.. in some order and the last one is exactly m (n-1)-n"
How could the distance between any two vertices in this graph be m (n-1) — n when the greatest distance possible is m-1? (there are m vertices)
I have found the Shoelace Formula to be extremely useful in some instances (esp with coordinate/geometry problems).
A nice trick for determining whether a bunch of points are collinear: if they enclose an area of 0 then they lie on a line or are the same point -- meaning the shoelace formula should give 0 as well.
:o I use it a lot but I never thought it had a name :p
Updated
Maybe Faulhaber's Formula for calculating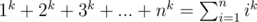 ?
?
Some Pythagorean triplet's properties?
I would not really think that it is simple :V
Interestingly, there are k3logn and k2 solutions to this problem.
nvm, fail
i = sqrt(-1)
I think that what he meant, right?
ah yes, thanks, used to j :D
True, but would you mind explaining a bit about its application in CP (some problems for example)
Since I rarely see any problems that require complex number directly.
I met a problem 102E - Вектора, whose solution was derived based on complex number. But it does not use the above equation....
Not very sure about CP, but it is neccessary for trig-bashing e.g. Bary Bash.
hahahahha
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
2 + 2 = 4 — 1 = 3 Quick Maths!
Oh it is too simple!!! but not really unknown to many
Maffs*
Man's not hot...
Could you please edit your post and make the theorems point-wise using bullets or something? Right now it looks unpleasant to read.
done
Cayley's formula is the number of spanning trees of N nodes which is equal to NN - 2
Number of spanning trees in complete bipartite graph GX, Y is : XY - 1 × YX - 1
Such that
X : is the number of nodes in the first set.
Y : is the number of nodes in the second set.
nice one :)
updated
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
I have met a problem about several days before, which used "Fermat's theorem on sums of two squares" (I am not sure of the exact name of this theorem). This theorem has a simple description but perhaps a little bit complicated proof. It states that for any prime integer p > 2, it can be written as p = a2 + b2, where both a and b are positive integers, if and only if p mod 4 = 1.
Thanks a lot for your effort. It would be really nice if you also go on adding the links for these theorems. Others might help for the links they found, by commenting.
Here are few which are used in competitive programming sometimes:
Could u give me a problem where Jensen's inequality is used... thank you.
I never used it in any informatics problem, but much in math problems. Maybe it can be used in proving correctness of solution or reducing some cases while solving problem.
I don't remember any problem, but I have seen it being used to prove quadrangle inequality in divide and conquer DP optimization.
Wow, so many, so nice :D
I have updated the blog from some of those, but... not all.
For example, I think that the Bertrand's theorem is so obvious. For Goldbach's theorem, I have never really seen a problem that can be "indirectly" solve by it (problems for it are all obviously the definition). Faulhaber's formula, I do not think it is simple in anyway. Jensen's inequality, I think is more suitable for proving rather than implementing. Am I wrong? If so, please just tell me :D
And Burnside theorem is indeed powerful. That is my motivation for writing this blog
Zeckendorf's theorem.
A problem using this theorem: http://codeforces.com/problemset/problem/126/D .
The winning strategy for fibonacci nim also uses the theorem.
That's a very nice one :o
I myself also have doubt that it is true but I never try to prove (which I cannot) or bother about it (since not many problems like that anyway). Now I know something new, thank you.
I have found the Paleka's lemma to be useful:
If and only if it contains "circumcircles" and the intersection of three lines which pass through six distinct points, it can be done using radical center.
Maybe can you tell me a bit about the problem/situation where you found it helpful? It maybe be very great but for now, I dont really get its usefulness from your discription. Thank you
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
Auto comment: topic has been updated by duckladydinh (previous revision, new revision, compare).
Ok, maybe all you pros knew it long ago, but I learned inverse mod finding of prime mod with fermat's little theorem just yesterday
Same ideas :D
The first application I could think of (myself :D) from Fermat theorem is the inverse mode for prime. No other use in programming for it until now :v
It is already included
I think you can add Catalan Numbers in Number theory/Combinatorics or Counting.
For some reason people don't usually use barycentric coordinates in problems where they can help. Let's say that a point P has masses (x, y, z) wrt triangle ABC with sides a, b, c and angles α, β, γ (side with length a has endpoints B and C, angle α is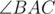 , the same naming with other sides and angles) if x + y + z ≠ 0 and (x + y + z)P = xA + yB + zC. This can help to find some points associated to a triangle:
, the same naming with other sides and angles) if x + y + z ≠ 0 and (x + y + z)P = xA + yB + zC. This can help to find some points associated to a triangle:
I use "masses" instead of "barycentric coordinates" since the sum of barycentric coordinates should equal 1. The points listed above can be found in one line if one has a written Point class with addition and multiplication by a real. Of course, sometimes (for example, for orthocenter of circumcenter) it's easier to intersect two lines, but there are problems where masses optimize time and efforts.