Modify the letters as the problem requires.
We use a[i] to denote the number of a non-negative integer i while using b[i] to denote the number of a negative integer - i (i > 0). For any positive integer i, we have min(a[i], b[i]) choice, while for i = 0, we have 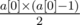 choice. Thus, the final answer should be
choice. Thus, the final answer should be 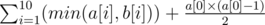 .
.
We enumerate all the feasible combination of boys and girls, and only consider those that satisfy the requirements. Then, the main issue is to calculate 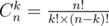 . Although n is not larger than 30, it is still difficult (or infeasible) to compute n!. Thus, we modify the formula as
. Although n is not larger than 30, it is still difficult (or infeasible) to compute n!. Thus, we modify the formula as  , which could handle all n ≤ 30.
, which could handle all n ≤ 30.
The solution is first DFS, and then BFS.
At first, we implement DFS to find the unique cycle and all the nodes on the cycle. Then, we implement BFS with all of these nodes as the starting state, and update the distance of each node. One can find plenty of materials about how to find the cycle based on DFS.
131E - Yet Another Task with Queens
There exists a solution with complexity of O(m). We first enumerate all the queens, and update three values for each row. The first value is the total number of queens in the current row; the second value is the position of the leftmost queen; the third value is the position of the rightmost queen. Then, we enumerate all the queens again. For any queen in the i-th row, if the total number of queens in this row is less than or equal to 1, then no queen could threaten it; otherwise, there will be exactly one or two queens that could threaten it, depending on whether it is the leftmost one or the rightmost one, which can be checked with complexity O(1) since we have stored the positions of the leftmost and rightmost queens.
Similarly, for each column, we update three values as well. The first value is the total number of queens in the current column; the second value is the position of the top queen; the third value is the position of the bottom queen. The following operations are almost the same as done when we deal with rows.
Finally, we deal with the diagonals of + 45 and - 45 degrees, respectively, and the answer is thus obtained.
The idea is that we use exhaustive enumeration to deal with one dimension while using “two pointers” to deal with the other dimension, which gives a solution of complexity O(n3).
We use dp[i][j] to denote the total number of stars from column 1 to column j, for the i-th row. Then, we enumerate all the feasible two boundaries of columns. For each combination, we adopt two pointers p1 and p2, both starting from 0, and move p2 downwards while letting p1 chase after p2. This behaves like a sliding window, and we modify its position and size so that it contains t stars, where t is the minimum integer that is not less than k. During this process, we update the answer.









