Hi, all!
This is not Tommyr7, but the impostor behind the round again (guess who I am? :P). The statements are written by me. Thank you, everyone, and hope you've all enjoyed the round!
Any feedback on problems and tutorials are welcome — we look forward to doing even better in the future!
Here are some of the detailed tutorials!
Tutorials
934A - Совместимая пара
Author quailty / Preparation quailty / Tutorial quailty
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll INF=(1LL<<60)-1;
ll a[55],b[55];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=1;i<=m;i++)
scanf("%lld",&b[i]);
ll res=INF;
for(int i=1;i<=n;i++)
{
ll now=-INF;
for(int j=1;j<=n;j++)if(j!=i)
for(int k=1;k<=m;k++)
now=max(now,a[j]*b[k]);
res=min(res,now);
}
printf("%lld\n",res);
return 0;
}
934B - Большая ставка
Author Tommyr7 / Preparation cyand1317 / Tutorial cyand1317
#include <bits/stdc++.h>
using namespace std;
int n,k;
int main()
{
scanf("%d",&k);
if (k>36) printf("%d\n",-1);
else
{
while (k>0)
{
if (k>=2)
{
printf("%d",8);
k-=2;
} else
{
printf("%d",9);
k-=1;
}
}
printf("\n");
}
return 0;
}
933A - Извилистые движения
Author visitWorld / Preparation visitWorld / Tutorial visitWorld
#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = (x), _ = (y); i < _; ++i)
#define down(i, x, y) for (int i = (x) - 1, _ = (y); i >= _; --i)
#define fi first
#define se second
#define mp(x, y) make_pair(x, y)
#define pb(x) push_back(x)
#define bin(x) (1 << (x))
#define SZ(x) int((x).size())
using namespace std;
typedef pair<int, int> pii;
typedef vector<int> Vi;
typedef long long ll;
template<typename T> inline bool upmax(T &x, T y) { return x < y ? (x = y, 1) : 0; }
template<typename T> inline bool upmin(T &x, T y) { return x > y ? (x = y, 1) : 0; }
const int MAX_N = 2005;
int pre[MAX_N][2], suf[MAX_N][2];
int g[MAX_N][MAX_N][2][2];
int w[MAX_N], N;
int main() {
scanf("%d", &N);
rep (i, 0, N) { scanf("%d", &w[i]); w[i]--; }
rep (i, 0, N) {
if (i) memcpy(pre[i], pre[i - 1], sizeof pre[i]);
down (j, 2, w[i]) upmax(pre[i][j], pre[i][w[i]] + 1);
}
down (i, N, 0) {
if (i < N - 1) memcpy(suf[i], suf[i + 1], sizeof suf[i]);
rep (j, 0, w[i] + 1) upmax(suf[i][j], suf[i][w[i]] + 1);
}
int ans = pre[N - 1][1];
rep (i, 0, N) {
rep (a, 0, w[i] + 1) rep (b, w[i], 2) {
g[i][i][a][b] = 1;
}
}
rep (l, 1, N) rep (i, 0, N - l) {
int j = i + l;
rep (l, 0, 2) rep (a, 0, 2 - l) {
int b = a + l;
g[i][j][a][b] = max((a < 1 ? g[i][j][a + 1][b] : 0), (b ? g[i][j][a][b - 1] : 0));
upmax(g[i][j][a][b], g[i + 1][j][a][b] + (b == w[i]));
upmax(g[i][j][a][b], g[i][j - 1][a][b] + (a == w[j]));
upmax(ans, (i ? pre[i - 1][a] : 0) + g[i][j][a][b] + (j < N - 1 ? suf[j + 1][b] : 0));
}
}
printf("%d\n", ans);
return 0;
}
933B - Генеральная уборка
Author Tommyr7 / Preparation cyand1317 / Tutorial cyand1317
#include <bits/stdc++.h>
using namespace std;
long long p;
int k;
int cnt=0;
int ans[107];
int get()
{
int x=p%k;
if (x<0) x+=k;
return x%k;
}
int main()
{
scanf("%lld%d",&p,&k);
while (p!=0)
{
++cnt;
ans[cnt]=get();
p-=get();
p/=(-k);
}
printf("%d\n",cnt);
for (int i=1;i<=cnt;i++)
printf("%d ",ans[i]);
printf("\n");
return 0;
}
933C - Цветное зрелище
Author quailty / Preparation quailty / Tutorial quailty
#include<bits/stdc++.h>
using namespace std;
typedef long double db;
const db eps=1e-12;
struct Point
{
db x,y;
Point(){}
Point(db _x,db _y):x(_x),y(_y){}
Point operator + (const Point &t)const
{
return Point(x+t.x,y+t.y);
}
Point operator - (const Point &t)const
{
return Point(x-t.x,y-t.y);
}
Point operator * (const db &t)const
{
return Point(x*t,y*t);
}
Point operator / (const db &t)const
{
return Point(x/t,y/t);
}
bool operator < (const Point &t)const
{
return fabs(x-t.x)<eps ? y<t.y : x<t.x;
}
bool operator == (const Point &t)const
{
return fabs(x-t.x)<eps && fabs(y-t.y)<eps;
}
db len()const
{
return sqrt(x*x+y*y);
}
Point rot90()const
{
return Point(-y,x);
}
};
struct Circle
{
Point o;
db r;
Circle(){}
Circle(Point _o,db _r):o(_o),r(_r){}
friend vector<Point> operator & (const Circle &c1,const Circle &c2)
{
db d=(c1.o-c2.o).len();
if(d>c1.r+c2.r+eps || d<fabs(c1.r-c2.r)-eps)
return vector<Point>();
db dt=(c1.r*c1.r-c2.r*c2.r)/d,d1=(d+dt)/2;
Point dir=(c2.o-c1.o)/d,pcrs=c1.o+dir*d1;
dt=sqrt(max(0.0L,c1.r*c1.r-d1*d1)),dir=dir.rot90();
return vector<Point>{pcrs+dir*dt,pcrs-dir*dt};
}
}p[5];
struct DSU
{
int fa[5];
void init(int n)
{
for(int i=1;i<=n;i++)
fa[i]=i;
}
int find(int x)
{
return fa[x]==x ? x : fa[x]=find(fa[x]);
}
void merge(int x,int y)
{
x=find(x),y=find(y);
if(x!=y)fa[x]=y;
}
}dsu;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
cin>>p[i].o.x>>p[i].o.y>>p[i].r;
vector<Point> all;
dsu.init(n);
int e=0;
for(int i=1;i<=n;i++)
{
vector<Point> pat;
for(int j=1;j<=n;j++)if(i!=j)
{
vector<Point> tmp=p[i]&p[j];
if(!tmp.empty())dsu.merge(i,j);
for(int k=0;k<(int)tmp.size();k++)
all.push_back(tmp[k]),pat.push_back(tmp[k]);
}
sort(pat.begin(),pat.end());
e+=unique(pat.begin(),pat.end())-pat.begin();
}
sort(all.begin(),all.end());
int v=unique(all.begin(),all.end())-all.begin(),c=0;
for(int i=1;i<=n;i++)
c+=(dsu.find(i)==i);
cout<<e-v+c+1<<endl;
return 0;
}
#include <cmath>
#include <cstdio>
#include <algorithm>
static const int MAXN = 3;
static const double EPS = 1e-9;
static int n;
static int x[MAXN], y[MAXN], r[MAXN];
// -2: internally separate
// -1: internally tangent
// 0: intersecting
// +1: externally tangent
// +2: externally separate
static int g[MAXN][MAXN];
// Number of points passed by all three circles
static int conc;
inline int rel(int a, int b)
{
int dssq = (x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]),
dfsq = (r[a] - r[b]) * (r[a] - r[b]),
smsq = (r[a] + r[b]) * (r[a] + r[b]);
if (dssq < dfsq) return -2;
else if (dssq == dfsq) return -1;
else if (dssq < smsq) return 0;
else if (dssq == smsq) return +1;
else return +2;
}
inline void get_intersections(int a, int b, double ix[2], double iy[2])
{
double angle = atan2(y[b] - y[a], x[b] - x[a]);
double ds = sqrt((x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]));
double delta = acos((ds * ds + r[a] * r[a] - r[b] * r[b]) / (2.0 * r[a] * ds));
ix[0] = x[a] + r[a] * cos(angle + delta);
iy[0] = y[a] + r[a] * sin(angle + delta);
ix[1] = x[a] + r[a] * cos(angle - delta);
iy[1] = y[a] + r[a] * sin(angle - delta);
}
inline bool on_circle(int a, double x0, double y0)
{
return fabs((x[a] - x0) * (x[a] - x0) + (y[a] - y0) * (y[a] - y0) - r[a] * r[a]) <= EPS;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d%d%d", &x[i], &y[i], &r[i]);
for (int i = 0; i < n - 1; ++i)
for (int j = i + 1; j < n; ++j)
g[i][j] = g[j][i] = rel(i, j);
conc = 0;
if (n == 3) {
for (int i = 0; i < 2; ++i) {
for (int j = i + 1; j < 3; ++j) if (g[i][j] >= -1 && g[i][j] <= +1) {
int k = 3 - i - j;
double ix[2], iy[2];
get_intersections(i, j, ix, iy);
if (on_circle(k, ix[0], iy[0])) ++conc;
if (on_circle(k, ix[1], iy[1]) && g[i][j] == 0) ++conc;
break;
}
if (conc != 0) break;
}
}
if (n == 1) {
puts("2");
} else if (n == 2) {
puts(g[0][1] == 0 ? "4" : "3");
} else if (n == 3) {
int x[3] = { g[0][1], g[0][2], g[1][2] };
std::sort(x, x + 3);
if (x[0] == -2) {
printf("%d\n", 4 + (x[1] == 0) + (x[2] == 0));
} else if (x[0] == -1) {
if (x[1] == -1) {
printf("%d\n", x[2] == -1 ? 4 : (6 - x[2]));
} else {
switch (x[1] * 10 + x[2]) {
case 00: printf("%d\n", 7 - conc); break;
case 01: puts("6"); break;
case 02: puts("5"); break;
case 11: case 12: case 22: puts("4"); break;
default: puts("> <");
}
}
} else if (x[0] >= +1) {
puts(x[0] == +1 && x[2] == +1 ? "5" : "4");
} else { // x[0] == 0
switch (x[1] * 10 + x[2]) {
case 00: printf("%d\n", 8 - conc); break;
case 01: printf("%d\n", 7 - conc); break;
case 02: puts("6"); break;
case 11: puts("6"); break;
case 12: puts("5"); break;
case 22: puts("5"); break;
default: puts("> <");
}
}
} else puts("> <");
return 0;
}
933D - Оригинальное вырезание
Author skywalkert / Preparation skywalkert / Tutorial skywalkert
#include <bits/stdc++.h>
typedef long long LL;
const int mod = (int)1e9 + 7, inv2 = (mod + 1) / 2, inv3 = (mod + 1) / 3, inv5 = (mod * 2 + 1) / 5, inv7 = (mod + 1) / 7;
const int inv6 = (LL)inv2 * inv3 % mod, inv30 = (LL)inv5 * inv6 % mod, inv42 = (LL)inv6 * inv7 % mod;
const int coeff[4][8] = {
{0, 1}, // sum(b^0) = n
{0, inv6, inv2, inv3}, // sum(b^2) = 1/6 n + 1/2 n^2 + 1/3 n^3
{0, mod - inv30, 0, inv3, inv2, inv5}, // sum(b^4) = -1/30 n + 1/3 n^3 + 1/2 n^4 + 1/5 n^5
{0, inv42, 0, mod - inv6, 0, inv2, inv2, inv7} // sum(b^6) = 1/42 n - 1/6 n^3 + 1/2 n^5 + 1/2 n^6 + 1/7 n^7
};
LL n;
int f[4], g[4], ans;
int main() {
scanf("%lld", &n);
int nn = n % mod;
f[0] = nn * (nn + 1LL) % mod * (nn + 2) % mod;
f[1] = (3LL * nn + 4) % mod;
f[2] = mod - 3LL * (nn + 2) % mod;
f[3] = 2;
for(int x = 0; (LL)x * x <= n; ++x) {
LL rem = n - (LL)x * x;
int yLim = (int)ceil(sqrtl(rem));
for( ; (LL)yLim * yLim <= rem; ++yLim);
for( ; (LL)yLim * yLim > rem; --yLim);
int sum = 0, x2 = (LL)x * x % mod, x4 = (LL)x2 * x2 % mod, x6 = (LL)x2 * x4 % mod;
g[0] = (f[0] + (LL)f[1] * x2 + (LL)f[2] * x4 + (LL)f[3] * x6) % mod;
g[1] = (f[1] + 2LL * f[2] * x2 + 3LL * f[3] * x4) % mod;
g[2] = (f[2] + 3LL * f[3] * x2) % mod;
g[3] = f[3];
for(int i = 0; i < 4; ++i) {
int tmp = 0;
for(int j = i << 1 | 1; j >= 0; --j)
tmp = ((LL)tmp * yLim + coeff[i][j]) % mod;
sum = (sum + (LL)g[i] * (tmp << 1 | !i)) % mod;
}
x && (sum <<= 1) >= mod && (sum -= mod);
(ans += sum) >= mod && (ans -= mod);
}
ans = (LL)ans * inv6 % mod;
printf("%d\n", ans);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
#define re return
#define sz(a) (int)a.size()
#define mp(a, b) make_pair(a, b)
#define fi first
#define se second
#define re return
#define forn(i, n) for (int i = 0; i < int(n); i++)
#define bend(a) a.begin(),a.end()
typedef long long ll;
typedef vector<int> vi;
typedef pair<int, int> pii;
typedef pair<long long, long long> pll;
typedef long double ld;
typedef unsigned long long ull;
const ll mod = int(1e9) + 7;
ll n, sum1, sum2, sum3, sum4, ans;
vector<ll> cp;
ll mdd(ll c) {
c %= mod;
if (c < 0) c += mod;
re c;
}
ll pow1(ll k, ll st) {
ll ans = 1;
while (st) {
if (st & 1) ans = mdd(ans * k);
k = mdd(k * k);
st >>= 1;
}
re ans;
}
ll get_sum(ll n) {
n %= mod;
n += mod;
n %= mod;
re (n * (n + 1) / 2LL) % mod;
}
ll get_cnt(ll a) {
a = mdd(a);
re mdd(mdd(2LL * mdd(a * a) * a) - mdd(3LL * mdd(a * a) * mdd(n + 2)) + mdd(mdd(a) * mdd(3LL * n + 4)) + mdd(n) * mdd(mdd(mdd(n) * mdd(n)) + 3LL * n + 2LL));
}
int main() {
iostream::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (ll k = 1; k * k <= n; k++) {
ll c = mdd(k * k);
cp.push_back(k * k);
sum1 = mdd(sum1 + c);
sum2 = mdd(sum2 + mdd(c * c));
sum3 = mdd(sum3 + mdd(mdd(c * c) * c));
sum4 = mdd(sum4 + get_cnt(c));
//cout << sum4 << "\n";
}
ans = mdd(get_cnt(1) + 4LL * sum4);
ll k1 = 2, k2 = mdd(-3LL * (n + 2)), k3 = mdd(3LL * n + 4);
for (ll a = 0; ; a++){
while (sz(cp) && cp.back() + (a+1LL) * (a + 1LL) > n) {
ll c = mdd(cp.back() + a * a);
sum1 = mdd(sum1 - c);
sum2 = mdd(sum2 - mdd(c * c));
sum3 = mdd(sum3 - mdd(mdd(c * c) * c));
sum4 = mdd(sum4 - mdd(get_cnt(c)));
cp.pop_back();
continue;
}
if (sz(cp) == 0) break;
ll k = mdd(2LL * a + 1), ksq = mdd(k * k), ktr = mdd(ksq * k);
//cout << sum4 << "\n";
sum4 = mdd(sum4 + mdd(ll(sz(cp)) * mdd(k1 * ktr + k2 * ksq + k3 * k)) +
mdd(sum1 * mdd(2LL * k * k2 + 3LL * k1 * ksq)) +
mdd(sum2 * mdd(3LL * k * k1)));
//cout << sum4 << "\n";
ans = mdd(ans + 4LL * sum4);
sum3 = mdd(sum3 + mdd(ll(sz(cp)) * ktr) + mdd(sum2 * 3LL * k) + mdd(ksq * 3LL * sum1));
sum2 = mdd(sum2 + mdd(ll(sz(cp)) * ksq) + mdd(2LL * sum1 * k));
sum1 = mdd(sum1 + mdd(ll(sz(cp)) * k));
//cout << sum3 << " " << sum2 << " " << sum1 << "\n";
}
//cout << ans /6<< "\n";
ans = mdd(ans * pow1(6, mod - 2));
cout << ans;
}
933E - Важнейшее объединение
Author skywalkert / Preparation skywalkert / Tutorial skywalkert
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = (int)3e5 + 3;
int n, a[maxn], cnt, p[maxn], m, out[maxn];
LL f[maxn];
bool v[maxn];
int descension(int pos) {
int dt = min(a[pos], a[pos + 1]);
if(dt)
out[++m] = pos;
a[pos] -= dt;
a[pos + 1] -= dt;
return dt;
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%d", a + i);
LL odd = f[max(i - 2, 0)] + a[i], even = f[max(i - 3, 0)] + max(a[i - 1], a[i]);
f[i] = min(odd, even);
v[i] = f[i] != odd;
}
// a[n + 1] = 0;
LL ans = min(f[n - 1], f[n]);
// printf("%lld\n", ans);
for(int i = n - (ans == f[n - 1]); i > 0; i -= 2 + v[i])
p[++cnt] = i;
reverse(p + 1, p + cnt + 1);
for(int i = 1; i <= cnt; ++i) {
int pre = p[i - 1], cur = p[i], ctr = 0;
if(v[cur])
ctr += descension(cur - 1);
ctr += descension(pre + 1);
ctr += descension(cur);
assert(ctr == f[cur] - f[pre]);
}
printf("%d\n", m);
for(int i = 1; i <= m; ++i)
printf("%d\n", out[i]);
return 0;
}
Thank you everyone!
Happy Valentine's Day and happy Lunar New Year!










Auto comment: topic has been updated by Tommyr7 (previous revision, new revision, compare).
Please don't make problems that require either using python or programming your own BigInt class, It's unfair for people who exclusively program c++. I don't see any need for the bounds in div1B to be so large.
Or maybe I should just finally learn python...
Edit: I was wrong, the problem is definitely solvable with just long long. I'll do more research before complaining next time.
What? 35233893
do you think all these guys used their own BigInt class?
Feedback: Terrible pretests for D and terrible spj for E.
Oops... Sorry for the inconvenience. T_T
What is spj?
And I don't really think that pretests should be that strong. Yes, input is bigger than MOD, so you should be careful.
He means the checker. It is a pity that he operated on zeros and didn't pass pretests in problem E.
Ehem. It is written in bold that each operation should be on positive numbers.
Yes you are right. Maybe he is just too nervous with the end of the contest approaching :)
Terrible nickname.
Python2: 35268543
Perl: 35270787
python2 [42 bytes] : 35283953
Oh! It's so easy in python! Here is my C++ code: 35239158 (charlieshu is also me)
div1C: find all intersections -> build graph -> count edges and vertices -> F = 2 + E — V . Am I right?
Partially correct, think about three single circles.
Actually my tutorial is finished but it needs to be posted by the sleeping poster :(
Why is div1C = gym100200C ?
Auto comment: topic has been updated by Tommyr7 (previous revision, new revision, compare).
For Div1 C, it should be 3 if n=2 and two circles are neither intersect nor tangent
Thank you for pointing out. I will fix it later.
Auto comment: topic has been updated by Tommyr7 (previous revision, new revision, compare).
The tutorial isn't up for Div1A, and the code looks quite complicated. Here's a much simpler way:
Let's say we flipped a segment and found the best subsequence. It will look something like this: 11111122222222
Suppose we unflip the segment. Now the sequence looks like this: 1111222211112222
That is, it will be composed of 4 regions, made of 1s,2s,1s,2s. So the problem reduces to simply figuring out the longest subsequence of such form in the original sequence, no flipping necessary.
This can easily be done with a single O(N) traversal of the sequence. At each point, keep 4 values: the longest sequence of 1s, the longest sequence of 1s2s, the longest sequence of 1s2s1s, and finally the longest sequence of 1s2s1s2s.
EDIT: The editorial is up and they put this solution in it. Still, strange that they would use the complicated N^2 solution as the sample.
You Miss out cases like
111111122112211221122222221111
Here answer should be 18. It can be found if you twist from 7 index(0-based) to end.
Running it through my solution, I'm getting an answer of 24, so I think you're missing something. Flipping 7 index to the end does work for that (the only things missing from the increasing subsequence are the 3 pairs of 11 in the middle).
Thanks nice explanation it worked for me
Sir , I still didn't get why are we finding the longest subsequence of type 1s,2s,1s,2s in your solution.. Plz explain.
Because when you flip the middle segment of 2s and 1s, you get a sequence of 1s followed by 2s, which is what you want.
Is there still a O(n) solution if the sequence has more values(1,2,3,4,5...)?
Yes, your intuition is almost right.
In fact, a previous version limits 1 ≤ ai ≤ 5 and the author has tested a O(53n) solution :P
If in that case, we need to find out the longest subsequence of 1s5s4s3s2s1s5s, am I right?
Partially correct. There may be several cases such as 1-2-4-3-2-4-5.
Thanks a lot, and Happy lunar New Year!
Thanks a lot!
For the benefit of all beginners, here's my O(nm) solution for Div 2 A.
http://codeforces.com/contest/934/submission/35280443
My idea was to find all products, find the maximum product A[i]B[j] in one O(nm) scan.
Then, find the maximum without that particular A[i], in another O(nm) scan.
The best A can do is hide at most one element and A has to hide the element that contributes to the greatest product.
https://github.com/MathProgrammer/CodeForces/blob/master/Explanations/Explanations%2019/A%20Compatipble%20Pair%20Explanation.txt
This is exactly what I thought of except that I missed some corner cases and got WA :P. Nice approach !
Thank you !
Div 2- C/ Div-1 A:
I am unable to understand this case for which my solution is failing. The editorial is not yet there. Can anyone explain how is the answer to pretest 3 is 116. Many thanks :)
http://codeforces.com/contest/934/submission/35263594
Your answer of 13 is way too low.
My guess is that you interpreted "subsequence" to mean "subarray". The difference is that a subsequence doesn't have to be contiguous.
For example, 1 2 3 4 is a subsequence of 1 5 2 5 3 5 4.
Ah got it. Thanks. I read it wrong, my bad. Thanks for the help :)
My solution for "A Prosperous Lot" : 54 bytes. can we have a look at Tester Solution please.
n=int(input()) print(["8"*(n//2)+"9"*(n%2),-1][n>36])Not the best idea in E task. Complicated geometry that required special knowledges — it is not for 2-hour contest :(
Auto comment: topic has been updated by Tommyr7 (previous revision, new revision, compare).
Where is Div2D ? Edit: Sorry.
Can someone explain me div2 C?
Here is my approach. Ask me if you have any doubt.
Can someone explain another solution for problem
for Problem C, my solution is to regard each a[i] as the position changes from 1 to 2. That means, we calculate all 1's before i and all 2's after i, so we can get all maxium length through a[i] in O(n).
Then we do the reverse, we can regard the reverse section [L, R], only L < i < R will affect a[i]'s max length, and i split the section into two parts, [L, i) and (i, R]. For section [L, i] after reverse, we can minus all 1 and plus all 2 in the section. And for (i, R], it's simmilar but we plus all 1 and minus all 2.
Also, these two section are distinct, so we can get max L and R, sepeartely. Therefor the whole algorithm is in O(n^2)
Can someone explain to me why my solution for problem C in JAVA is giving TLE in large value of n. I am using similar approch as sak3t described in this comment. I see that c++ solution easily passes whereas Java is having a hard time.
Ideally it should pass the time limit easily. I don't find any bug in your submission. Probably it is some high Java intensive problem in your code.
PS: Try to optimize the code more. Like you don't need to store dp[i][j][k], as we need data for only dp[0][j][k] and dp[i][n - 1][k]. Notice, 0 and n - 1 constants. You can have this data in two linear arrays rather than one 2D array.
Thanks for the response. Check this solution. I thought that indexing may be an issue, so tried this way. And this amazing result :P
Woah, I had no idea, this can affect time taken by approximately 10 times.
Can anyone please provide beginner friendly explanation of Div2 E?
Can someone help me with my solution of DIV2 C. http://codeforces.com/contest/934/submission/35292502
In Problem A i just sorted the 2 arrays and the answer was the mutliplication of a[n-2]*b[m-1]
i skipped the max of tommy and get the max of banban * the max of tommy after deleting the it's first max and i got WA on test 10 any help please
Your code fail for this simple test:
3 3
-7 1 5
-7 1 5
so what should be the result 5 or 49
The correct answer is 25
How could I get the intersection of two circle, my previous method didn't provide enough precision.
I can't get the main idea behind quailty's method.
Could someone explain it for me?
For Div.1 D, there's a terrible mistake in the tutorial which almost drove me mad this morning and took me hours to realize what was wrong.
That polynomial of L mentioned in the tutorial appeared to be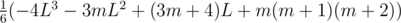 ,
,
but the correct polynomial seems to be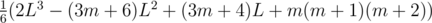 .
.
Please fix it as soon as possible!
Thanks so much! I also wasted a great deal of time on it.
Ha! You found a blind spot! The mistaken polynomial was from my draft paper (and I used to wrong profoundly...) but the standard solution uses the appropriate polynomial :P
The tutorial was fixed just now. Please wait for a while and refresh the page :)
Okay, thanks a lot. By the way, despite that accidental mistake, Div.1 D was really a wonderful and challenging problem :).
Many thanks Codeforces for the interesting problems.
RE: 933C - Цветное зрелище
Is there an explanation that the solution to test #115
3
0 0 1
0 3 2
4 0 3
is 5 not 4?
It seems that C1 = (0,0,1) is tangent to C2 = (0,3,2) at point P12 = (0,1), and is tangent to C3 = (4,0,3) at point P13 = (1,0). And, that C2 and C3 are not tangent and do not intersect. Therefore, the number of regions should be 4 not 5.
Thanks in advance for explaining.
Best wishes.
An update: A further analysis of the test case revealed that C2 and C3 are tangent at P23 = (8/5,9/5). Therefore, the area surrounded by the three arcs on C1, C2 and C3 extending between each pair of P12, P13, and P23 constitutes the fifth region.
Thanks again and best wishes.
can anyone please explain the approach behind div2A? I am not getting why do we need to print the minimum of maximums and not the 2nd maximum?
Please note tutorial for 933E has been revised for better understanding. Hope it will be helpful :)
For div2 E can anyone explain why is my algorithm wrong? Code
if n==1 , ans=2 ; if n==2 , ans=3 (two circle,universal region) , for every pair of circles intersecting:ans++ if n==3 , ans=4 (three circle,universal region), for every pair of circles intersecting: ans++. if all three intersects, ans++.
I cannot understand what is wrong with this algorithm? TIA.
You can use GeoGebra for reasoning. Here is test 14.
Can anyone please explain the question "A twisty movement" DIV2 C with this test case n=12: 1 2 1 2 1 2 1 2 1 2 Length of the Longest subsequence after the reversal is 8! Can anyone please tell [l,r] which need to flip to get this answer
Flipping [10, 11] gives 1, 2, 1, 2, 1, 2, 1, 2, 1, 1, 2, 2.
For 933 A, do not read the editorial's solution. It's, in simple words, bad. Use Um_nik's solution as well. Easy to understand.
How would you solve D1d's bonus? Sorry for necroposting but I can't find it anywhere.
I think it's similar to https://www.spoj.com/problems/DIVCNT1/
The solution uses Stern-Brocot Tree.