In case you want to take part in Yandex.Algorithm 2018 but somehow haven't registered yet, you might want to follow this link.
Qualification round has started at 00:00 Moscow time, February 17th. Round is a virtual competition 100 minutes long. You can start it at any moment of time till 23:59 on Sunday, February 18th (Moscow time).
We recall that in order to be able to participate in elimination stage one needs to accept at least one problem at qualification round. However, everyone who managed to accept at least one problem during warm-up has already qualified to the next stage.
Judges ask all the participant to withdraw from any problem discussion and do not publish any solutions till 01:40, February 19th.
Good luck, we hope that you will enjoy the problems!










Auto comment: topic has been translated by GlebsHP (original revision, translated revision, compare)
I really enjoyed the problems even if I couldn't solve a lot, very interested in the editorial :). Good job!
Please change English title to English. Because it is written in Russian I firstly ignored this.
Done, thanks
is it just me or it seems that the title is still not changed.
Haha, Gleb changed it to English title but in Russian language version, not in English :D
That just happened
Is there a way to end contest earlier if everything is already blind/AC?
I don't think so
Why do I have to wait something like 4 minutes for my submission to be included in standings? Is it like that in further rounds as well?
We are working on this issue. Hope that during Qualification this is not critical.
It was happening during entire Petrozavodsk camp, so I think that it's problem with whole yandex system.
Why are u always complaining btw
6 hours remaining before end of qualification round. Hurry up! :)
I don't get it, is there any advantage to submitting blind??
Submitting blind reduces penalty time (which is irrelevant in qualification round)
01:40, February 19th Moscow time has passed. How to solve F?
Suppose minimal such distance is d. Then we can place servers on the diameter in vertices that are at distance d from diameter ends. Now we can just binary search for d
Is there a way to solve this if the number of servers > 2?
I do not see easy way to generalize this solution
Alternative approach.
Fix d and root the tree. Take a look at node v with maximum depth. For covering it, there should be a server somewhere in subtree of d-th parent of v, say u. With greedy conclusions it's optimal to set one of the servers exactly in u.
Then choose v as the deepest node from the set of nodes uncovered by the first server (it can be disconnected but it doesn't matter) and set the second server in the d-th parent of new v.
Now check whether each node is covered.
Seems to be generalizable for > 2 servers
If you can solve this problem: https://main.edu.pl/en/archive/oi/16/gas, then you can enlarge the number of servers a little.(I guess...)
My solution seems to work in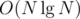 with arbitrarily number of server.
with arbitrarily number of server.
First binary search the farthest distance d. For a fixed d, I'm going to find the least possible number of servers to cover all vertices within d. Let dp[i] be the critical vertex in the subtree of vertex i, where critical vertex is the deepest one still uncovered, if all the vertice in the subtree of i are covered, the critical vertex is the highest one placed with server.
Then, for each vertex i, collect critical points from its direct children. If the critical point is placed with server but farther than d, skip it. For those uncovered critical points, keep the deepest one. For those with server, keep the highest one. Considering following cases:
Then, I can find the least possible number of servers to cover all vertices within d.
It's somehow greddy and I didn't prove it.
Find center of tree. Then cut the deepest or second deepest subtree, find diameter of each component is also pass.
Centre is defined as midpoint of any diameter. I don't have a formal proof for it, but it works. Intuitively, since we can prove centre is unique, it makes sense for it to be answer for a single server.
Also can be easily generalised for an arbitrary K number of servers since at each step, you find diameters of each tree(of the forest) in total O(N) time, so solution is overall O(N·K).
Wow,your solution is cool,but could you tell me about if you should choose 3 nodes,how to proof that your solution is still correct.And I don't know well how to divide the diameter.
I think the 3 server nodes would be the original tree center, and the 2 centers of the partitioned trees. I don’t have a way to prove/test it, but it seems somewhat intuitive by the same arguments as for 1 or 2 servers.
However, now that you mention it, I believe it is non-trivial to extend this for more than 3 nodes, possibly just doing a greedy(choosing node that minimizes current answer most) works, but I can see why it might not.
Nope:
The only optimal solution for three servers is 2, 3, 4, but the center is 1.
How to solve E?
Use 2 pointers to find, for each left index, the rightmost right index such that all words are covered
How to solve D?
If we want the smallest possible sequence which we cannot form a triangle, it will be Fibonacci sequence. consider at most the first 100 numbers in a range, because Fibonacci numbers get larger.
Wow that's an easy solution.
I solved it with two pointers and sets to find dp[L] which gives you the leftmost right border so that this interval havs a valid triangle .. and then in the quereies I see if dp[L]<=R and I print the triple .. and it passed :D .. I don't think the writera meant my solution.
How did you calculate dp[L] ?
you keep moving with the right pointer until you have found a triangle ... but how know that you found one?
You have two sets, one for the lengths of the current interval, and one for saving the 3 indices that form a triangle (there may be more than one triple).
Then when you move one step to the right you add this length to the lengths set and you see it's neighbors one to the right, one to the left, two to the right and two to the left and try to form triangle with them. If some triple forms a triangle you add it to the second set with the minimum index first to sort them by index.
So when the second set is not empty that means that you have found a triple so you can stop, and by that you have found the leftmost R that you can form a triangle with.
I think we can improve a bit this approach. We can store only one triangle and there is always be R index. When move left border we must check only existence triangle with R (if one of the indexes was L). If no such triangle move R.
I learned this idea from the editorial of 766B.
But we should get first 100 sorted elements in range [L;R] (using segment tree for example), isn't it?
you don't have to, for each query sort the first min(100, size) elements in temporary array.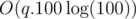 , it's fast enough to pass the time limit.
, it's fast enough to pass the time limit.
I tried to make up antitest and understood what did you mean :D
Nice idea.
i have 2 questions on yesterday's yandex. 1: can some one plz give me a proof for why this solution for c works. https://ide.geeksforgeeks.org/dkwmWVvF88
2: And i used segment tree for d in which i find the 3 maximum elements in a segment. And if those 3 cant form a triangle, print -1. But it doesnt work. failure on last test case. here is the code https://ide.geeksforgeeks.org/KsnMcNWu6K
2: How did you decide that choosing the largest 3 elements will be sufficient?
Counter-case 3,4,5,10
For C, the answer is n^((n-1)^2) because after you fill the top-left (n-1)x(n-1) submatrix with anything, there is exactly one way to fill the remaining cells so that the matrix is valid.
Can you proof that the rightest lower cell would be always correct ? UPD: oh, i understood why is it works )
can you elaborate it
1) Consider the top-left (n-1)x(n-1) submatrix 2) The sum of right column will be equal of sum of those elements plus the rightest lower cell 3) The sum of the bottom row will be equal the same => exactly one way to fill value to the last cell.
how do you say that there exists one way. why cant you have 0 ways?. no number to fill it. cuz these 2 sequences are entirely different and how adding those integers will give the same number modulo n.
We should proof, that sum of bottom row is equal to sum elements of right column.
an, 1 + an, 2 + ... + an, n ≡ a1, n + ... + an, n (n), we can sub from both sums an, n
Let's proof it.
=> they both contain top-left (n-1)x(n-1) submatrix => the sums are equals => there's exist a value for an, n
Another way to explain: you can fill all cells except for main diagonal with any values. After that you can set the desired values to the main diagonal elements.
UPD. This solution is wrong. But it led me to a correct formula due to the double mistake. Thanks God, I'm an idiot!
main diagonal?
for all cells except the both diagonals, doesn't it?
I don't think either idea works, you can't fill center in these cases for N=3
[_,1,1] [1,_,1] [1,2,_]or[_,1,_] [1,_,1] [_,2,_]Any ideas why my solution of problem D gets WA on first test (though it passes the samples)? https://pastebin.com/iiMfq5fJ Maybe I misunderstood something
Successful hacking attempt of Stroustrup's solution.
Thanks a lot, I see now, something went terribly wrong with my two pointers approach