959A - Махмуд, Эхаб и игра в четное-нечетное
It's easy to see that if n = 0, the next player loses. If n is even, Mahmoud will choose a = n and win. Otherwise, Mahmoud will have to choose a < n. n is odd and a is even, so n - a is odd. Ehab will then subtract it all and win. Therefore, if n is even Mahmoud wins. Otherwise, Ehab wins. n = 1 doesn't follow our proof, yet Ehab still wins at it because Mahmoud won't be even able to choose a.
Code link (me) : https://pastebin.com/X3D08tg9
Code link (mahmoudbadawy) : https://pastebin.com/4u3RHE7n
Time complexity : O(1).
Bonus task : If there were multiple integers, and each player can choose which integer to subtract from, who will win?
959B - Махмуд, Эхаб и сообщение
It's easy to see that for every word, the minimum cost of sending it is the minimum cost of sending any word in its group. For each group, we'll maintain the minimum cost for sending a word in it (let it be costi) and for each word, we'll maintain its group (let it be groupi). For every word i in the message, we'll add costgroupi to the answer.
Code link (me) : https://pastebin.com/3RFeEkgD
Code link (mahmoudbadawy) : https://pastebin.com/sR5eZy7d
Time complexity : O((n + m)log(n) * len).
Bonus task : Try to solve the problem if the input was given as pairs of words that are synonyms (assuming synonymy is transitive).
959C - Махмуд, Эхаб и неправильный алгоритм
The first tree
For n ≥ 6, you can connect nodes 2, 3, and 4 to node 1 and connect the rest of the nodes to node 2. The real vertex cover is the set {1, 2} of size 2 while the found vertex cover will have size min(3, n - 3). As n ≥ 6, that value will be 3 which is incorrect.
For n < 6, the answer doesn't exist.
The second tree
There are multiple ways to construct it. One easy way is the star tree. Connect all the nodes to node 1. The real and the found vertex cover will be simply {1}. Another easy way is a path. Connect node i to node i + 1 for all 1 ≤ i < n. The real and the found vertex cover has size 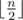 .
.
Code link (me) : https://pastebin.com/7J8B9fXx
Code link (mahmoudbadawy) : https://pastebin.com/54jZ8sGM
Time complexity : O(n).
Bonus task : Try to find an elegant proof that the answer for n < 6 doesn't exist for the first tree.
959D - Махмуд, Эхаб и еще одна игра про построение массива
Common things : Let's call a number "ok" if it could be inserted to array b, as a new element, without breaking any of the conditions (i.e it should be coprime with all the previously inserted elements). Let's call the maximum number that could be inserted in the worst case mx. For each integer from 2 to mx, we'll precompute its prime divisors with sieve.
First solution by me
Create an std::set that contains all the numbers from 2 to mx. That set has all the "ok" numbers and will be updated each time we insert a new element to array b. We'll insert the elements to array b greedily one by one. At index i, let cur be the minimum number in the set greater than or equal to ai i.e std::lower_bound(a[i]). If cur isn't equal to ai, the lexicographically greater condition is satisfied and we're no longer restricted to a, so, starting from index i + 1, we'll greedily choose cur to be the first (minimum) number in the set instead. We'll insert cur to b. Each time, we'll remove all the integers that aren't coprime with cur from the set. To do that, we'll loop over the multiples of its precomputed prime divisors and remove them from the set.
Code link (me) : https://pastebin.com/bg3Hi6r2
Second solution by KAN
Let used[i] indicate whether some prime is already a factor of one of elements in b (so we shouldn't use it). Each time we insert an element to b, we update used by iterating over its precomputed prime divisors and make them all used. We'll start inserting elements to b greedily one by one. To check if a number is "ok", we'll iterate over its precomputed prime divisors and check that all of them aren't used. While ai is "ok", we'll keep inserting it to b. We'll reach an integer that isn't "ok". In this case, we'll iterate naiively until we find an integer that is "ok" and insert it to b. The lexicographically greater condition is now satisfied and we can insert whatever we want (no restriction to a). Notice that starting from now, b will be sorted in increasing order. That's because if it's not, we can sort it and reach a better answer without breaking any of the conditions. The naiive solution is to loop starting from 2 until we find an "ok" integer for each i. However, as the array is sorted, we can loop starting from 2 the first time and then loop starting from bi - 1 + 1 and save a lot of loops that we're sure will fail!
Code link (me) : https://pastebin.com/Xh2QgqUf
Time complexity : O(mxlog(mx)). mx has an order of 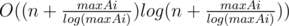 because the nth prime is expected to be O(nlog(n)) and the number of primes less that n is expected to be
because the nth prime is expected to be O(nlog(n)) and the number of primes less that n is expected to be 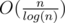 .
.
959E - Махмуд, Эхаб, исключащее ИЛИ и минимальное остовное дерево
For convenience, let n be the label of the last node not the number of nodes (i.e n = ninput - 1).
Denote lsb(x) = x&( - x) as the value of the least significant bit set to 1 in x. The answer is 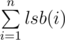 , which means that node u is connected to node
, which means that node u is connected to node 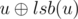 for all 1 ≤ u ≤ n (node u is connected to node u without that bit).
for all 1 ≤ u ≤ n (node u is connected to node u without that bit).
Now let's see how to calculate that quickly.
Math solution
Let f(x) be the number of integers y such that 1 ≤ y ≤ n and lsb(y) = x, then 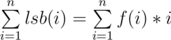 . f(i) > 0 if and only if i is a power of 2 so this sum is equivalent to
. f(i) > 0 if and only if i is a power of 2 so this sum is equivalent to 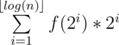 . Basically, the first number y such that lsb(y) = x is x and then the period is 2 * x. Take 4 to see that. The integers y such that lsb(y) = 4 are {4, 12, 20, 28, etc.} Therefore,
. Basically, the first number y such that lsb(y) = x is x and then the period is 2 * x. Take 4 to see that. The integers y such that lsb(y) = 4 are {4, 12, 20, 28, etc.} Therefore, 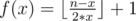 for 1 ≤ x ≤ n and x is a power of 2.
for 1 ≤ x ≤ n and x is a power of 2.
Code link (me) : https://pastebin.com/dNuR9k0Y
DP solution
Let's see how the sequence of lsb(x) is constructed. We start with {1} and at the ith step, we copy the sequence and concatenate it to itself and add 2i in the middle.
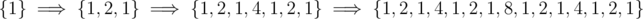
Let 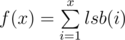 . Let dp[i] = f(2i - 1).
. Let dp[i] = f(2i - 1).
You can see from the pattern above that dp[i] = 2 * dp[i - 1] + 2i - 1 for 1 < i (with the base case that dp[1] = 1). Let's find a recurrence for f(x). Denote msb(x) as the value of the most significant bit set to 1. The sum can be split into 2 parts : the sum from 1 to msb(x) and the sum from msb(x) + 1 to x. You can see that in the second sum, lsb(i) can never be equal to msb(x), so we can remove that bit safely without affecting the answer. Removing that bit is like xoring with msb(x) which makes the sum start at 1 and end at 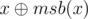 which is
which is 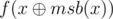 . Therefore,
. Therefore, 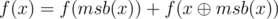 . The first part can be calculated with the help of our dp because msb(x) is a power of 2 and the second part goes recursively. Basically, for each i such that the ith bit is set to 1, we add dp[i] + 2i to the answer.
. The first part can be calculated with the help of our dp because msb(x) is a power of 2 and the second part goes recursively. Basically, for each i such that the ith bit is set to 1, we add dp[i] + 2i to the answer.
Code link (me) : https://pastebin.com/wnhBZx2v
Time complexity : O(log(n)).
959F - Махмуд, Эхаб и ещё одна задача про исключающее ИЛИ
Let's solve a simpler version of the problem. Assume the queries only ask you to see whether the answer is 0 or positive instead of the exact answer. We can answer all the queries offline. We can keep a set containing all the possible xors of subsequences and update it for each prefix. Initially, the set contains only 0 (the xor of the empty subsequence). For each index i in the array, we can update the set by adding  to the set for all x in the set. The intuition behind it is that there's a subsequence with xor equal to x (as x is in the set) and if we add ai to it, its xor will be
to the set for all x in the set. The intuition behind it is that there's a subsequence with xor equal to x (as x is in the set) and if we add ai to it, its xor will be  , so we should add it to the set. That's a slow solution to update the set, but we have some observations:-
, so we should add it to the set. That's a slow solution to update the set, but we have some observations:-
- If x is in the set and y is in the set,
 must be in the set. To see that, let x be the xor of some elements and y be the xor of other elements.
must be in the set. To see that, let x be the xor of some elements and y be the xor of other elements.  must be the xor of the non-common elements (because the common elements will annihilate) so it must be in the set.
must be the xor of the non-common elements (because the common elements will annihilate) so it must be in the set. - If x is in the set and y isn't in the set,
 can't be in the set. This could be proved by contradiction. Assume
can't be in the set. This could be proved by contradiction. Assume  is in the set, then, by the first observation,
is in the set, then, by the first observation, 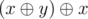 must be in the set. This is equivalent to y which we said that it isn't in the set. Therefore,
must be in the set. This is equivalent to y which we said that it isn't in the set. Therefore,  isn't in the set.
isn't in the set.
Basically, if ai is already in the set, we do nothing because updating the set would do nothing but extra operations according to the first observation, and if ai isn't in the set, we don't even waste a single operation without extending the set! That makes the total complexity O(n + maxAi) or O((n + maxAi)log(maxAi)) depending on implementation because each element is added to the set exactly once.
To solve our problem, let's see the naiive dynamic programming solution. Let dp[i][x] be the number of subsequences of the first i elements with xor x. 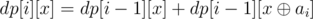 . The intuition behind it is exactly the same as the intuition behind the set construction. Let's prove that dp[i][x] is equal for all x belonging to the set! Let's assume this holds true for i - 1 and see what happens in the transition to i. Notice that it holds true for i = 0. Let j be the value that dp[i - 1][x] is equal to for all x belonging to the set. If ai is in the set, and x is in the set,
. The intuition behind it is exactly the same as the intuition behind the set construction. Let's prove that dp[i][x] is equal for all x belonging to the set! Let's assume this holds true for i - 1 and see what happens in the transition to i. Notice that it holds true for i = 0. Let j be the value that dp[i - 1][x] is equal to for all x belonging to the set. If ai is in the set, and x is in the set,  is in the set (observation #1). Therefore, dp[i - 1][x] = j and
is in the set (observation #1). Therefore, dp[i - 1][x] = j and 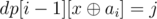 which makes dp[i][x] = 2 * j for all x in the set. Notice that the set doesn't change so dp[i][x] = 0 for all x that aren't in the set. If ai isn't in the set, we have 3 cases for x. If x is in the set,
which makes dp[i][x] = 2 * j for all x in the set. Notice that the set doesn't change so dp[i][x] = 0 for all x that aren't in the set. If ai isn't in the set, we have 3 cases for x. If x is in the set,  isn't in the set. Therefore, dp[i][x] = j + 0 = j. If x is to be added to the set in this step,
isn't in the set. Therefore, dp[i][x] = j + 0 = j. If x is to be added to the set in this step,  is in the set. Therefore, dp[i][x] = 0 + j = j. Otherwise, dp[i][x] = 0. To summarize, we'll maintain the set. For each integer, if it's in the set, we'll just multiply j by 2. Otherwise, we'll update the set. We'll then answer all the queries for that prefix (saying 0 or j) depending on whether x is in the set.
is in the set. Therefore, dp[i][x] = 0 + j = j. Otherwise, dp[i][x] = 0. To summarize, we'll maintain the set. For each integer, if it's in the set, we'll just multiply j by 2. Otherwise, we'll update the set. We'll then answer all the queries for that prefix (saying 0 or j) depending on whether x is in the set.
Code link (me) : https://pastebin.com/Kfi0NWTi
Time complexity : O(n + maxAi) if you implement the "set" with a vector and an array.
Bonus task : Can you make this solution work online? Can you do that with maxAi < 230?



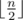 . Second, the found vertex cover is also at most
. Second, the found vertex cover is also at most 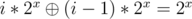 because
because 






Can someone pls give the proof asked in bonus task of problem C?
Let x be the correct answer to the problem. (optimal answer). Let y be the result of the described algorithm.
Because x is the optimal and y is the greedy solution, x <= y holds.
For x = 1, it's a star graph. So the described algorithm works.
For x >= 2,
what does problem div 2 C means? i already read the problem 10 times
An alternative solution for E:
Write any reasonable algorithm for MST (Kruskal for example), simulate it for n = 2,3,..10 (build a clique for each such n with weights as described in the statement). It should give a sequence of MST weights: 1,3,4,8,9,11,12,20,21. Put this sequence into oeis.org and implement the recursive formula it gives.
First, the formula is the same as my formula.
Second, this is not a good practice because you didn't prove the solution and didn't benefit from the problem.
I didn't say it's any kind of recommended solution. It's just an alternative, not mathy, not dp, just another approach passing the tests.
Isn't it a way to practice one of possible (and not so uncommon) ways to solve a problem during contest?
how do you get formula from oeis?
implement brute , then copy paste the result for n <= 10 or 15 into the oeis search bar , and then when you find the sequence look down below , in the 'formula' section!
i can't make any sense of this
G.f.: 1/x/(1-x) * (x/(1-x) + Sum(k>=1, 2^(k-1)*x^2^k/(1-x^2^k)))
Not this one, the one just below it for a(n)
Can you elaborate on it little more?
f.society
So, call solve(n-1) after getting the input. [First part of the formula]
Hope this helps!
thank you very much
nothing wrong with using oeis during contest imho as long as after contest participant tries to prove the solution formally , like the saying goes , a man's gotta do what a man's gotta do
Alternative solution for F (and bonus task F):
Interpret integers as 30-dimensional vectors of integers modulo 2 (then xor is addition). Incrementally process each prefix of the array with Gaussian Elimination, which will give you ≤ 30 basis vectors. To answer the query (l, x), see if x can be expressed through basis vectors for prefix l, if no then the answer if zero, otherwise it's pow(2, l-number_of_basis_vectors). Since there cannot be more than 30 basis vectors, they won't change more than 30 times as you process the prefixes. You can remember all those ≤ 30 sets of basis vectors to answer queries online. Complexity: O((n+q)*log(maxAi)).
Your complexity is O((n + q)log2(maxA)).
I used this ideia with complexity O(n + q)log(maxAi).
I stand corrected, But since xor'ing ints is so fast it makes sense to think of the complexity as about (n+q)*30 operations.
Maybe it's late in the evening, but I got something wrong about the algo.
Let's imagine all a[i]=same value=x Then answer is (2^l)-1. Rather than 2^(l-1)
In D, it would be better to just iterate for primes once the lexicographically greater condition is met.
36912822 why memory limit exceeded in this code ? where can be the problem ?
You swapped m and k.
For n<=5, the vertex cover found has size at most 5/2, that is, at most 2. The only way this vertex cover is not the minimum vertex cover is when the algorithm finds 2 as the answer, while the actual answer is 1. But the only way for the answer to be 1 is if the tree is a star. If the central vertex is the root, then evenCnt=1, and if some leaf is the root, then oddCnt=1. Either way, we get a contradiction.
For E I thought the recurrence on OEIS was much simpler
http://oeis.org/A006520
b(n-1) is the answer where b(x) can be defined
In main function shouldn't b(n+1) (as given on oeis) be called instead of b(n-1) as in your submission??
I came up with the recurrence by looking at that, but my base case is different / the problem is not exactly the same.
You can see ans(n+1) = a(n) = b(n+1)
so ans(n) = b(n)
but with base can b(0) = 0, we get b(1) = 1
This means b(x) will calculate cost of xor-mst with x edges as opposed to x vertices.
Tree with n vertices is defined as having n-1 edges. Therefore b(n-1).
Hi, I'm a contest contestant: Codeforces Round # 473 (Div. 2)
there was a code that was not tested and was sent during the contest; is the problem D, since the problem I sent remained in Pretests passed, but when I sent it after the answer the contest answer gave me correct answer
This is my code during the contest: http://codeforces.com/contest/959/submission/36929338
This is my code after the contest: http://codeforces.com/contest/959/submission/36933508
both are the same code
Why i am getting MLE??
http://codeforces.com/contest/959/submission/36935187
Because you are using too much memory.
Look at fun() again then analyze the complexity.
I did same as author's code.i think it's okay!!
d[j].push_back(i); p[i]=true;
is actually supposed to be
d[j].push_back(i); p[j]=true;
This makes the function use much more memory and time than it's supposed to (n log n vs n log log n).
In problem D, why I change the position of two sentences, the judge results differ?
the first one got AC 36938566
and the second one got Runtime error 36938574
Can someone help me?
In the wrong code you are keeping an iterator of the set then by calling solve() function you are making some changes in the set which changes the structure. Your iterator might have been changed when you are trying to check if it is larger then a[i].
Oh, many thanks!
Could someone share the teste code for the problem C:
Here is my submission http://codeforces.com/contest/959/submission/36925494
For section 1, I set the root at 1 and n/2 children for 1 and all the other children for node 2. This is a valid solution because nodes 1,2 is enough for vertex cover. But WA for N=99. I have been checking for a while unless I am missing something.
Your idea for section 1 is correct. Nevertheless section 2 is incorrect. The first two cases are small, but for bigger cases your approach is incorrect. You build a tree in which every node has two children, and sometimes the algorithm described in the description gives an incorrect answer. You can try N=10, in which your tree gets 5 as an answer, but can be done with 4. There are better ways to solve section 2, like a line, or a star-tree
what does problem div 2 C means? i already read the problem 10 times
Please help with problem D, as to where my logic is wrong?
My code — http://codeforces.com/contest/959/submission/36939522
Your approach is incorrect. The correct answer is not always the nearest prime. Try this test: 2 10 20 Your Answer: 10 23 Correct Answer: 10 21 Here, 21 is correct because 7 and 3 are still available, and it is a valid solution, smaller than yours.
One thing I really like about your editorials is that you give us code links to study as well :)
Here is my solution and my explanation to D. It's the same idea as Kan's. But I think mine will be easier for a beginner to understand.
I solved F online code. my solution is going to work for bonus task as well
Problem.C n=8 why cant the answer be 1-2 2-3 3-4...7-8 for the first section? even depth 1,3,5,7 odd depth 2,4,6,8 min()=4 ,but choose(2,5,8) node=3
According to your solution, you missed the edges:{3,4},{6,7}
Thanks...it seen I misunderstood the statement
How to calculate mx in Question D?
My java solution was giving tle for test 6 when I took mx= 2000005 as in the solution of the problem setter,but by hit and trial I got to mx= 1500005 which got AC.
Thanks for an interesting round. The logic and intuition behind problem E seems to be very interesting however, many people are discussing that the pattern was available on OEIS. Being a pupil I just want to know how top programmers solve such kind of problem during the contest. So, I am writing 2 comments to get a poll. Please read the comment below. Thanks :)
Upvote this comment if you used the trick of generating answers for small values of N and then searched for the pattern on OEIS.
Else upvote this comment if you actually arrived at the formula using intuition and some thinking.
The solution to Bonus F is quite different from the solution to F, and for that reason I believe it should be put in the editorial.
It's not a small twist on the approach we're using. Gaussian elimination is quite a different approach and I'd love for the editorialist mohammedehab2002 to include this in the editorial so that we can understand it.
Otherwise, it's a very good editorial.
I'll add the solutions of all the bonus tasks to the editorial. I'm just leaving some time and space for the contestants to share their thoughts.
UPD added them.
Hey mohammedehab2002, just wanted to say that I solved problems after the contest and I felt they were super cool :) Thanks
My code for question B is giving TLE. Can someone help me out?
http://codeforces.com/contest/959/submission/37004683
You mixed k and m. See the order of input data. I changed it and got
AC.submission
Problem F was just awesome. Also, the bonus task, maxAi < 2^30. Learned a lot, thanks!!
Tutorial of problem F is very good. Didn't see the "All number in the set have the same number of subgroups! Also enjoyed the Bonus task! It's a nice thing to add :)
For problem D, how do you know it is bounded by 2000005? I tried to put the 1e5th prime + 1 as the bound (1299710) but it fails.
We can assume that the worst case is that you'll add n primes and all of them are greater than maxAi so you can bound it to the 105 - th prime greater than 105. The worst case is even much better than that. Anyway, the worst case I could find is bounded to less than 14 * 105.
So, did you find the 105 th prime greater than 105 ? What will be the general strategy to find a good upper bound in problems like these ?
what does problem div 2 C means? i already read the problem 10 times
If anyone requires further explanation for the beautiful solution to Problem D, I have written an extensive explanation on Quora here. If you have doubts, feel free to discuss :)
Can anyone tell me why in problem D.Mahmoud and Ehab and another array construction task it gives TLE in TEST 1 with Java 46461498 but it was accepted with C++ 46461449 ?
Super easy online solution for F with xor basis: 73340139
I am not able to understand the proof of problem E. Please help. :(