How inclusion exclusion is related with Mobius function ? In F.Relatively Prime Powers judge solution with Mobius function.
Can anyone help me get the trick for this problem with Mobius function ?
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 152 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
How inclusion exclusion is related with Mobius function ? In F.Relatively Prime Powers judge solution with Mobius function.
Can anyone help me get the trick for this problem with Mobius function ?
| Name |
|---|



In this problem, we know how to count the number of integers from 2 to n having gcd of ki divisible by some number x (that is just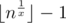 , since we have exactly this number of integers not less than 2 that can be raised to x-th power without exceeding n), but we need to count the number of integers having this gcd exactly equal to 1.
, since we have exactly this number of integers not less than 2 that can be raised to x-th power without exceeding n), but we need to count the number of integers having this gcd exactly equal to 1.
How would we handle this with usual inclusion-exclusion? Let S be some set of prime numbers, and f(S) be the product of primes from S (if S is empty, then f(S) = 1), then the answer would be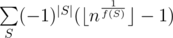 by inclusion-exclusion formula. Note that in previous formula we are summing up these values over all possible sets of prime numbers S — and since we have infinitely many prime numbers, the number of possible sets S is also infinite.
by inclusion-exclusion formula. Note that in previous formula we are summing up these values over all possible sets of prime numbers S — and since we have infinitely many prime numbers, the number of possible sets S is also infinite.
However, we know that for sufficiently large x (in the case of this problem, for something like x > 60, but typically we can apply this technique even if the border is somewhere at 106) the number of integers such that gcd of their ki is divisible by x becomes 0 (because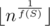 quickly becomes equal to 1). And that is what gives us an opportunity to apply Mobius function.
quickly becomes equal to 1). And that is what gives us an opportunity to apply Mobius function.
In the formula listed above, we iterated over sets of primes. Let's have it backwards: we will iterate on the integer x, and for each such integer try to count the number of sets having f(S) = x, and the number of primes in these sets.
If the factorization of x contains some prime number twice (or even more than twice), then there is no such set of prime numbers S such that f(S) = x. Otherwise, there is exactly one such set S which is equal to the factorization of x; and if the factorization contains even number of primes, then ( - 1)|S| = 1, otherwise ( - 1)|S| = - 1.
And now we can actually see that the previous two sentences are actually very close to the definition of Mobius function! If the factorization of x contains some prime twice or more, then μ (x) = 0, otherwise if the number of primes in the factorization of x is odd, then μ (x) = - 1, and if it is even, then μ (x) = 1. This actually allows us to rewrite the formula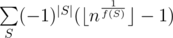 in a more calculatable way:
in a more calculatable way: 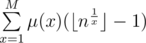 , where M is some constant after which all the summands become equal to 0 (in this problem M is somewhere close to 60).
, where M is some constant after which all the summands become equal to 0 (in this problem M is somewhere close to 60).
If there are some questions, I can try to elaborate a bit more. In fact, we gave some other problems using this technique on previous Educational Rounds, so you can try solving them to understand it better: 915G 803F 920G
BledDest Thanks for explanation.
I don't understand why that summation over all possible sets of prime numbers gives us what we want.
Actually i have two problems here:
why summing over sets of prime numbers?
Assuming first problem is solved, why does this summation gives us total number of numbers with power's gcd of one? i mean why one?
What would i get by doing as you explained if i define S over just some limited selected primes like {2, 3, 11}?
I figured this out by thinking about inclusion/exclusion more precisely. If this helps others having the same problem as mine.