Hi all,
Today I'd like to present you yet another suffix data structure. According to my (quite limited) knowledge, it is new. But even if it's not, I believe the data structure possesses such a clarity that it is hard to screw up its implementation. So I think it might be interesting to a competitive programmer.
This is a byproduct of my attempt to find a simple solution for the problem of real-time indexing. Today we won't care for real-time part, thus hash-tables and amortized algorithms are welcome to keep things simple. All code snippets are in Java.
Definitions
I assume you are familiar with strings, substrings, prefixes, suffixes and so on. Just to be safe:
- A suffix of string ω is called “proper” if it is not ω itself. For example, empty string is a proper suffix of any non-empty string; ω is the longest proper suffix of cω for any character c.
- A string π has an occurrence in ω if it contains π as a substring. There might be more than one occurrences of π in ω. We’re particularly interested in the leftmost occurrence (LMO). For example, empty string’s leftmost occurrence is before first character of any non-empty string.
- Every non-leftmost occurrence will be either called repeat or said to be repeating. For example, longest repeating suffix (LRS) of ω is always a proper suffix of ω; empty string has no LRS.
- Characters of strings are indexed from 1.
The data structure
The data structure is built in online fashion. For each prefix of the input string it calculates longest repeating suffix (leftmost occurrence of it, to be precise).
Each leftmost occurrence is identified by its right end (inclusive) and length. This we can denote with an ordered pair of two numbers.
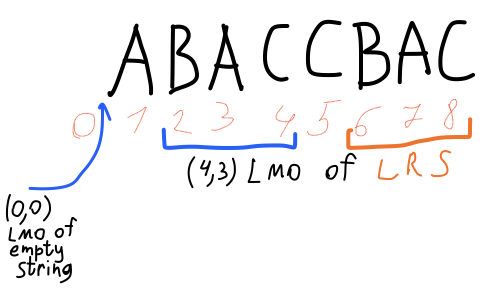
There are three components in the whole structure:
- String
- LRS array, which stores LMO of LRS of every prefix of the string.
- Hash-table
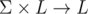 that given LMO of π and character c returns LMO of π c (an extension of π with c).
that given LMO of π and character c returns LMO of π c (an extension of π with c).
The hash-table stores only non-trivial extensions. (An extension is trivial if it is yielded by simple increments of the length and the right end.)
It might look in Java as follows:
List<Character> text;
List<Lmo> lrs;
Map<Pair<Character, Lmo>, Lmo> extensions;
LMO operations
This is not strictly necessary, but we’ll define null as a character that is equal to any other. This will allow us to avoid corner cases in the algorithm later.
boolean isNext(Character c) {
Character next = text.get(rightEnd + 1);
return next == null || next.equals(c);
}
For LMO extension there are two cases: trivial and from extensions table.
boolean hasExtension(Character c) {
return isNext(c) || extensions.containsKey(Pair.of(c, this));
}
If next character of LMO is c, then trivial extension is LMO as well. Proof: if any other occurrence were leftmost, it would contradict the premise.
Lmo extend(Character c) {
return isNext(c)
? new Lmo(rightEnd + 1, length + 1)
: extensions.get(Pair.of(c, this));
}
Longest proper suffix of LMO is too having two cases: trivial and when it coincides with corresponding LRS. In the latter case you must take corresponding LMO. Proof: by definition, LRS is a repeat and thus cannot be LMO. Trivial case is proven by contradiction.
Lmo lrs() {
return lrs.get(rightEnd);
}
Lmo longestProperSuffix() {
return length - 1 == lrs().length
? lrs()
: new Lmo(rightEnd, length - 1);
}
Computing LMO of LRS
Now, given we implemented Lmo class with all operations and made it hashable, we are ready to construct the LRS array.
The algorithm belongs to the same party, where you can find Knuth, Morris, Pratt, Ukkonen and droptable all hanging around. These algorithms are online and maintain longest suffix for which some particular invariant holds. Our case is closest to Ukkonen’s: we maintain the longest suffix which has already occurred earlier.
We take LMO of LRS and try to extend it with c. If it fails, we store the newly found LMO and try to extend the shorter suffix. The algorithm runs in amortized (expected due to hash-table) O(1) for the same reason other similar algorithms do.
As I said earlier, empty string has no LRS. To avoid this corner case we use standard trick. We allow empty string to have artificial LRS such that:
- It is extendable by any character.
- It extends to empty string.
This we achieve by placing at 0 index of the string null character and stating that zeroth element of LRS array is ( - 1, - 1).
Algorithm to compute LRS when appended new character c looks literally like this:
Lmo longest = lrs.get(lastIndex);
while (!longest.hasExtension(c))
{
extensions.put
(
Pair.of(c, longest),
new Lmo(lastIndex + 1, longest.length + 1)
);
longest = longest.longestProperSuffix();
}
longest = longest.extend(c);
Now, some problems to solve with this algorithm.
Counting distinct substrings
If after appending new character the string is n characters long, then n new substrings has appeared save repeating ones. Thus total amount of distinct substrings of n-characters string is:
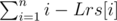
Problem to solve: Timus. 1590. Bacon’s Cipher
Longest common substring
Add first string, then some special character. Then append characters from the second string and output the maximum LRS. But you must ignore those with LMO in the range of second string.
Problem to solve: Timus. 1517. Freedom of Choice
Counting repeats
You can process LRS array to build tree of repeats, by inverting the array. You should walk this tree and compute number of repeats for each length. Then you need to account them cumulatively: if there are several repeats with the same right end, shorter ones are sub-repeats of longer ones.

Problem to solve: 802I - Fake News (hard). Advice: make Lmo comparable.
Building sorted suffix list online (right-to-left)
Not sure why do this, but anyway.
If you look at the string from right to left, every LRS becomes LCP. This means that this algorithm gives you the neighbor of each new suffix (UPD: not exactly, see below) and a way to compare them in constant time. Thus you have an insertion point for every new suffix.
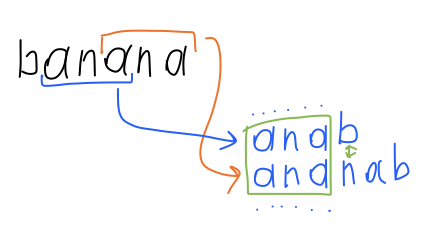
Suffix reported by LRS might be size-of-alphabet apart from its insertion point. To find true neighbor you have to either:
- provide random access to the list and perform binary search
- or construct additional map
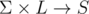 that says for each LMO π and character c where to find a suffix of form α cπ. This map must be ordered, so you can find closest c.
that says for each LMO π and character c where to find a suffix of form α cπ. This map must be ordered, so you can find closest c.










