Hello friends!

This weekend, on 8-9th of December — St. Petersburg, Barnaul, Kremenchug, Tbilisi, Almaty and Sochi will host the XIX Russia Team Open High School Programming Contest. Competition will be attended by more than 250 teams. Contest is held for the first time in Sochi this year -Educational Center “Sirius” will host nine teams.
The main contest will start on 9th of December at 10:00. You can follow current results by the link. Link to the tasks will be able right after the start of the tour.
A mirror will be available on Dec/09/2018 11:05 (Moscow time) – this is for those, who are not a participant, but also want to solve interesting problems! Do not join our broadcasts if you plan to take a part in the mirror. We warn you that, because of spoilers. And, of course, do not open the problem conditions before the start of the round.
If you do not want to participate in a mirror, be sure to join our broadcasts — in video format from the ICPCLive team and in text format in our Telegram-channel!
And if you want to come to the Russia Team High School Contest in St. Petersburg as a guest – just fill in the guest form and get your badge at the registration!
Our friend ismagilov.code has a post – follow this link to see a large set of commands with their total rating. Thank you for interesting information!
And please welcome some teams that stand a good chance to become Cup winners:
| Team | City | Participant 1 | Participant 2 | Participant 3 | Rating |
| Мертвые души | Kazan + SPb | scanhex | 300iq | Крамник Сергей | 5641 |
| Вова спит дома | Moscow | voidmax | Aleksandr2754 | Jatana | 6854 |
| Чудо Зверята! | Almaty | YaKon4ick | 998kover | ruslanjan | 6727 |
| danya.smelskiy | Kremenchuk | Sonechko | MaxZubec | Nazikk | 6701 |
| Проблемы с Поллардом? | SPb, Vsevolozhsk | kkarnauk | receed | forestryks | 6660 |
| Komarovi+Mziuri 1 | Tbilisi | saba2000 | Temotoloraia | baqargam | 6597 |
| Пурпурный виноград | Moscow | cookiedoth | Kuyan | TheWayISteppedOutTheCar | 6558 |
| Пыльная Испания | Chelyabinsk | Mlxa | sava-cska | liriKl | 6529 |















It's gonna be cool^^
What is testcase 2 in problem Minimal product
In F How to prove solution is always unique given you ask all nC3 queries.
You can ask all 10 queries for 5 elements of the array. Let those element in sorted order be a,b,c,d,e. Let xi be sum of returned values in all queries in which ith element was involved. Sort them, Then, you can form 5 linear equations using the returned values.(6e+3a+2b+c=x5, 3e+3d+3a+2b+c=x4, 3e+2d+2c+3a+2b=x3, 3a+3b+3e+2d+c=x2, 6a+3e+2d+c=x1) If you solve those linear equations their solution is always unique for any xi. Thus, we can uniquely determine these 5 elements. Similarly, thus you can uniquely determine all of the elements for the constraints(n>=5).
My solution with precomputed inverse matrix of above linear equations 46821561
How to solve Problem I Minimal product
You are given an array of size N, now your task is two find two indices i and j such that i < j, A[i] < A[j], and A[i] * A[j] is as minimal as possible across all possible valid pairs. Since an O(N²) solution is straight forward, we will discuss how to solve this in O(N).
The final state of the answer is dependent on whether the answer is positive or negative, so we will split the answer in three cases, and solve individually for each.
Answer is negative, so A[i] * A[j] < 0 for optimally chosen i, and j. In this case, it is easy to solve as only one element can be negative, which follows that it must be A[i], since A[i] < A[j] from the problem conditions. Solving this is simple, we need to maintain a prefix minimum across all the array, then for every element A[i], it can contribute to the above case iff prefix_minimum[i] * A[i] < 0, then for all valid indices, we need to minimize the answer over prefix_minimum[i] * A[i], where prefix_min[i] is equal to minimum(prefix_minimum[i — 1], A[i]).
This case is easy to solve as well, for each element we just need to minimize over A[i] * prefix_min[i], if A[i] > prefix_min[i].
This is really the interesting case, since both numbers are negative, we should greedily try to multiply numbers with minimum absolute value. For example, multiplying -3 by -2, is more beneficial than say, multiplying -20 and -25, even though -3, and -2 are larger numbers. This makes the greedy approach used in case #1, and #2 fail to arrive at an optimal solution.
Let’s try to come with another strategy, we can notice that once a negative number A[j] appears in the array, it will never be beneficial to pair any element less than A[j] at position < j, with any element after j. More formally, Let’s denote our indices as i, j, and k, where i < j < k, A[i] < A[j], and A[i], A[j], A[k] < 0. Then, A[k] * A[j] < A[i] * A[k] for all k.
In another words, we should try and match each index with every non matched yet index to it’s left that is less than it. At first sight, this looks like O(N²), but with careful implementation we can achieve O(N) in amortized time. We will be using a monotone stack ( a stack where every value is increasing from bottom to top). Before we push an element to the stack, we keep popping every element less than it, and minimize over this pair, otherwise we stop, and push that element. We are essentially simulating the idea in the previous paragraph. This is a smart brute-force that combines greedy to only iterate over possibly interesting pairs.
Here’s a snippet: https://ideone.com/FxK16x
You still have to construct the array using a generator, here’s a spoiler on how to do it efficiently, you can use an unsigned int data type for your array.
Problem I: unsigned int l and r (very stupid mistake (must be int)) and O(N2) solution passes 12 test cases...
Is this a coincidence or on purpose?
Why is it not possible to submit in practice mode? I wasn't registered for the round.
When will the solutions become available?
How to solve L?
Let's make a function f(x) that will tell us how many lections we can provide for each student in group of x students.
One of the possible optimal schedule patterns is greedy: fill empty slot in it with the number of student with least lections attended. Consider x = 6, n = 5, a = 5, b = 3: schedule is:
This way each student attends at least 3 lections. So f(6) = 3 in this case. We can show that result of this function is equal to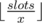 , where slots is the sum of students capacity over all days. Note, that in case when a > x or b > x we cannot put more than x students in one day. So the final formula is:
, where slots is the sum of students capacity over all days. Note, that in case when a > x or b > x we cannot put more than x students in one day. So the final formula is:
This function is monotonic. f(v) ≤ f(u) for v > u. Now we can make a binary search over x to find maximum amount of students that each student can attend at least k lections.
Thanks, that helps a lot!
Thanks for this
Can you please provide an editorial?
In question I Minimal product the array b has to be declared as unsigned long long
How to solve problem J? Definitely brute force isn't gonna work.
Can anyone explain why my hash code can't get through the test set 12 in problem K even though I have changed the hash value so many time ? Is it some kind of ati-hash test or something ? I changed the code to store the whole string and it got AC.
AC code : 46843561
WA code : 46843449
Can someone explain their approach for J?
I will use zero-based half-interval indexing.
You need to find the number of redundant pairs (c, d), 1 ≤ c ≤ |s|, 1 ≤ d ≤ |t|. We'll call such a pair redundant if there exists a pair (a, b), 1 ≤ a ≤ |s|, 1 ≤ b ≤ |t| such that s[0, a) + t[0, b) = s[0, c) + t[0, d) and a < c, here + is string concatenation. The final solution is then |s||t| - r, where r is the number of redundant pairs.
By means of simple algebra we can transform the previous string equality to:
t[0, b) = s[a, c) + t[0, d)
or equivalently, taking 1 ≤ x = c - a:
t[0, d + x) = s[a, a + x) + t[0, d)
t[0, x) + t[x, x + d) = s[a, a + x) + t[0, d)
Let z be the result of the z-algorithm on t. For each x > 0, z[x] is the largest value of d such that t[x, x + d) = t[0, d). So, for the above equality to hold, we must have d ≤ z[x] and s[a, a + x) = t[0, x). In other words, for each nonempty prefix of t, we will find all of its occurrences in s, that is, indices a such that s[a, a + x) = t[0, x) except those where a = 0. For each such occurrence, we need to put a marker on (a + x, d) saying that this pair is now redundant. Actually, we've shown that if (c, d) is redundant, then (c, d') will also be redundant, where d' < d, so, for each c we only need to store the largest value of d such that (c, d) is redundant.
Computing this in almost linear time is the tricky part. Build the suffix automaton on s[1, |s|) that is, without the first letter. We're omitting the first letter because we must have a ≥ 1. Let Ax be the set of all a + x such that s[a, a + x) = t[0, x). This set corresponds to the state of the automaton reached when you start from the root and follow the path t[0, x). Since we're processing prefixes of t in increasing order, we can easily find all these states. Into each state we can write the maximum value of the z-function z[x]. Now, we will max-propagate these values along inverted suffix links. Since Ax corresponds to a set of substrings of s, this corresponds to propagating the max value from these substrings to all states which contain larger substrings whose suffixes are Ax. Think of this as expanding these substrings to the left. Finally, for each state of the automaton which corresponds to a prefix s[0, c) of s (c ≥ 1), we will read the maximum value of d, and summing these d values will give us the required number of redundant pairs.
Code: 46835810
why my O(n) solution is giving tle on testcase 13. code — https://codeforces.com/contest/1090/submission/46848255
Here's a puzzle for you: try to find the difference: 46856549 and then explain why this is significantly faster.
The only difference is making mod1 const , i tried to search about it and i found since we cant change the value of a const so compiler can perform optimised operations and since i am using mod1 many times in my code , so overall it makes a significant difference . Although i am not completely sure thats the reason ..
That's correct! And yes, it can make a big difference.
Where can I see the editorial for the problems?
https://neerc.ifmo.ru/school/archive/2018-2019/ru-olymp-team-russia-2018-presentation.pdf