If the single 1 is located on the intersection of the r-th row and the c-th column (1-based numeration), then the answer is |3 - r| + |3 - c|.
If k > n, then the answer doesn't exist. Otherwise let's sort the squares by descending of their sizes. Now you can print any point that belongs to the k-th square and doesn't belong to the k + 1-th square. One of the possible answers is (ak, 0).
First of all, we have to check that each number occurs in the input exactly 4 times. If it's not true, then the answer definitely doesn't exist.
Otherwise, let's try to restore the circle. As cyclic shift of circle doesn't matter, let 1 to be the first number. As the second and the third number must be connected to each other and to 1, there are only few possibilities. So let's try them all. And when we know first three numbers, the rest of the circle could be easily and unambiguously restored in O(n). Just find a number, which is not included in the circle yet, and is connected to the last two numbers of the circle. Add this number to the resulting circle (as new last number), and repeat the procedure while possible. If we succeeded to add all the numbers to the circle, than the resulting circle is the answer.
Consider any simple path v1, v2, ..., vr which cannot be increased immediately (by adding a node to it's end, vr). In other words, all the neighbours of vr are already included in the path. Let's find the first node of the path (say, vl), which is connected to vr. It is clear that vl, vl + 1, ..., vr is a cycle and it contains all the neighbours of vr. But according to the problem's statement, each node has at least k neighbours. So length of the cycle is at least k + 1 ( + 1 is for node vr itself).
Divide the rhombus of size k into 4 right-angled triangles as shown on a picture below. One of them has size k, two — size k - 1, and another one — size k - 2.
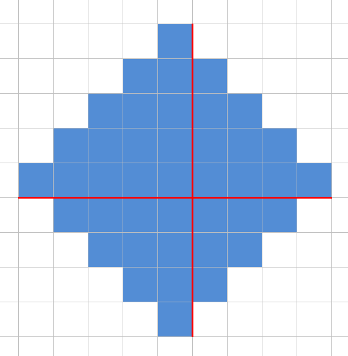
Let's solve the problem separately for each triangle. The most convenient way to do that is to rotate the input 4 times and run the same solving function 4 times. The result of this function will be a 2D array. Cell (x, y) indicates the answer we get if the right-angled vertex of triangle is located at cell (x, y). So it will be easy to combine 4 such arrays (just rotating and shifting properly) to get the actual answer for rhombus.
The main idea of the solution for triangle is the following. If we know the answer for a cell, we can easily move our triangle by one cell in any direction (right, down, left, or up) and recalculate the answer for that new cell in constant time. In fact, we need only 2 directions: right and down. And the values for top left corner should be calculated with straightforward cycles in O(k2) time.
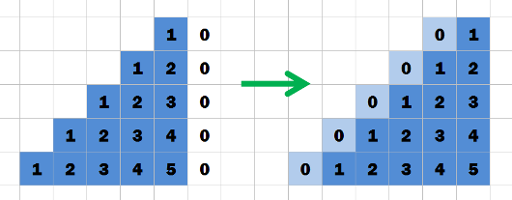
More precisely, let's define 5 functions:
The sum on diagonal segment of k elements:
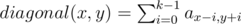
The sum on vertical segment of k elements:
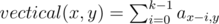
The weighted sum on vertical segment of k elements:
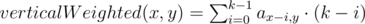
The sum on a triangle:
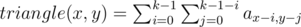
The weighted sum on a triangle:
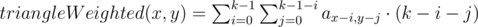
Calculating the first 3 functions in O(nm) in total is quite obvious. Formulas for the others are following:
triangle(x, y + 1) = triangle(x, y) - diagonal(x, y - k + 1) + vertical(x, y + 1)
triangleWeighted(x, y + 1) = triangleWeighted(x, y) - triangle(x, y) + verticalWeighted(x, y + 1)
Formulas for moving in other directions are similar.











You also need to mention that, for 263C - Circle of Numbers, how: - N=5 is trivial (any combination works) - N=6 there are 12/(6C2=)15 possible pairs, so ensure that the missing 3 pairs are not neighbours - N>6 probably your approach will work (N>=10 would be safest)
and also, please clarify what you mean by
..., there are only few possibilities. So let's try them all...For example, for N=1, say i discover that 1 is neighbours to 6 and 3, and 6 and 3 are neighbours to each other, it could be '1 (either 3 or 6) (either 3 or 6) ...' or '(either 3 or 6) 1 (either 3 or 6)...' What are you trying to say? maybe illustrate with a link to a AC submission, please.much appreciated.
Let's consider the number of the common neighbours of 1 and 3(say,t1) and the number of the common neighbours of 1 and 6(say,t2).
If t1=2 and t2=1, then it should be 1 3 6.
If t1=1 and t2=2, then it should be 1 6 3.
If t1=2 and t2=2, then it should be 3 1 6.
[deleted]
+1 for the tutorial! I hope that all next contests will have a similar one! And nice contest by the way :)
My solution to problem C is quite different from the tutorial:
Triangle means: for an edge(u, v), there exists k that both edge(u, k) && edge(k, v) exist.
Special cases should be noted: the given graph may not be connected!
I don't get it, why N = 6 is special case, can someone point it out please?
Actually I make use of this property: If N >= 7, then for three consecutive vertices (a, b, c), a will be connected with (d, e) and c will be connected with (f, g), and (d, e, f, g) will be distinct vertices. For N == 6, this property does not hold.
Thank you.
No problem :)
For N>=7, nodes X and Y are next to each other in the circle iff their adjacency lists look like this:
X(A,B,Y,E1) Y(A,B,X,E2)
where E1 != E2.
for special case, if each point is exactly connected to 4 other points and there're 2*n nodes, the whole graph must be connected
Do you mean 2n edges? Consider this case: put two valid n=5 cases together to get an n=10 case, this graph is disconnected but all nodes is connected with 4 other nodes.
It was really unfair not to rejudge problem D as many clearly wrong solutions passed(see this thread) and thus decreased the point of the problem. My solution may fail too in rejudge but fair result should be ensured.
take vertex = 1 + ( n * m + ( n ^ m ) + ( n & m ) + ( n | m ) ) % n; find max distance to all its neighbour, get accepted what is logic to solve it?
Does anybody have an idea for the problem E ?
I have wrote a solution in Chinese, anyone can view it. here is my blog
Here is my approach for case N = 6 in problem C:
Because each node connects to exactly 4 others, there're always 3 pairs of nodes which are not neighbors. Find these 3 pairs and put them into the circle. Place node a of pair (a, b) in any position i from 1 to 3 (make sure it's still available), then place node b in position i + 3.
I wonder why I got TLE in Div1.C by not checking if all numbers are repeated 4 times... It doesn't change the order, does it?
can someone please explain me that why we use |3-x| + |3 — y| in beautiful matrix
The problem asks to move the only '1' to the center of the matrix, which is located as (3, 3). For any position with (x, y), we need |x-3| + |y-3| steps to move it to the center. You may refer to Manhattan Distance for more details, and if you still have questions, welcome to discuss.
i am getting tle my code is for beautiful matrix question``
include include using namespace std;
int main() { int arr [5][5]; int x,y =0; for (int i = 1; i <=5; i++) { for (int j = 1; j <= 5; j++) { cin>>arr[i][j]; if (arr[i][j]== 1) { x =i ; y =j ;
} } } cout<<(abs(3-x)+abs(3-y)); return 0; } please help me out
If you use arr[5][5], then both i and j should not exceed 4. In other words, when i=5 or j=5, it leads to out of bound. You may use arr[6][6] instead.
why be have to take arr[6][6] as when we have to define an array we define it by its size ie is 5x5
The index in general starts from 0, and thus for arr[5], we could only use arr[0], arr[1],...,arr[4]
if i run my code in code editor for test case 1 . it give me correct output .but when i submit this code .they give me output 7 .why and what is the wrong
include<bits/stdc++.h>
using namespace std; int main() { ios_base::sync_with_stdio(false); cin.tie(NULL); int arr[5][5]={0}; for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { cin>>arr[i][j]; }
} if(arr[2][2]==1) { cout<<"0\n"; return 0; } int move=1; int x,y; for(int i=0;i<5;i++) { for(int j=0;j<5;j++) { if(arr[i][j]==1) { x=i; break; } else move++; } if(x==i) break; // cout<<endl; }// cout<<move<<endl;
int cnt=0; for(int i=move;i<13;i++) { cnt++; } cout<<cnt<<endl; return 0;}
A pretty neat trick for Problem A.