In various places(12), people have talked about "Dinic's With Scaling" having $$$O(VElog(U))$$$ complexity, where U is the max edge capacity. However, in just as many places, people have cast doubt about this complexity or worried that this algorithm ends up being slower in practice(12).
I had the same doubts. In fact, a couple months ago I benchmarked Dinic's with scaling on some hard test cases and thought that Dinic's with/without scaling performed similarly.
As it turns out, I benchmarked it again yesterday and found that Dinic's with scaling definitely has significantly better asymptotic complexity (by a factor of V).
Synthetic Benchmarking
I used the hard test case generator at 2 posted by ko_osaga here. The one posted at 1 creates a graph with only V edges and moreover, doesn't work for me... Notably, given a V, it generates a graph with V nodes and $$$O(V^2)$$$ edges.
The code I used was my own Dinic's implementation (originally from emaxx) found here. Notably, the SCALING variable toggles between Dinic's with scaling and without. It's a small change, as you can see.
I ran the two code across a variety of input sizes, averaging across 10 runs, then taking the log of input size and times, plotting them in a 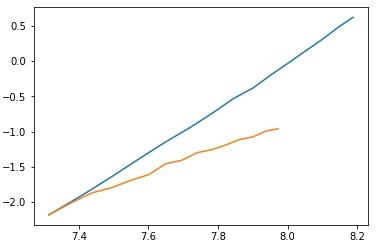 where blue is the runtime of Dinic's without scaling and orange is the runtime of Dinic's with scaling. Since the important thing to look at is the slope of the line, I normalized the lines to start at the same point.
where blue is the runtime of Dinic's without scaling and orange is the runtime of Dinic's with scaling. Since the important thing to look at is the slope of the line, I normalized the lines to start at the same point.
Fitting a linear regression to the points, we see that the slope of Dinic's without scaling is 3.204, while the slope of Dinic's with scaling is 1.93, which correspond to complexities of $$$O(V^3)$$$ and $$$O(V^2)$$$ respectively.
In terms of actual runtime, here are some numbers on specific sizes.
Benchmarking on Problems
There are 3 flow problems, I benchmarked on — SPOJ FASTFLOW, (VNSPOJ FASTFLOW)[https://vn.spoj.com/problems/FFLOW/), and a Chinese LOJ Flow Problem (it's intended to solve this problem with Highest Label Preflow Push, which has $$$O(V^2\sqrt{E})$$$ complexity).
Also, to vouch for my implementation, here's some benchmarks with other implementations :^) Mine (to enable scaling change the SCALING boolean), Emaxxs dinic,LOJ fastest (HLPP, the fastest submission on the Chinese flow problem). As I was doing these benchmarks I realized the LOJ submission is actually faster than mine on all of my benchmarks :'(. It is substantially longer than my implementation though :^)
SPOJ (V<=5000, E<=3e4)
Mine: 0.04
Emaxx Dinic: 0.11
Mine w/ scaling: 0.27
LOJ fastest: 0.00
VNSPOJ (V<=5000, E<=3e4, harder test cases):
Mine: TLE
Emaxx dinic: TLE
Mine w/ scaling: 0.00
LOJ fastest: 0.00
LOJ (V<=1200, E<=120000):
Mine: 56 points
Mine w/ scaling: 88 points
Emaxx dinic: 44 points
LOJ fastest: AC, 1176 ms total, #1 on leaderboard
Synthetic Test(N=2000, E=4e6):
Mine: 66.56
Emaxx dinic: 247.40
Mine w/ scaling: 0.14
LOJ fastest: 0.10
Number of non-whitespace characters:
Mine: 1164
Emaxx dinic: 1326
LOJ fastest: 2228
Conclusions:
First off, HLPP seems to be superior to Dinic's in terms of runtime, so perhaps the real lesson is that people should be using HLPP. Also, I hope to provide a solid well-tested implementation of Dinic's with scaling that people can use. Other than that, however, I hope it's clear that Dinic's with scaling really does have a significant improvement in runtime (approximately a factor of V), and that translates to significantly better performance on real problems.
PS: If anyone has a flow implementation they think is better than mine, I'd like to see it :^)










Auto comment: topic has been updated by Chilli (previous revision, new revision, compare).
I've just been made aware of dacin21'simplementation, and although I haven't had the time to properly compare it yet — it does seem to be fairly fast — 0.05 on SPOJ, 0.03 on VNSPOJ, and 2000 ms on LOJ. It also seems to be reasonably short — seems very impressive.
It's not really my own implementation, I think I got it from the kactl codebook. If I recall correctly, the only thing I changed in this version was fixing a runtime error when the source node is isolated. (I also have a modified version of it for fast bipartite matching.)
I'll try some of my other codes on the LOJ problem and see how they fare. (I couldn't really benchmark on the SPOJ problem anymore, as the runtime were really low. Moving to static memory allocation reduces the runtime from $$$0.05$$$ to $$$0.02$$$ for example. I didn't want to do that in my codebook for obvious reasons.)
Kactl notebook truly is a gold mine of great implementations...
Does push-relabel provide a noticeable speed improvement in bipartite matching over Hopcroft-Karp?
From my experience (from a few problems I solved) it does, although I have never benchmarked it (I never wrote Hopcroft-Karp actually). My $$$0.00$$$ on https://www.spoj.com/problems/MATCHING/ uses Push-Relabel.
One thing to note for matching problem is that you should pick the vertex with the lowest label to discharge (for flow you pick the one with the highest label) and do global relabeling, both to get the theoretical $$$O(\sqrt{V} E)$$$ bound and for it to run fast in practice. There were also quite a few constant-factor optimizations, such as keeping all the excess on one side of the graph.
Do you have a source for the fact that "lowest global relabel" gives $$$O(\sqrt{V}E)$$$? I couldn't find anything from the google search I just did.
Just found it on a comment from Dacin21: https://codeforces.com/blog/entry/58048?#comment-417654
nice
The LOJ submissions was really interesting to have a look at. Here's my quick analysis of it:
With the improved gap relabeling, I now also got my $$$0.00$$$ on SPOJ, but getting that is rather inconsistent (I submitted a few times and the runtime varied between $$$0.00$$$, $$$0.01$$$ and $$$0.02$$$.)
Thanks for the analysis of that implementation! I've noticed that for my implementation of Dinic's, storing the edges in a 2d adjacency list performs better than in a flat structure.
The single global relabeling is interesting too — I've always thought it was something you do repeatedly. Is there any way to test its performance without that single global relabeling at the beginning? Removing it for me causes the code to fail.
Yeah, running global updates every $$$\sim 4 n$$$ relabels is what the papers suggest. With some heuristics in the global relabeling, I got the following runtimes on LOJ (SPOJ is still $$$0.00$$$) (with static memory)
$$$\require{siunitx}$$$
so it does indeed help. I also tried partial augmentation, but that was a lot slower. (Maybe I understood it wrong, the notes about it "The Partial Augment-Relabel Algorithm for the Maximum Flow Problem" are a bit vague about the multi-push operation.)
Well, I get slightly less drastic results, but it does seem to be superior to do global updates every $$$4n$$$ relabels. One note, I'm counting each gap relabel as multiple relabels, while you seem to count them as just one — counting them as multiple relabels seems to help for me.
With global updates, I get a best of $$$913$$$ ms, and with only an initial update, I get a best of $$$1050$$$ ms.
If anyone wants to use the really fast implementation from LOJ in their library, I simplified it and cleaned up some stuff here: https://gist.github.com/Chillee/ad2110fc17af453fb6fc3357a78cfd28#file-hlpp-cpp
It's currently the fastest/tied for 0.00 seconds on all 3 of SPOJ FASTFLOW, VNSPOJ FASTFLOW, and LOJ flow.
It comes in at 87 lines and 1687 non whitespace characters, so decently long, but about 30% shorter than the original implementation and a lot easier to understand for me.
There is an error in the code. In line 41, you try to get the back element from an empty queue.
Well... Perhaps undefined behavior is the correct word. At least in my compiler (gcc c++14), it returns a reference to the last element that was in the queue.
I do agree that it's pretty jank(and should be changed), but it's not an "error".
Sorry, I meant undefined behavior too. It surprisingly doesn't work on my compiler and gives a runtime error.
Alright, I fixed it. Thanks for pointing out that it fails.
In line 50 of your dinic with scaling implementation:
for (lim = SCALING ? (1 << 30) : 1; lim > 0; lim >>= 1)If capacity is long long, is
1 << 30enough? Shouldn't it be higher, like1 << 62?as capacity scaling says "the highest bit of max capacity".
Hi, thanks for the nice implementation first! In SPOJ, I use my java version based on your hlpp code, and I got a rte(nzec). And when i use 2 * MAXN to create these arrays and vectors then I got an ac. So can you show your spoj submission? I want to check whether there are errors in my java implementation.
Sure. https://ideone.com/j7H5nD
Seems maxV + 5 will solve this issue. Thanks for sharing.
Hi, I think you have made a mistake in testing ko_osaga's synthetic test. I think that test is made for source = 1 and sink = n, maybe you tested for some other source or sink. Your dinic with scaling takes quite a lot of time in that case. Even for N = 1000, M = 1e6, it takes 3.5 second on ideone: https://ideone.com/vh6Uxm
Chilli Hi, I believe your github HLPP code fails on the following test case: https://ideone.com/HbPNMR
The correct answer is 40000024.
Found a simpler test case
The correct answer is 2, but the github HLPP outputs 1.
One really weird thing is that the directed edge 8->3 really shouldn't matter, but removing it somehow makes HLPP find the correct max flow.