The starting position can be anywhere with a footprint. The footprints can be categorized into 3 types.
- only L s
- only R s
- R s followed by L s
In case 1, we end in the left of all footprints. In case 2, we end in the right of all footprints. In case 3, we either end in the rightmost R or the leftmost L
We can simply move by greedy method — only moves when it takes the boat closer to the destination.
Obv 1: If a has odd parity, we can apply operation 1 to increase its number of 1s by 1.
Obv 2: If a has even parity, its number of 1s cannot increase anymore.
Claim: If the number of 1s in a is not fewer than those in b, we can always turn a to b
The idea is to make a copy of b at the right of a. Lets assume a starts with even parity. If we need a 0, simply apply operation 1. If we need a 1, keep remove from the head until we removed an 1. Notice that we never remove digits from 'new part' of a. Now the parity of a will be odd and we can apply operation 1. After that, the parity of a becomes even again, the number of 1 in the 'old part' of a decrease by 1 and we handle a 1 in b. Finally, remove the remaining old part of a and we get b.
Combine all those facts, we can conclude that we can turn a into b if and only if
First we sort a and b in non-increasing order. We claim that the answer is YES if and only if exists a is lexicographically larger than b.
 If a is not lexicographcally larger than b, that means for every i, ai ≤ bi. That implies for every fish Alice has, there is a corresponding fish Bob has and is as heavy as Alice's.
If a is not lexicographcally larger than b, that means for every i, ai ≤ bi. That implies for every fish Alice has, there is a corresponding fish Bob has and is as heavy as Alice's.
 Let i be the smallest index such that ai > bi. We can amplify the gap between wai and wbi as large as we want to make Alice wins.
Let i be the smallest index such that ai > bi. We can amplify the gap between wai and wbi as large as we want to make Alice wins.
297C - Splitting the Uniqueness
An equivalent definition for almost unique, is an array with at least ⌊ 2n / 3⌋ different elements. The idea is to split s into three parts: In the first part, we give uniqueness to a. In the second part, we give uniqueness to b. In the third part, we give uniqueness to both.
Lets assume s is sorted. Since s is an unique array, we know si ≥ i for all i (0-based). The image below will give some intuition on how we are going to split it. a is red, b is blue, the length of the bar represent the magnitude of the number. In the first and second part, we do not care about the array that we are not giving uniqueness to.
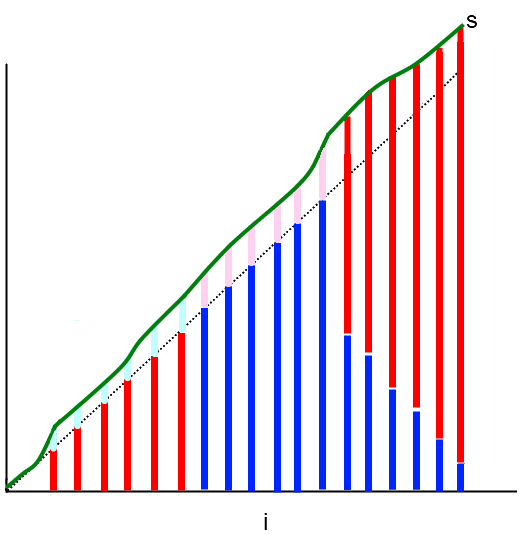
For exampmle, if n = 30:
i = 0... 9: assign ai = i (do not care values of b)
i = 10... 19: assign bi = i (do not care values of a)
i = 20... 29: assign bi = 29 - i and set ai = si - bi. From i = 20, a will have strictly increasing values starting from at least 11.
For k = 1 there is only one coloring so we just need to check the number of = constraints. When k ≥ 2, it turns out that using only 2 colors is always sufficient to satisfy at least 3 / 4 of the constraints.
Lets assume w ≥ h (rotate if not). We will call the constraints that involves cells in different row "vertical constraints", and similar for "horizontal constraints".
First we color the first row such that all horizontal constraints in row 1 are satisfied. We will color the remaining rows one by one.
To color row i, first we color it such that all horizontal constraints in row i are satisfied. Then consider the vertical constraints between row i and row i - 1. Count the number of satisfied and unsatisfied vertical constraints. If there are more unsatisfied constraints than satisfied constraints, flip the coloring of row i. Flipping a row means turning 2211212 → 1122121, for example.
If we flip the coloring of row i, all horizontal constraints in row i are still satisfied, but for the vertical constraints between row i and row i - 1, satisfied will turn to unsatisfied, unsatisfied will turn to satisfied. Therefore, we can always satisfy at least half the vertical constraints between row i and row i - 1.
The number of unsatisfied constraints is at most (h - 1) × ⌊ w / 2⌋, which is at most 1 / 4 of the total number of constraints (recall w ≥ h).
Problem and editorial written by AEtheReal. Link to editorial.











"If n > m, we can increase every wi for sufficient amount and done, because Alice always gains more than Bob." This sounds unclear to me. I would just say that we can set all w_i to be equal to 1 and then Alice wins.
Oh, that's a simpler argument! Do you mind if I put in in the editorial?
How could I mind, go ahead.
Could you tell me how did you invent problem Div1-C? I mean where did the idea come from? :) It should be interesting! :D
Actually it does not come from real life problem. I was thinking to make a problem about splitting, and I came up this.
Oh :)
I really liked the idea :)
"(=>) Let i be the smallest one such that a_i > b_i. We can amplify the gap between w_a_i and w_b_i large enough to make Alice win."
Would it also be correct to say make w_a_i much larger than w_b_i and make w_x = w_a_i for any x > a_i, so that the rest of the terms cancel each other out?
Yes
div2-E and div1-D are awesome.
This contest is more about idea rather than code ability. I love it actually though code ability is poor.
And this place sounds unclear to me. There is not exactly one more vertical constraints than horizontal: there is w - h more vertical constraints. And I don't understand what are you talking about in following statement, in fact we have already satisfied 75% of constraints (of course if h ≤ w).
Yeah, i also think so. The number of vertical constraints is (h — 1) * w = hw — w, and the number of horizontal constraints is (w — 1) * h = hw — h. In this solution, You have already satisfied all horizonal constraints and half of the others. So, if w >= h, You have already solved the problem.
Ya, I mean, if we only consider the constraints "settled" after filling the i-th row, it may be less than 3/4. I was hopping to explain how to come up the idea of "W >= H", instead of writing "if H > W swap them" in the beginning of the solution, which may be confused "how do you come up this?"
1 ques for fish weight you said trim the last part of b and now a=b let us take the 2nd sample where a[]={2,3,5,7} and b[]={2,3,3,5} and thus a[2]>b[2] i.e ai>bi so, ans should be Yes or i am reading it in wrong way i.e using only last n samples of b?
You need to sort it in decreasing order first. So A[] = {7,5,3,2} and b[] = {5,3,3,2} and thus as you said a[1] > b[1] and so the answer is Yes.
what is the output for div2-d if the input is :
2 2 500 1 2 500 1
if w1 = 1 and w2 = 500, then alice = 1 + 1000 = 1001, and bob = 500 + 500 = 1000, so, it should be "YES" right ?
I'm very bad at "find one solution",and the solution is very simple, like Div-C of this contest or #170 div1-B (http://www.codeforces.com/contest/277/problem/B) I can hardly invent them...
Is there any typical way of thinking? also, would someone give me some training problems like these?
I have another solution in div1-C which I prefer to share with you my solution : consider the array s sorted , now for ( 1<=i && i<=n/3 ) a[i]=0 , b[i]=s[i] ; for (n/3+1<=i && i<=2n/3) b[i]=0 , a[i]=s[i] and finally for (i>2n/3) a[i]=n-i+1 , b[i]=s[i]-(n-i+1) It can easily be shown that the sequence is almost unique.
I know that it is a bit later but after think a lot the problem 297D, I have the equation to solve: constraints satisfied >=0.75*(total constraints) . That is : n*(m-1)+ceil(m/2)>=0.75*(n*(m-1)+m*(n-1)) then you have m>=n That's all! (Sorry for my poor english)
My mind just got blown by D div1's solution. Soo simple but yet didn't come even close.
In 297A I'm not sure about the statement "Notice that we never remove digits from 'new part' of a."
Consider a="00001" and b="01001", we should augment a to be "00001101", and eventualy delete "000011" at the end, which means we will actually be remove characters from the "new part" of a. Am I wrong about this?