I came across this problem in which you have been given a directed graph $$$G=(V,E)$$$ with $$$|V|,|E|\leq 10^5$$$ and one additional edge can be added to $$$E$$$. What can be the maximum size of a strongly connected component in the resulting graph?
If anyone knows an approach, do share.
Thanks.
EDIT: I apologize that the $$$O(V.(V+E))$$$ algorithm that I thought would solve this also turned out to be incorrect.











deleted.
Consider such a case. The maximum sum path would suggest 1+5+3. But the actual answer here is 10 (by joining sink SCC of left diamond to its source SCC, we get 1+2+3+4 in one SCC)
The image isn't loading for me. Can you try again or give input in text form?
Yeah, my bad. Check now
First create a condensation graph, it will be a DAG(with multiple sources and sinks)
in condensation graph make sure to store number of nodes(original graph) for each node(SCC or dag's node)
for every sink calculate the number of nodes and from which source you achieved the max nodes( this can be done using simple graph dp)
connect the sink to the source(you stored), this should give the required graph. This can be achieved in O(V+E) as only dfs is used here couple of times
This is what I thought of. Unfortunately it has a worst case of $$$O(V(V+E))$$$ because you might need to traverse a significant portion of graph in every dfs call (due to overlapping) and the dfs will be called for as many sinks there can be (which can be $$$O(V)$$$)
You don't have to do dfs for every sink you can find max number of nodes in every sink in single dfs
first do a topological sort on condensation graph
go in order and perform dfs and when you return from a recursion store the maximum number of nodes from the child nodes( here you will visit every node every time)
something like this
EDIT : Here is a problem which uses the same idea
What you have achieved will be the maximum sum path of the condensed graph. Look at the case above (in the image). This algorithm will only find one path with maximum nodes sum. It would fail on the case with a diamond because it'll only output the sum achieved through heaviest path.
yep I was wrong, please update this blog if you get some better solution from different source
What is the problem source?
Codenation Innovation Labs Placement Test
Best I could think of was an O(V(V+E)) approach.Share it please.
Make a metagraph $$$G'$$$ where each node has a value equal to the size of SCC it represents. Let $$$ans= -inf$$$
For every source $$$s$$$ in $$$G'$$$ do,
As I understand from your comment, you fix source $$$s$$$, than run some $$$dfs$$$ to calculate $$$table[t]$$$ for all $$$t$$$, and than claim that after your calculations $$$table[t] = \sum_{v} value[v]\cdot f(s,v)\cdot f(v,t)$$$, where $$$f(u,v) = 1$$$ if $$$v$$$ is reachable from $$$u$$$, else $$$0$$$. I cant get how your first step calculates this sum, what do you mean by propagating something to children? Need some formal explanations.
Yes, I realised this algorithm wouldn't hold up. While propogating values to the descendants, we might run into duplicacies in case where the descendants later happen to lead to common nodes. Sorry but my $$$O(V.(V+E))$$$ algorithm is incorrect.
This looks unsolvable, because solving this is as hard as telling the number of reachable nodes for each node in a DAG, which is a known problem and only has approximations in sub-quadratic time. Correct me, if I'm wrong.
[Deleted]it wont work , I misread the ques.
Cant we find out the number of reachable nodes by iterating through the nodes in the reverse order of topological sorted order and say that dp[u]+=dp[v] for every (u,v) edge.Since this is a DAG I think this way the number of reachble nodes can be counted. Please correct me If I am wrong
This will over count whenever some path starting from two childs of u overlap. For example: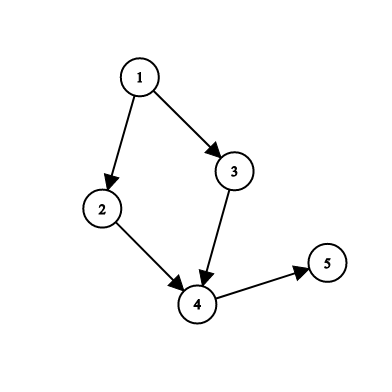
You'll have $$$dp(3) = 3$$$ and $$$dp(2) = 3$$$, but $$$dp(1)$$$ is not $$$3+3$$$.
Is it really from some hiring test? Writing "atmost" and "<=" seems so unprofessional. (Also the word order is very strange in "Find the maximum size...")
I like "find the maximize size" even more:)
Professional or not , but people will always judge you. So you only solve problems which are written professionally? Sorry not everyone is pro as you. They made mistakes that's why they are called as humans.
What exactly is the point of this comment? How are "being pro as me" or "people will always judge you" even related to all this? And I have not said I wouldn't solve problems like this, but I'd certainly form a certain opinion about this company or agency.
I would also like to point out that my original comment wasn't even really a criticism. I was just expressing my shock — I found it totally unbelievable that a professional could write like this. You are unreasonably defensive for some reason.
People make mistakes, it's more about being able to prevent mistakes. Hiring an editor or even just proofreading, for example.
Nowadays it feels like GrammerForces ,before asking for help you have to think a lot whether you should ask or not because some pro Coder will comment about their English or say how they should ask for help. Feels like I am in University where I have to think what others will say If ask this doubt. I comment something and it triggered you, then you suggest something for the solution. I understand it's the author's mistake. " I found totally unbelievable that a professional could write like this " . Awww Do I have to prepare a list of CF unrated rounds happened because of author's solution issues?
Sorry for my poor english. I just want to say keep it simple and sweet . Do codeforces not grammar or englishforces. Sorry for bothering you. GLHF
You can take 1 minute to fix your comment
Nowadays it feels like GrammarForces, before asking for help you have to think a lot whether you should ask or not because some pro Coder will comment about their English or say how they should ask for help. Feels like I am in University where I have to think what others will say if ask this doubt. I comment something and it triggered you, then you suggest something for the solution. I understand it's the author's mistake. "I found totally unbelievable that a professional could write like this". Awww Do I have to prepare a list of CF unrated rounds happened because of author's solution issues?
Sorry for my poor english. I just want to say keep it simple and sweet. Do codeforces not grammar or englishforces. Sorry for bothering you. GLHF
Btw the only real word I changed was GrammerForces to GrammarForces but as I can see in the last line you can write grammar properly if you try (and that typo could have been on purpose, idk). There are some other issues with the choice of past/present and maybe one letter wrong here and there but those aren't as important as proper punctuation and spacing.
Why did you even write this? The problem here is that author`s solution is some unproven shit, and as I understand nobody can propose solution for a given problem even in $$$\mathcal{o}(n^3)$$$. So yes, problemsetter is unprofessional.
Even though I don't care about the markup, which might be unavailable to technical difficulties, there is a huge problem in grammatical errors, cause they lead to misunderstanding and are as said "unprofessional". Just imagine seeing such a text in your workflow. Also the solution (even close to reality, which works with good probability) remains unknown, so I would love to see the official editorial, cause the author is either a genius or his solution is completely wrong.
Do you have a reduction? (I also think this problem is unsolvable, but I can't really show it either).
Also, did you mean to write "at least as hard as" or really "as hard as"? If it is as hard as counting reachable nodes, we could have a fast solution with "bit-parallelism".
Yeah, I definitely meant at least as hard. And unfortunately I know nothing about "bit-parallelism".
https://cses.fi/problemset/task/1685
Could you help me in this? I find out it similar to the above problem.
Just count the sources and sinks in SCC and then output the maximum of them.
Bitsets?
Oh, I've never heard of that name. Still I can only think of improving the naive solution, which wouldn't be even close.