Наименьший общий предок и подвешивание деревьев друг за друга (Online) && (O(log n)).
Постановка задачи:
Дается изначально лес подвешенных деревьев. Дальше следуют запросы двух видов:
Найти наименьшего общего предка двух вершин a и b, или вывести то, что они в разных деревьях.
Провести ребро между вершиной u и вершиной v. Гарантируется, что вершины u и v в разных деревьях, а также что, вершина u это корень дерева. (Получается после проведения ребра между вершиной u и v, они сольются в одно дерево, корнем которого будет корень дерева, в котором была вершина v)
Пример соединения двух деревьев, путем проведения ребра между двумя вершинами, выделенными красным
Решение:
Напомню, что задачу о нахождении LCA ( Lowest Common Ancestor ) сводится к задаче RMQ ( Range minimum query ), или по-русски, минимум на отрезке. Более подробно про это прочитать можно здесь и здесь.
Если бы задача была offline, мы смогли бы решить ее c помощью Sparse Table и DSU. Так как, задача бы просто свелась к нахождению LCA.
LCA двух вершин либо есть, так как они в одном графе, и никогда больше не изменится, как бы мы не "склеивали" деревья, либо его нет, так как они "еще" ни в одном дереве. Значит, нам просто нужно поддерживать для каждого запроса LCA в одном дереве вершины или нет, если в одном то ответ, это уже заранее посчитанное их LCA в конечном графе.
Асимптотика была бы O(1) на запрос (если использовать DSU со всеми эвристиками, то можно сказать константное время работы, Sparse Table отвечают на запрос за O(1)) и n log n предподсчет.
Итак, а как же решать если online.
Я предлагаю, вместо довольно хорошей структуры Sparse Table использовать Декартово дерево по неявному ключу. У него конечно ответ на запрос не O(1), да и не чистый log2. Однако с помощью него мы сможем вставлять одну последовательность в другую. Это нам нужно чтобы, поддерживать корректный эйлеров обход графа. Получается, если мы сможем за log:
поддерживать корректный эйлеров обход каждого дерева из нашего леса,
знать местоположение в этом обходе для каждой вершины,
за log находить минимум на отрезке,
то мы решили задачу.
Чтобы поддерживать корректный эйлеров обход заметим, что при соединении двух деревьев, эйлеров обход получившегося дерева не сильно изменится относительно их обоих. Назовем Д1 дерево к которому присоединяют, а Д2 дерево, которое присоединяют, v — вершина к которой присоединяют Д2.
Эйлеров обход Д1 выглядит как ... v, child v, child child v ... v, ... . Чтобы объединить Д1 и Д2 нам нужно всего лишь, после первого вхождения вершины v вставить эйлеров обход Д2, а также добавить еще раз вершину v.
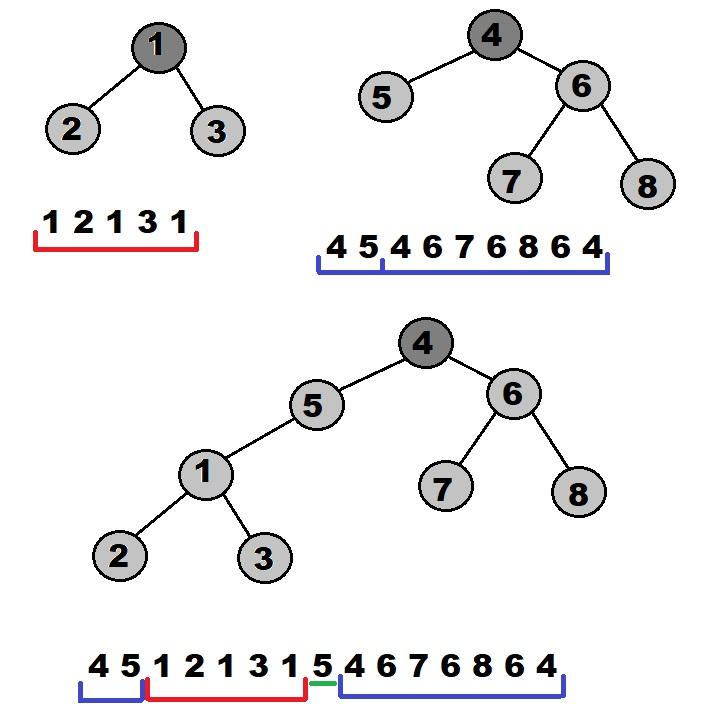
Итак, это мы научились просто поддерживать корректный эйлеров обход. Но нам надо еще ведь отвечать на минимум на отрезке, а значит нужно поддерживать глубину для каждого элемента в данном массиве. Заметим, что это просто прибавление на отрезке, так как вся глубина Эйлерова обхода сдвинется на одно и то же число в глубину, это deep(v) + 1. Массовые операции делаются не сложно с помощью метода проталкивания информации в детей.
Теперь самое сложное — запрос LCA, допустим с помощью системы непересекающихся множеств, мы поняли что вершины в одном дереве. (Декартового Дерево — далее ДД, дерево, с которым мы работаем задаче — далее дерево(обыч))
Как минимум, у нас два вопроса:
А кто корень ДД в нашем обходе по этому дереву(обыч)?
А где находится первое вхождение вершин этих в нашем ДД?
Чтобы отвечать на эти вопросы, поймем, что первое вхождение вершины это то, просто когда мы вошли в нее из родителя, а не продублировали обходя ее детей. То есть если изначально у нас было две дерева, каждое которое из одной вершины, их обходы это: 1 и 2, при соединении их 1 2 1 появится копия первой вершины, которая на самом деле, очевидно, идет позже, чем та вершина, которая была изначально. Это значит, что появившиеся впоследствии копии вершин нас не интересуют, мы всегда знаем (!) в памяти (!) где лежит вершина, которая первое вхождение, — это та, которую мы создали в самом начале. Итак, если мы знаем, где лежит в памяти вершина, которая первое вхождение, то мы можем вычислить ее номер в ДД, поднимаясь от нее по ДД до корня ДД. Для этого, у каждой вершины будем хранить ее родителя и тип связи (мы левый сын или правый).
Тогда подъем будет выглядеть так:
int pos(vertex* v) {
if (v == NULL) return 0;
int ans = pos(v->parent);
if (v->type == 0) ans -= cnt(v->r) + 1;
else ans += cnt(v->l) + 1;
return ans;
}
type == 0 значит мы левый ребенок, в ином случае мы правый. cnt(v) — количество вершин в поддереве вершины v. Выяснить, почему это правда, — задачка для читателя))
Аналогично, будем находить корень ДД для вершины:
vertex* lead(vertex* v) {
if (v->parent == NULL) return v;
return lead(v->parent);
}
Хорошо, осталось написать весь оставшийся код, да еще и без ошибок). Объявим саму вершину ДД:
struct vertex {
int num, deep, add, cnt, prior;
pair<int, int> min;
vertex* r, * l, * parent;
int type;
};
num — Это номер вершины в дереве(обыч), deep — ее глубина, соответственно. add — это прибавка к глубине, она нужна для массового прибавления, cnt — количество вершин в поддереве, prior — рандомное число, чисто механика ДД, также нужно поддержка значения минимума и номера минимума, заведем для этого пару (ифать меньше в итоге). Сделаем переход к детям и родителю, а также, как уже выше писалось, тип связи с родителем.
Сделаем две функции, на получения cnt и минимума в вершине:
int cnt(vertex* v) { if (v == NULL) return 0; return v->cnt; }
pair<int, int> min2(vertex* v) { if (v == NULL) return { INF, -1 }; return v->min; }
Обновление \ пересчет вершины и проталкивание информации в детей.
#define st first
#define nd second
void upd(vertex * v) { // Обновление cnt, min + родителей
if (v == NULL) return;
if (v->l != NULL) v->l->parent = v, v->l->type = 0; // Если вый ребенок то type 0
if (v->r != NULL) v->r->parent = v, v->r->type = 1; // Если правый то 1
v->min = min(min(min2(v->l), min2(v->r)), { v->deep, v->num }); // Мин. в v это мин. между ее детей и ее самой
v->cnt = 1 + cnt(v->r) + cnt(v->l); // Кол-во вершин в поддереве v это кол-во
} // вершин в ее детях плюс она сама.
void push(vertex * v) {
if (v == NULL) return;
v->deep += v->add; // при пуше вершины, будем считать что значение в ней всегда верно,
v->min.st += v->add; // входя в нее всегда будем пушить, а обновлять только когда пропушены дети
if (v->l != NULL) v->l->add += v->add;
if (v->r != NULL) v->r->add += v->add;
v->add = 0;
}
Обычный Split и merge, с учетом проталкивания информации:
#define st first
#define nd second
vertex* merge(vertex * l, vertex * r) {
push(l);
push(r);
if (l == NULL or r == NULL) {
if (l == NULL) return r;
else return l;
}
if (l->prior > r->prior) {
l->r = merge(l->r, r);
push(l->l);
upd(l);
return l;
}
else {
r->l = merge(l, r->l);
push(r->r);
upd(r);
return r;
}
}
pair<vertex*, vertex*> split(vertex * T, int key, int add = 0) {
if (T == NULL) {
return { NULL, NULL };
}
push(T);
int z = add + cnt(T->l);
if (z < key) {
auto t = split(T->r, key, z + 1);
T->r = t.st;
push(T->l);
upd(T);
return { T, t.nd };
}
else {
auto t = split(T->l, key, add);
T->l = t.nd;
push(T->r);
upd(T);
return { t.st, T };
}
}
Создадим сразу все нужные нам вершины, их всего N, а также напишем СНМ:
const int N = 1e5 + 2, INF = 1e9;
vector<vertex*> ver(N); // Вектор вершинок, не забудем в main'e инициализировать
int boss[N], rang[N]; // Не забудем в main'e инициализировать массивы (в них не должны лежать 0)
int get_boss(int a) {
if (boss[a] == a) return a;
boss[a] = get_boss(boss[a]);
return boss[a];
}
void dsu(int a, int b) {
int x = get_boss(a);
int y = get_boss(b);
if (rang[x] > rang[y]) swap(x, y);
boss[x] = y;
rang[y] += rang[x];
}
Объединение двух деревьев будет выглядеть так:
#define st first
#define nd second
void unite(int a, int b) {
auto T = lead(ver[a]); // Получим корень ДД для вершин, чтобы работать уже с их деревьями (Это важно, так как
auto T2 = lead(ver[b]); // корень дерева(обыч) != корень ДД
int ps = pos(ver[a]); // Найдем позицию вершины а в дереве, чтобы знать куда вставлять другое ДД
auto t = split(T, ps);
auto d = split(t.st, ps - 1);
T2->add += d.nd->deep + 1; // ДД d.nd - это дерево из одной вершины, к которой мы приставляем другое ДД
vertex* v = new vertex{ ver[a]->num, d.nd->deep, 0, 1, rand(), {d.nd->deep, ver[a]->num}, NULL, NULL, NULL, 1 }; // Создаем копию нашей вершины, до этого выше мы извлекли ее в дерево d.nd, чтобы получить корректную глубину
T = merge(merge(d.st, d.nd), T2); // Соединяем все в правильном порядке
T = merge(T, v);
T = merge(T, t.nd);
dsu(a, b); // Объединяем вершины в СНМ
}
Получение наименьшего общего предка:
int lca(int a, int b) {
if (get_boss(a) != get_boss(b)) return 0; // Проверка в одном дереве они, или нет
auto T = lead(ver[a]); // Получим корень ДД, в котором они лежат
int p1 = pos(ver[a]); // Найдем их позиции там
int p2 = pos(ver[b]);
if (p1 > p2) swap(p1, p2);
auto t = split(T, p2);
auto d = split(t.st, p1 - 1);
int ans = d.nd->min.nd;
T = merge(merge(d.st, d.nd), t.nd);
return ans;
}
Main:
int main() {
for (int i = 0; i < N; i++) rang[i] = 1, boss[i] = i;
for (int i = 0; i < N; i++) {
ver[i] = new vertex{ i, 0, 0, 1, rand(), {0, i}, NULL, NULL, NULL, 1 };
}
Это все, что нужно для решения задачи. (Если граф задается сначала уже какой-то, то мы просто создаем его используя unite())
Вывод:
Где можно посмотреть и сдать задачу.
Мой код к ней.
Асимптотика:
Создание леса:
n log nОбъединение:
log n, однако там довольно не маленькая константа, так как, у ДД в целом, она не маленькая и операции в нем не быстрые, так у нас их в еще и много, а еще мы несколько раз поднимаемся по нему. Но в любом случае это log =)Нахождение LCA:
log nаналогично, и аналогично большая константа.
Когда я столкнулась с этой задачей, подумав времени x, я решила погуглить. К сожалению, не найдя ничего хорошего в русскоязычных ресурсах, пришлось смотреть в англоязычных. И там, либо плохо искав, либо я хз, тоже ничего внятного нет. Придумав решение, захотелось поделиться им, чтоб потомкам было легче).
P.S. На codeforces уже был пост с этой темой пятилетней давности, в котором, два человека рассказали максимально не понятные решения, одно из которых, судя по всему, даже не работает, либо будет слишком долго работать, так как его асимптотика не log на запрос, а n log n.
Если вы знаете, как еще можно решать эту задачу, я была бы рада, если бы вы поделились. Также, если вы найдете багу в коде, было бы тоже неплохо, но вроде их нет)).











Вообще-то можно просто линкат написать....
Что это и от чего сокращение? А link-cut , поняла. Ну хз, что проще из этого))
После этих слов автор потратил часов 20 своей жизни
СПАСИБО!!!! КАК РАЗ ИСКАЛ!!!!! всё просто и понятно, оформление — ОГОНЬ!!!!!
Насколько я понял из комментария, skrydg предлагает решать задачу двоичными подъёмами. Этот вариант наверно работает быстрее, чем ДД, да и кода вроде бы будет поменьше, только надо разобраться в методе.
Не уверен, что я правильно понял автора комментария, потому что у него асимптотика log^2 на запрос. Кое-что я додумал сам, после чего получил log (амортизированный) на запрос, что наверняка не хуже. Идея такова:
1) Храним двоичные подъёмы для каждой вершины на всевозможные степени двойки. Если вершина недостаточно глубока (поднявшись на 2^k, мы вершину не найдём), запишем -1.
2) Ещё храним двоичные спуски. Это тоже двумерная матрица, как и двоичные подъёмы, но не вершин, а списков вершин. В ячейке $$$down[2^k][x]$$$ лежат все такие вершины y, что $$$up[2^k][y] == x$$$. Этой идеи я не увидел, но, кажется, без неё ломается асимптотика.
Мы предполагаем, что в любой момент (между запросами) времени подъёмы и спуски посчитаны корректно.
3) Если нам поступил запрос LCA, то отвечаем на него, как в стандартном алгоритме поиска LCA, двоичными подъёмами. Единственное отличие — для алгоритма надо сначала поднять вершины из запроса на один уровень, а мы не знаем их глубину. Но мы можем её узнать за log, пытаясь подняться из вершины как можно выше.
4) Теперь нам поступил запрос подвешивания. Это самое интересное. u — корень дерева, v — другая вершина, подвешиваем u за v. После этого подвешивания матрицы двоичных подъёмов и спусков изменятся. Как? Только добавятся некоторые двоичные подъёмы из дерева с u и некоторые двоичные спуски из дерева с v. Для обновления можем написать рекурсивную процедуру типа
и вызвать её как
update(u, v, 0). Как ни странно, суммарно запросы подвешивания будут стоить дёшево — обещанный амортизированный log. Функцияupdate, хотя и рекурсивная, вызывается не очень часто — во-первых, после каждого запроса подвешивания, которых не больше q, а во-вторых, после каждого добавления информации в матрицы up или down. Но в них суммарно лежит не больше O(nlogn) вершин. Собственно говоря, всё.UPD: Хотел сделать мелкий bug fix, но CF заглючил и теперь у этого комментария куча версий...
Правда надо обращаться не
up[1 << k][u], аup[k][u], но это уже детали реализации. Можно считать, что у меня это hashmap)Хм, звучит как хорошая идея. Попробую разобраться, спасибо!)
Еще можно сделать такой ход конем: давай просто хранить бин подъемы (можно без костылей с глубокими вершинами).
Теперь напишем наивный алгос LCA. Если одна вершина не может прыгнуть выше, то просто поднимаемся до челика, к которому подвесились. И так делаем бин подъемы. Понятно, что если было k подвешиваний, то все это работает за O(klog), и кажется, несложно реализовать за (k + log), ну а перестроить все можем за nlog. Так что просто делаем корнячку, и это пишется супер легко, и нет никаких костылей, и работает, скорее всего, быстрее ДД (Особенно учитывая, сколько в нем updatов различных)
Эм, а зачем? Во-первых, неясно, как отвечать на запросы за O(k + log). Даже если и можно, то корнячка сломает асимптотику на что-то типа O((n + q)√(nlog + qlog)). Это может и быстрее ДД, хотя не факт, но уж медленнее метода с подъёмами-спусками. Ну, и кода в предложенном мною методе тоже немного.
Ну да, просто как фан факт, да и если ты забыл идею, то это не так уж и больно вспоминать
Кстати, похоже, можно и без двоичных спусков. Тогда, как сказано в вышеупомянутом комментарии, если
up[k][v] == -1, то рекурсивным спуском можно проверить, правда ли там -1. И будет именно то, что и написано, то есть log ^ 2.В качестве кода всё просто, даже проще, чем если добавить двоичные спуски. Напишем функцию
Пусть мы в произвольном месте программы вызвали
get(k, v). Тогда можно увидеть, что если она вернёт не -1, то столько же раз рекурсивно вызовется, сколько и запишет дополнительную информацию вup. То есть суммарная стоимость таких вызовов $$$O(nlog(n))$$$ и про это можно забыть. Если же вызов вернёт -1, то это потребует $$$O(k) = O(logn)$$$ времени дополнительно.Запрос подвешивания делаем, записав
up[0][u] = vЗапрос получения LCA делаем так. Вычисляем глубину вершины, пытаясь подняться из неё на $$$log(n), ...,2, 1$$$. Если нам не повезло, то все разы мы не могли подняться и потратили $$$O(log^2(n))$$$ времени. После этого используем стандартный алгоритм с двоичными подъёмами, который тоже займёт не более $$$O(log^2(n))$$$.
P. S. Кажется, асимптотику можно улучшить до логарифма. Самый простой способ, который я вижу — если
up[k][v] == -1, то рядом хранить время (целое число $$$t \in [0; q]$$$), показывающее, когда эта -1 актуальна. Тогда (кажется), добавивifв рекурсию, асимптотика упадёт до $$$O(nlog(n) + qlog(n))$$$. Ну, тут кому что писать приятнее, я бы выбрал двоичные спуски)Мне вот стало интересно, умеет ли Euler Tour Tree (это так называется структурочка, что ты описала) поддерживать переподвешивание за другую вершину, мне кажется, что это похоже на правду, но за минуту на листочке я не придумал
Переподвешивание за другую вершину можно делать за O(1). Просто тогда для каждого дерева будем помнить его настоящего и активного корня, пришел запрос на смену корня, перезапишем активного. Все больше ничего не будем делать.
Ответ на запрос lca будет
lca(u, v) ^ lca(u, root) ^ lca(v, root), u v — запрос, root — активный корень. Почему это работает задачка для читателя)))Да, ETT умеет переподвешивать дерево, для этого нужно из конца удалить одно вхождение корня (чтобы после не было подряд идущих дубликатов), циклически сдвинуть обход так, чтобы он начинался со старого поддерева нового корня, и в конец дописать еще одно вхождение корня.
Что только что проихошло: мы сохранили старое поддерево нового корня, обошли его в самом начале, а после дошли от нового корня до старого, обойдя половину дерева, и обратно, обойдя вторую половину дерева (за вычетом поддерева нового корня) и сказали, что все, что мы только что обошли это еще одно поддерево нового корня (на словах выглядит ужасно, вот не менее ужасный пример): Изначальный ETT:
1 2 1 4 5 4 6 4 1 7 1Вот то, что произойдет при переподвешивании за вершину 4:
4 5 4 6 4 1 7 1 2 1 4Старое поддерево вершины 4 (
4 5 4 6 4) перенесли в начало, все, что было до нее (1 2 1) циклически улетело в конец, и туда же мы дописали еще одно вхождение нового корня (4)PS. К сожалению, лень не позволяет мне нарисовать иллюстрации к алгоритму и примеру, так что придется положиться на собственное воображение
Прекрасная статья, спасибо. Сильным упрощением кода является избавление от DSU — оно здесь не нужно. Достаточно сделать следующее при запросе: