Problem A
The solution of the problem based on modeling of the decribed process. It is important to perform a pass throw the beginning correctly. You can take the current number modulo n (and add 1), or you can subtract n every time the current number increases n.
Problem C
First of all, count the number of hamsters in the sequence. Let it is h. Try positions where the sequence of hamsters will start, and for each position count the number of tigers in the segment of length h starting from the fixed position. These tigers should be swapped with hamsters in a number of swaps equal to the number of tigers not in proper places. Choose minimum among all starting posotions.
Problem F
First, note that all the described operations are invertible: opening/closing doors, moving from one room to another and exchanging keys. So we may perform such operations from the initial arrangement to get some arrangment A, and then perform some operations from the final arrangement to get the same arrangement A, in this case the answer is "YES". Let apply the following strategy to both arrangements: while there is a person who can go to some room and open some door, perform this action. As a result from each arrangement we obtain subsets of connected rooms (we call them connected parts of the house), corresponding subsets of people and corresponding subset of keys in each connected part of the house. If these resulting subsets coincide for the initial and the final arrangement, then the answer is "YES", otherwise the answer is "NO". Indeed, if they coincide, it is obvious that we can get from the initial arrangement to the resulting arrangement, and then - to the final arrangement. Otherwise it is impossible, because there exist some keys that cannot be applied to the corresponding doors, because they are in another connected part of the house, or there exist people, who have no way to get to rooms in another connected part of the house.
Second, a few words about implementation. One of possible ways is to have two boolean matrices:
1) saying for each person if he/she could get to each room and
2) saying for each key the same,
and then recursively implement operations:
1) if a person can get to a room, try to get to neirbouring rooms,
2) the same for keys, but also trying to open a door to the neirbouring room,
3) if the door opens, people and keys in the incident rooms are assigned to another room.
So we try each pair person-room, person-door, key-door, key-room for O(1) times, and the total asymptotics is O(nk + km + m2 + nm).
Problem G
Note that the lengths of the sides can be 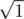 ,
, 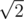 ,
, 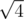 ,
, 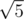 , and so on, i.e. the roots of integers, that can be represented as a2 + b2. Generate a proper quantity of such numbers. Denote them
, and so on, i.e. the roots of integers, that can be represented as a2 + b2. Generate a proper quantity of such numbers. Denote them 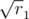 ,
, 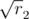 , ... In some cases we can take first n such numbers as lengths of sides, but in some cases we surely cannot. It depends on the parity. If the sum r1 + r2 + ... + rn is odd, it is impossible. Indeed, we can
, ... In some cases we can take first n such numbers as lengths of sides, but in some cases we surely cannot. It depends on the parity. If the sum r1 + r2 + ... + rn is odd, it is impossible. Indeed, we can
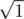 ,
, 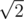 ,
, 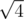 ,
, 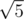 , and so on, i.e. the roots of integers, that can be represented as a2 + b2. Generate a proper quantity of such numbers. Denote them
, and so on, i.e. the roots of integers, that can be represented as a2 + b2. Generate a proper quantity of such numbers. Denote them 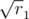 ,
, 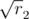 , ... In some cases we can take first n such numbers as lengths of sides, but in some cases we surely cannot. It depends on the parity. If the sum r1 + r2 + ... + rn is odd, it is impossible. Indeed, we can
, ... In some cases we can take first n such numbers as lengths of sides, but in some cases we surely cannot. It depends on the parity. If the sum r1 + r2 + ... + rn is odd, it is impossible. Indeed, we canrepresent each side by vector (xi, yi), xi2 + yi2 = ri (xi and yi may be negative). If ri is even, then xi + yi is even too. If ri is odd, then xi + yi is odd. If we form a polygon with vectors of the sides (xi, yi), then x1 + x2 + ... + xn = 0 and y1 + y2 + ... + yn = 0, so the total sum x1 + ... + xn + y1 + ... + yn must be even! But if r1 + ... + rn is odd, it is odd too, so to build a polygon is impossible.
Let us take r1, ..., rn if their sum is even, and otherwise take r1, ..., rn + 1 and throw away one of them to make the sum even (in my solution I throw away the greatest such number). For each ri choose non-negative xi and yi, xi2 + yi2 = ri. In general case there are 8 possible orientations of a vector: (xi, yi), ( - xi, yi), (xi, - yi), ( - xi, - yi), (yi, xi), ( - yi, xi), (yi, - xi), ( - yi, - xi). The current subtask is to find such orientation for each vector that their sum is zero. It can be done by the greedy algorithm. Let's take the vectors from the longest ones. We will calculate current vector sum that is initially (0, 0), and it will be updated by each new taken vector. At each step choose such orientation that the current vector with that orientation minimizes the current sum (by its length) being added to it. Then, when the vectors are oriented, sort them by polar angle and apply them consequently to get a convex polygon. The described algorithm finds a required polygon for all possible tests.









 +5
+5



