361A - Levko and Table
Matrix,in which all diagonal elements equal k and other elements equal 0, satisfied all conditions.
For example, if n = 4 and k = 7, our matrix will be
7 0 0 0
0 7 0 0
0 0 7 0
0 0 0 7
361B - Levko and Permutation
gcd(1, m) = 1, so if n = k, there is no suitable permutation.
It is well known that gcd(m, m - 1) = 1. Lets construct following permutation. It has exactly k good elements.
n - k 1 2 3 ... n - k - 1 n - k + 1 n - k + 2 ... n
360A - Levko and Array Recovery
Let's find such value b[i] that a[i] ≤ b[i] for all indeces i. Let's simulate all operations and diff[i] will be the difference between current value of i-th element and its initial value. If we have operation of first type, we change values of diff[i]. If we have operation of second type, we know that a[i] + diff[i] ≤ m[i], so a[i] ≤ m[i] - diff[i]. We will get array b when we union all this inequalities.
Let's prove that either b satisfied all conditions or there is no such array. It can be two cases, why b does not suit:
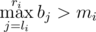 — it's impossible due to construction of array b.
— it's impossible due to construction of array b.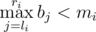 — b[i] is a maximal possible value of a[i], so
— b[i] is a maximal possible value of a[i], so 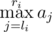 can't be bigger.
can't be bigger.
360B - Levko and Array
Let's solve this problem using binary search. We need to check whether we can achieve an array, when c(a) will be at most x. Lets make dp. dp[i] means minimal number of elements with indeces less than i, which we need to change, but we don't change i-th element. Let's iterate next element j, which we don't change. Then we know that we can change all elements between i and j. It is equivalent to such condition
|aj - ai| ≤ (j - i)·x
Difference between neighboring elements can be at most x. The maximal possible difference increases by x exactly j - i times between elements i and j, so this inequality is correct.
360C - Levko and Strings
Let's count amount of such substrings of t that are bigger than corresponding substring of s and begin at the position i.
If t[i] < s[i], this amount equals 0.
If t[i] > s[i], this amount equals n - i.
If t[i] = s[i], then let's find such nearest position j, j > i , that t[j] ≠ s[j]. If t[j] > s[j], needed amount of substrings will be n - j. If t[j] < s[j], needed amount of substrings will be 0.
We can rephrase this: If t[i] > s[i], it will be (1 + pref)·(n - i) new substrings, where pref means how many last elements in s and t is equal.
Let's make dp. dp[i][sum] means that we viewed i positions, have sum needed substrings and s[i] ≠ t[i]. Lets iterate their common prefix pref.
If t[i] < s[i], dp[i][sum] + = dp[i - pref - 1][sum]·(s[i] - 'a') — we can count this value using partial sums.
If t[i] > s[i], dp[i][sum] + = dp[i - pref - 1][sum - (1 + pref)·(n - i)]·('z' - s[i]). Let's iterate pref.
Let's note that sum - pref·(n - i) ≥ 0, so pref ≤ sum / (n - i) and pref ≤ k / (n - i). This means that third cycle will make at most k / (n - i) iterations when we find value of dp[i][sum]. Let's count total number of iterations:
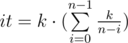 =
= 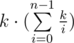 < k·(n + k·log k).
< k·(n + k·log k).
360D - Levko and Sets
p is prime, so there exist primitive root g modulo p(We don't need to find it, but we know that it exists). We can write ai = gri. Note, that i-th set consists of all numbers 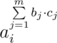 , where cj ≥ 0, or we can write it as
, where cj ≥ 0, or we can write it as 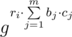 .
.
By Fermat's little theorem ap - 1 = 1 mod p we have that ak mod p = ak mod (p - 1) mod p. So 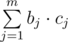 can be equal to all values k·t modulo p - 1, where t = gcd(b1, b2, ... , bm, p - 1). Note that t doesn't depend on ri, so we can assign g = gt. Then all elements of i-th set will be gri·k, where k ≥ 0. Now we can replace bi by qi, where qi = gcd(ri, p - 1), as we do with bi at the beginning. Then all elements of i-th set will be gqi·k, where k ≥ 0. This means that if we write all values g0, g1, ..., gp - 2 in a line, i-th set will contain every qi-th element.
can be equal to all values k·t modulo p - 1, where t = gcd(b1, b2, ... , bm, p - 1). Note that t doesn't depend on ri, so we can assign g = gt. Then all elements of i-th set will be gri·k, where k ≥ 0. Now we can replace bi by qi, where qi = gcd(ri, p - 1), as we do with bi at the beginning. Then all elements of i-th set will be gqi·k, where k ≥ 0. This means that if we write all values g0, g1, ..., gp - 2 in a line, i-th set will contain every qi-th element.
Now we need to find union of this sets.Let's do it using inclusion-exclusion principle. All our numbers are divisors of p - 1. Let's dpi be the coefficient near i in inclusion-exclusion principle(i is a divisor of p - 1) and we can find this values, adding all qi alternatively.
Also we need to find qi. Let's find volume of the i-th set. It is equal to 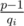 . From the other side it is equal to such minimal number di, that aidi = 1 mod p (di is a cycle). From aip - 1 = 1 mod p we have that p - 1 is divisible by di. So we can find di as a divisor of p - 1. And
. From the other side it is equal to such minimal number di, that aidi = 1 mod p (di is a cycle). From aip - 1 = 1 mod p we have that p - 1 is divisible by di. So we can find di as a divisor of p - 1. And 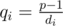 .
.
360E - Levko and Game
Algorithm:
Firstly we will solve problem if first player can win.
Let's make all roads that we can change equal to r[i] and do two Dijkstra's algorithms from vertices s1 and s2. Let's d1[i] be the distance from s1 to i, d2[i] be the distance from s2 to i. Consider a road, that we can change, from a to b. If d1[a] < d2[a], we will set length of such road equal to l[i] and do two Dijkstra's algorithms again. We run such process until any road changes its length.
If d1[f] < d2[f] after all changes then first player wins.
If we replace condition d1[a] < d2[a] by d1[a] ≤ d2[a], we can check if Levko can end this game with a draw.
Proof:
Let's call "edges" only roads which Levko can change. When we do Dijkstra's algorithm we use all roads, not only edges.
Let's prove that if there exist such edges values that first player wins, there exist values of edges such that first player wins and all this values equal either l[i] or r[i]. Consider shortest pathes of both players.
If only first player goes on edge from a to b, we can set its value l[i]. Proof: there must hold d1[a] < d2[a] because first player goes on it and wins. This condition holds after change of value of this edge. If second player goes on this edge, he loses because d1[f] ≤ d1[a] + d(a, b) + d(b, f) < d2[a] + d(a, b) + d(b, F) = d2[f]. If second player doesn't go on this edge, he loses because shortest path of first player became smaller(d(x, y) — shortest path from x to y).
If only second player goes on edge from a to b, we can set its value r[i]. Proof: Shortest path of the first player doesn't change and shortest path of second player can only become larger.
If no player go on edge, we can set its value r[i]. Proof: Shortest pathes of both players doesn't change.
If both players go on edge from a to b, we can set its value l[i]. Proof: Shortest pathes of both players decrease by (initial value of this edge — l[i]).
After every such operation first player wins again and all edges become either l[i] or r[i].Consider result of our algorithm. Let's call edge "good" if its value is equal to l[i] and "bad" if its value equals r[i].
(a) Let's prove that after performing all operations we will have d1[a] < d2[a] for all good edges (a, b). If we have d1[a1] < d2[a1] for edge (a1, b1) and after changing value of (a2, b2) this condition doesn't hold. We have d1[a1] > = d2[a1], d1[a2] < d2[a2]. We change only one edge and shortest path from s2 to f become shorter so edge (a2, b2) lies on this path.
d2[a1] = d2[a2] + d(a2, b2) + d(b2, a1) > d1[a2] + d(a2, b2) + d(b2, a1) ≥ d1[a1]. Contradiction. (b) Let's prove that after performing all operations we will have d1[a] ≥ d2[a] for all bad edges. We can continue our procces otherwise.
(c) Let's prove that if condition d1[a] < d2[a] holds for some edge but we doesn't change it on this iteration, this continion holds after this iteration. Proof is same as in (a).
(d) Let's prove that if any subset of good edges is equal to l[i] and d1[a] < d2[a], ift also holds when we make all good edges equal l[i]. Let's simulate all procces and use (c).Lets prove that for all edges values(not necessary only l[i] or r[i]), d1[a] ≥ d2[a] for all bad edges (a, b).
Assume that we have such edge. Consider shortest path of first player to its beginning. If there exist bad edges (a1, b1) on this path, there must holds inequality d1[a1] < d2[a1]. Consider first of this bad edges (a, b). Then shortest path of first player to a doesn't consist any bad edge. Consider problem,m which is equivalent to our problem but finish is in vertex a. good and bad edges will be same. Let's change all value of edges as we do in item 1. Note? that all bad edges will be equal to r[i]. So only subset of good edges can be equal to l[i] and d1[a1] < d2[a1]. By (d) we have that we can set all good edges l[i] and condition d1[a1] < d2[a1] will be satisfied. So we have contradiction thst this edge is bad.This means that if first player goes on any bad edge, he loses. So we can set r[i] to all this edges. So we can set l[i] to some subset of good edges. By (d) we have that if we have d1[f] < d2[f] for some subset of good edges, this condition will be true if we set all good edges l[i].
Note that proof will be same if we want to check whether Levko can end a game with a draw.











Is the English version available ?
Yes, you can read it here: http://codeforces.com/blog/entry/9529?locale=en
B can be done in O(n log^2 n). Firstly we draw n points on plane — namely (i, a[i]). We binary search on result. We can achieve value l (given by binary search) if there exists a broken line passing through at most n — k points with absolute value of slope not exceeding l. In order to check that we flatten whole coordinate system l times (with respect to OY axis), that is replace (i, a[i]) with (i, a[i]/l). Now, we want to check if there is a broken line passing through n — k points with absolute value of slope not exceeding 1. In order to check that we rotate whole coordinate system by 45 degrees and use interval tree :).
So sad that I couldn't come up with easier solution and chose not to implement that solution I described :P.
great !
Can you explain second part, why it is helpful to rotate coordinate system by 45 degrees? Slope also can be a floating number, How we will use interval tree?
After rotating by 45 degrees (counterclockwise) lines with slope 1 are vertical ones and lines with slopes -1 are horizontal, so our problem reduces to the following one: n points on the plane are given. We have to find largest p such that there are p points (x1, y1), ..., (x_p, y_p) among these n points such that x_i <= x_(i+1) and y_i <= y_(i+1). This is a well-known example of using interval tree. I hope that this is clear enough, After marking these points (i, a[i]) our problem is a special case of problem http://codeforces.com/contest/249/problem/D (but is solvable with exactly the same algorithm).
Note that we can avoid using floating numbers. What we want to know is only an order of points due to coefficients b_i, where y_i = l*x_i + b_i and due to coefficients c_i where y_i = (-l) * x_i + c_i which can be easily determined by comparing points with cross product.
Very great solution ! thank you very much!!! Everything is clear now.
I think x[i] <= x[i + 1], y[i] <= y[i + 1] can be also solved using Set. :)
Where is the solution for D & E ?
I still could not get the idea behind 360A, can someone explain in simpler words? Thanks in advance.
Each answer to the query (T=2)will give numbers in [l,r] a upper bound.(The numbers can't exceed the maximum.) For the first time of iteration, find the maximum possible value of each number, then iterate again and if all querys have correct answers(there is at least one element equals the answer),then the answer is yes. Otherwise, the answer will be no.
Can anyone explain the solution of 360A — Levko and Array Recovery ?????
Can anyone explain more clearly the DP in 360B - Левко и массив
For problem Div1 D, can r[i] be computed more efficiently than iterating through all the divisors d of P-1 and finding the smallest one such that a[i]^d = 1 (mod P)?
Yes. Begin with d = p — 1 and divide d by two until d is divisible by 2 and a[i]^(d/2) = 1 mod P. Do the same with 3, 5 and so on.
For problem Div1 D,at this test,many accepted solution will be hacked:
2 1 13
3 5
1
The correct answer is 6,but many accepted solution output 7.
I agree with you, as for this test 2 1 37 31 27 1 The correct answer is 8, zhj ans sspa's solutions output 10, but sevenkplus's solution output 8. Are the tests too weak?
E can be solved in O((V+E) log (V+E)) time :). For details see my code: http://codeforces.com/contest/360/submission/5607748 .
Funny that it was the easiest problem for me from this contest. A, B, D took me I think at least 10 minutes to come up with an idea of solution and this one was straightforward for me :P.
Can anyone explain div1 B clearly. I am unable to understand the editorial.
test cases are weak for example this accepted solution should not pass https://codeforces.com/contest/360/submission/99302293 as the correct answer for this test case 4 2 2 1 2 3 1 4 1 2 4 1 1 3 3 3 4 3 1 3 would be WIN 3 3 but the accepted solution mentioned above would give DRAW 3 1 as the answer