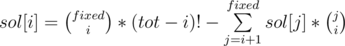430A - Points and Segments (easy)
The problem asks you to output “-1” if there is no solution. A natural question is now: “when there is no solution”? Try to come up with a test like this!
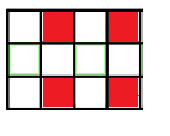
After some analysis, you’ll see anyhow we draw the points and the lines, there will always be a solution. By manually solving small cases, you might already have found the pattern. But for now, let’s assume anyhow we draw points and lines, there will always be a solution. Let’s have a fixed set of points. Then, anyhow we draw a line, there should still be a solution. So, we need to find a coloring of points, such as for every line, |number of red points which belong to it – number of blue points which belong to it| <= 1.
Suppose anytime you color a point with red you assign it +1 value. Also, anytime you color it with blue you assign it -1 value. Then, for a segment, the drawing is good if S = sum of values assigned to points that belong to segment is between -1 and 1 (in other words |S| <= 1). Let’s sort points increasing by abscissa. It’s useful because now, for a segment, there will be a contiguous range of points that belong to that segment. For example, suppose my current segment is [3, 7] and the initial set of points was {4, 1, 5, 2, 8, 7}. Initially, points that belong to the segment would be first, third and sixth. Let’s sort the points by abscissa. It looks like {1, 2, 4, 5, 7, 8}. You can see now there is a contiguous range of points that belongs to [3, 7] segment: more exactly third, fourth and fifth.
We reduced problem to: given an array, assign it either +1 or -1 values such as, for each subarray (contiguous range), the sum S of subarray’s elements follows the condition |S| <= 1. Before reading on, try to come up with an example by yourself.
My solution uses the pattern: +1 -1 +1 -1 +1 -1 ... Each subarray of it will have sum of its elements either -1, 0 or 1. How to proof it? When dealing with sums of subarrays, a good idea is to use partial sums. Denote sum[i] = x[1] + x[2] + ... + x[i]. Then, sum of a subarray [x, y] is sum[y] – sum[x – 1]. Partial sums for the pattern looks like: 1 0 1 0 1 0 .... Hence, there are 4 possible cases:
1/ sum[x – 1] = 0 and sum[y] = 0. sum[y] – sum[x – 1] = 0
2/ sum[x – 1] = 1 and sum[y] = 1. sum[y] – sum[x – 1] = 0
3/ sum[x – 1] = 0 and sum[y] = 1. sum[y] – sum[x – 1] = 1
4/ sum[x – 1] = 1 and sum[y] = 0. sum[y] – sum[x – 1] = -1
Hence, each subarray sum is either -1, 0 or 1. So, general algorithm looks like: sort points by abscissa, assign them red, blue, red, blue, ... and then sort them back by original order and print the colors.
430B - Balls Game
This is an implementation problem. There is not so much to explain. Perhaps the trick at implementation problems is to divide code into smaller subproblems, easy to code and then put them together. I don’t know if this is the universally truth, but this is how I approach them. Here, there are two main parts: the part when you insert a ball between 2 balls and the part when you see how many balls are destroyed after the move. We can keep an array a[] with initial configuration of balls, then for each insertion create an array b[] with current configuration after the insertion. If my ball is inserted after position pos, b is something like this: b = a[1....pos] + {my_ball} + a[pos+1....n].
For now we have array b[] and we need to know how many balls will disappear. The problem statement gives us an important clue: no 3 balls will initially have the same color. This means, any time, at most one contiguous range of balls of same color will exist with length at least 3. If it exists, we have to remove it. Then, we have to repeat this process.
So algorithm is something like bubble sort: while b[] array has changed last step, continue algorithm, otherwise exit it. Now, search an i for which b[i] = b[i + 1] = b[i + 2]. Then, take the maximum j > i for which b[k] = b[i], with i < k <= j. You have to remove from b[] the subarray [i...j] and add j – i + 1 to the destroyed balls. You’ll need to return this sum – 1, because the ball you added wasn’t there at beginning. Pay attention on case when you can’t destroy anything, you need to output 0 instead of -1. There are O(n) positions where you can insert the new ball, for each of them there are maximal O(n) steps when balls are deleted and deleting balls takes maximal O(n) time, so overall complexity is O(n ^ 3).
Note: in my solution, I don’t actually do deletion. If I have to delete a range [i, j] I create a new array c[] = b[1...i – 1] + b[j+1....n] and then copy c[] into b[] array. This guarantees O(n) time for deletion.
429A - Xor-tree
There is something to learn from “propagating tree” problem, used in round #225. It’s how the special operation works. I’ll copy paste the explanation from there (with some modification, corresponding to the problem):
Let’s define level of a node the number of edges in the path from root to the node. Root (node 1) is at level 0, sons of root are at level 1, sons of sons of root are at level 2 and so on. Now suppose you want to do a special operation to a node x. What nodes from subtree of x will be flipped? Obviously, x will be first, being located at level L. Sons of x, located at level L + 1 will not be flipped. Sons of sons, located at level L + 2, will be flipped again. So, nodes from subtree of x located at levels L, L + 2, L + 4, ... will be flipped, and nodes located at levels L + 1, L + 3, L + 5 won’t be flipped. Let’s take those values of L modulo 2. All nodes having remainder L modulo 2 will be flipped, and nodes having reminder (L + 1) modulo 2 will not. In other words, for a fixed x, at a level L, let y a node from subtree of x, at level L2. If L and L2 have same parity, y will be flipped, otherwise it won’t. We’ll use this fact later. For now, let’s think what should be our first operation. Let’s consider some nodes {x1, x2, ..., xk} with property that x1 is son of x2, x2 is son of x3, ... xk-1 is son of xk and parity of levels of these nodes is the same. Suppose by now we fixed {x1, x2, ..., xk-1} (their current value is equal to their goal value), but xk is still not fixed. After some time, we’ll have to fix xk. Now, by doing this, all nodes {x1, x2, ..., xk-1} will get flipped and hence unfixed. We’ve done some useless operations, so our used strategy is not the one that gives minimal number of operations.
What we learn from this example? Suppose I want to currently fix a node X. There is no point to fix it now, unless all ancestors Y of X with property level(Y) = level(X) (mod 2) are fixed. But what if an ancestor Y of X is not fixed yet and level(Y) != level(X) (mod 2)? Can I fix node X now? The answer is yes, as future operations done on Y won’t affect X. But, by same logic, I can firstly fix Y and then fix X, because again operations done on Y won’t affect X. We get a nice property: there is no point to make an operation on a node X unless all ancestors of X are fixed.
How can we use this property? What should be the first operation? We know that node 1 is the root, hence it always won’t have any ancestor. All other nodes might have sometimes not fixed ancestors, but we know for sure, for beginning, node 1 won’t have any unfixed ancestor (because it won’t have any). So, for beginning we can start with node 1. More, suppose node 1 is unfixed. The only way to fix it is to make an operation on it. Since it’s unfixed and this is the only way to fix it, you’ll be obligated to do this operation. This means, in an optimal sequence of operations, you’ll be obligated to do this operation, too.
So, if node 1 was unfixed, we did an operation on it. If it was already fixed, we’re done with it. What are next nodes we know for sure that will have all ancestors fixed? Sons of 1, because they have only one ancestor (node 1), which we know it’s fixed. We can only fix them by doing operations of them (doing operations on node 1 / sons of them won’t affect them). Since eventually they have to be fixed and only way to be fixed is to do an operation on them, in an optimal sequence of operations, we’ll have to make operations on them. Let’s move on. What are next nodes that we know for sure all ancestors of them will be fixed? Sons of sons of 1. We can fix them by doing an operation of them, or by doing an operation on 1. But doing an operation on 1 isn’t helpful, because even if it fixes this node, it unfixes 1. Then, you’ll have to do one more operation on 1, which will unfix current node, so we do two useless operations. It turns out, the only way to fix them is to do an operation on them.
Generally, suppose all ancestors of node x are fixed. We get the current value of node x after the operations done on ancestors of x. If the current value is not the expected one, we’ll have to do an operation on node x (this is the only way to fix the node x). Now, after node x is fixed, we can process sons of it. This strategy guarantees minimal number of operations, because we do an operation only when we’re forced to do it.
This leads immediately to an O(N ^ 2) algorithm, by every time we need to do an operation to update it to nodes from its subtree. How to get O(N)? Suppose we are at node x and want to know its current value after operations done for its ancestors. Obviously, it is defined by initial value. If we know number of operations done so far by even levels for its ancestors, number of operations done so far by odd levels and current level, we can determine the current value. Suppose these values are (initial_value, odd_times, even_times, level). We observe that 2 operations cancel each other, so we can take this number modulo 2. If level mod 2 = 0, then only even_times will matter, and current_value = (initial_value + even_times) % 2. Otherwise, current_value = (initial_value + odd_times) % 2.
We can send (even_times, odd_times and level) as DFS parameters, so current_value can be calculated in O(1), and overall complexity is O(N).
429B - Working out
The particularity of this problem which makes it different by other problem of this kind is that paths need to cross exactly one cell and Iahub can go only right and down, Iahubina can go only right and up. Let's try to come up with a solution based on these facts. A good start is to analyze configurations possible for meeting cell. Iahub can come either from right or down and Iahubina can come either from right or up. However, if both Iahub and Iahubina come from right, they must have met in other cell as well before (the cell in the left of the meet one). Similarly, if one comes from up and other one from down, their paths will cross either on upper cell, lower cell or right cell.
Only 2 possible cases are: Iahub comes from right, Iahubina comes from up or Iahub comes from down, Iahubina comes from right. By drawing some skatches on paper, you'll see next cell visited after meeting one will have the same direction for both of them. More, they will never meet again. So Iahub comes from right, goes to right, Iahubina comes from up, goes to up or Iahub comes from down, goes to down and Iahubina comes from right, goes to right.
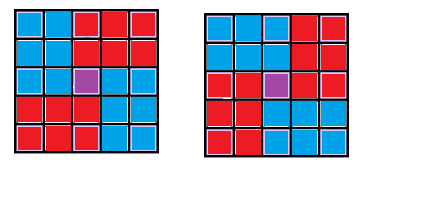
In the drawing, Iahub's possible visited cells are blue, Iahubina's possible visited cells are red and meeting cell is purple. Denote (X, Y) meeting cell.
For first case, Iahub comes from (1, 1) to (X, Y — 1) by going down or right. Next, he goes from (X, Y + 1) to (N, M) by going down or right. Iahubina goes from (M, 1) to (X + 1, Y) by going up or right and then from (X — 1, Y) to (1, M) by going with same directions. In second case, Iahub goes from (1, 1) to (X — 1, Y) and then from (X + 1, Y) to (N, M) and Iahubina goes from (M, 1) to (X, Y — 1) and then from (X, Y + 1) to (1, M).
We can precalculate for dynamic programming matrixes and we're done.
dp1[i][j] = maximal cost of a path going from (1, 1) to (i, j) only down and right.
dp2[i][j] = maximal cost of a path from (i, j) to (1, m) going only up and right.
dp3[i][j] = maximal cost of a path from (m, 1) to (i, j) going only up and right.
dp4[i][j] = maximal cost of a path from (i, j) to (n, m) going only down or right.
And here is my full implementation of recurrences (C++ only):
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
dp1[i][j] = a[i][j] + max(dp1[i - 1][j], dp1[i][j - 1]);
for (int j = m; j >= 1; --j)
for (int i = 1; i <= n; ++i)
dp2[i][j] = a[i][j] + max(dp2[i - 1][j], dp2[i][j + 1]);
for (int i = n; i >= 1; --i)
for (int j = 1; j <= m; ++j)
dp3[i][j] = a[i][j] + max(dp3[i + 1][j], dp3[i][j - 1]);
for (int i = n; i >= 1; --i)
for (int j = m; j >= 1; --j)
dp4[i][j] = a[i][j] + max(dp4[i][j + 1], dp4[i + 1][j]);Also, pay attention that meeting points can be cells (i, j) with 1 < i < n and 1 < j < m. (why?)
429C - Guess the Tree
The constrain n <= 24 immediately suggest us an exponential solution. 24 numbers seems to be not too big, but also not too small. What if we can reduce it by half? We can do this, by analyzing problem’s restriction more carefully.
The problem states that each internal node has at least two sons. After drawing some trees likes these, one may notice there are a lot of leafs in them. For a tree with this property, number of leafs is at least (n + 1) / 2. We’ll proof this affirmation by mathematical induction. For n = 1, affirmation is true. Now, suppose our tree has n nodes, and the root of it has sons {s1, s2, ..., sk}. Let’s assume subtree of s1 has n1 nodes, subtree of s2 has n2 nodes, ..., subtree of sk has nk nodes. By induction we get that s1 has at least (n1 + 1) / 2 leafs, ..., sk has at least (nk + 1) / 2 leafs. Summing up, we get that our tree has at least (n1 + n2 + ... + nk + k) / 2 leafs. But n1 + n2 + ... + nk = n – 1. So it has at least (n + k – 1) / 2 leafs. But, by hypothesis k >= 2, so our tree has at least (n + 1) / 2 leafs.
For n = 24, there will be at least 13 leafs, so at most 11 internal nodes. It looks much better now for an exponential solution! Before presenting it, we need one more observation. Suppose we sorted c[] array decreasing. Now, the father of node i can be only one of nodes {1, 2, ..., i – 1}. Nodes {i + 1, i + 2, ..., n} will have at most as much nodes as node i, so they can’t be father of i. By doing this observation we can start algorithm: start with node 1 and assign its sons. Then, move to node 2. If it does not have a father, we won’t have one, so current configuration is good. If he has a father (in this case node 1), then tree is connected so far. So we can assign children of node 2. Generally, if a node i does not have a father when it’s processed, it won’t have in future either. If it has, the tree is connected so far, so we add children of i.
Let’s introduce the following dynamic programming. Let dp[node][mask][leafs] = is it possible to create a tree if all nodes {1, 2, ..., node} have already a father, exactly leafs nodes don’t have one and internal nodes corresponding to 1 in bitmask mask also don’t have one? If you never heart about “bitmask” word, this problem is not good for you to start with. I recommend you problem E from round #191, where I explained more how bitmasks work. Back on the problem. If node has 1 in its bit from the mask, then we know for sure the tree can’t be built. Otherwise, let’s assign sons for node. We take all submasks of mask (number obtained by changing some bits from 1 to 0) and make sum of degrees for corresponding nodes. Denote this number as S. These are the internal nodes. How about the leafs? We need to have available L = c[node] – S – 1 leafs. If L is <= than leafs, we can use them. If L < 0, obviously we can’t build the tree. Will remain obviously leafs – L leafs. The new mask will be mask ^ submask. Also, we need to iterate to node + 1. If dp[node+1][mask ^ submask][leafs – L]. One more condition that needs to be considered: node needs to have at least 2 sons. This means L + cnt > 1 (where cnt are number of internal nodes used). When do we stop the dp? When c[nod] = 1. If mask = 0 and leafs = 0, then we can build the tree. Otherwise, we can’t.
Let’s analyze the complexity. There are O(2 ^ (n / 2)) masks, each of them has O(n) leafs, for each O(n) node. This gives O(2 ^ (n / 2) * n ^ 2) states. Apparently, iterating over all submasks gives O(2 ^ (n / 2)) time for each submask, so overall complexity should be O(4 ^ (n / 2) * n ^ 2). But this complexity is over rated. Taking all submasks for all masks takes O(3 ^ (n / 2)) time, instead of O(4 ^ (n / 2)) time. Why? Consider numbers written in base 3: for a mask and a submask we can assign 3 ternary digits to each bit:
0 if bit does not appear in mask
1 if bit appears in mask but not in submask
2 if bit appears in mask and in submask
Obviously, there are O(3 ^ (n / 2)) numbers like this and the two problems are equivalent, so this step takes O(3 ^ (n / 2)) and overall complexity is O(3 ^ (n / 2) * n ^ 2).
429D - Tricky Function
Let’s define S[i] = a[1] + a[2] + ... + a[i]. Then, f(i, j) = (i – j) ^ 2 + (S[i] – S[j]) ^ 2. Trying to minimize this function seems complicated, so we need to manipulate the formula more. We know from the maths that if f(i, j) is minimized, then also f’(i, j) = sqrt ( (i – j) ^ 2 + (S[i] – S[j]) ^ 2) is also minimized. Does this function look familiar to you? Suppose you get two points in 2D plane: one having coordinates (i, S[i]) and the other one having coordinates (j, S[j]). One can see that f’(i, j) is exactly euclidean distance of those points. So, if f’(i, j) is a distance between two points in plane, when is achieved minimal f’(i, j)? For the closest two points in plane (the points which are located at minimal distance). So, having set of points (i, S[i]), we need to compute closest two points from this plane. There is a classical algorithm that does this in O(n * logn).
429E - Points and Segments
The problem asks you to check the property for an infinity of points. Obviously, we can’t do that. However, we can observe that some contiguous ranges on OX axis have the same rx and bx values. Like a sweep line algorithm, a possible change may appear only when a new segment begins or when an old one ends. So let’s consider set of points formed by all li reunited with set of points formed by all ri. Sort the values increasing. Suppose the set looks like {x1, x2, ..., xk}. Then ranges [0, x1) [x1, x2) ... [xk-1, xk) [xk, infinity) are the only ones that need to be considered. If we can take an arbitrary point from each range and the property is respected for all points, then the drawing is good.
We need to color segments. But each segment is a reunion of ranges like the ones from above. When you color a segment, all ranges from it will be colored too. So, after coloring the segments, for each range, |number of times range was colored with blue – number of times range was colored with red| <= 1.
It’s time to think creative. We can see ranges as vertexes of a graph and segments as edges. For example, if a segment is formed by ranges {Xi, Xi+1, ..., Xj-1, Xj} we add an undirected edge from i to j + 1. We need to color the edges. We divide the graph into connected components and apply same logic for each component. Next, by graph I’ll refer to a connected graph.
Let’s assume that our graph has all degrees even. Then, it admits an eulerian cycle. Suppose {x1, x2, ..., xk} is the list of nodes from the cycle, such as x1-x2 x2-x3 ... xk-x1 are the edges of it, in this order. We apply a rule: if xi < xi+1, we color edge between xi and xi+1 in red. Otherwise, we color it in blue. What happens for a node? Whenever a “red” edge crosses it (for example edge 1-5 crosses node 4) a “blue” edge will always exist to cross it again (for example edge 6-2 crosses node 4). This is because of property of euler cycle: suppose we started from a node x and gone in “left”. We need to return to it, but the only way to do it is an edge which goes to “right”. So, when degrees of graph are all even, for every point on OX axis, difference between rx and bx will be always 0.
Let’s solve the general case now. Some nodes have odd degree. But there will always be an even number of nodes with odd degrees. Why? Suppose the property is respected for some edges added so far and now we add a new one. There are two cases:
1/ the edge connects two nodes with odd degree. in this case, the number of nodes with odd degrees decreases by 2, but its parity does not change.
2/ the edge connects one node with odd degree and one node with even degree. Now, degree of “old” odd one becomes even and degree of “old” even one becomes odd. So number of nodes with odd degrees does not change.
So suppose the nodes with odd degrees are X1 X2 ... Xk (k is even). Assume X1 < X2 < ... < Xk. If we add one more edge to each of these nodes, an euler cycle would be possible. However, we can’t “add” edges, because edges are segments from the input. But we can imagine them. Of course, this we’ll create an imbalance between red and blue edges, but let’s see how big it is. What if we add a fictive edge between X1 to X2, between X3 to X4, ..., between X(k – 1) to Xk? In this way, all those nodes will have even degree. So for each Xi (i odd) we add a dummy vertex Yi and some dummy edges from Xi to Yi and from Yi to Xi+1. Now let’s see the effect: if the fictive edges existed, the balance would be 0. But they do not exist, so one of rx or bx will decrease. So now |rx – bx| <= 1, good enough for problem’s restrictions.









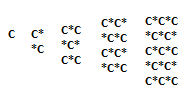



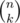 representing in how many ways I can choose k objects out of n. I have list of positions which can be transformed into fix points (they are
representing in how many ways I can choose k objects out of n. I have list of positions which can be transformed into fix points (they are 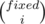 . Next, I have to fill
. Next, I have to fill 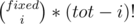 . Where is the problem to this formula?
. Where is the problem to this formula?