340A - The Wall
You are given a range [A, B]. You're asked to compute fast how many numbers in the range are divisible by both x and y. I'll present here an O(log(max(x, y)) solution. We made tests low so other not optimal solutions to pass as well. The solution refers to the original problem, where x, y ≤ 109.
Firstly, we can simplify the problem. Suppose we can calculate how many numbers are divisible in range [1, X] by both x and y. Can this solve our task? The answer is yes. All numbers in range [1, B] divisible by both numbers should be counted, except the numbers lower than A (1, 2, ..., A — 1). But, as you can see, numbers lower than A divisible by both numbers are actually numbers from range [1, A — 1]. So the answer of our task is f(B) — f(A — 1), where f(X) is how many numbers from 1, 2, ..., X are divisible by both x and y.
For calculate in O(log(max(x, y)) the f(X) we need some math. If you don't know about it, please read firstly about least common multiple. Now, what will be the lowest number divisible by both x and y. The answer is least common multiple of x and y. Let's note it by M. The sequence of the numbers divisible by both x and y is M, 2 * M, 3 * M and so on. As a proof, suppose a number z is divisible by both x and y, but it is not in the above sequence. If a number is divisible by both x and y, it will be divisible by M also. If a number is divisible by M, it will be in the above sequence. Hence, the only way a number to be divisible by both x and y is to be in sequence M, 2 * M, 3 * M, ...
The f(X) calculation reduces to finding the number of numbers from sequence M, 2 * M, 3 * M, ... lower or equal than X. It's obvious that if a number h * M is greater than X, so will be (h + 1) * M, (h + 2) * M and so on. We actually need to find the greatest integer number h such as h * M ≤ X. The numbers we're looking for will be 1 * M, 2 * M, ..., h * M (so their count will be h). The number h is actually [X / M], where [number] denotes the integer part of [number]. Take some examples on paper, you'll see why it's true.
The only thing not discussed is how to calculate the number M given 2 number x and y. You can use this formula M = x * y / gcd(x, y). For calculate gcd(x, y) you can use Euclid's algorithm. Its complexity is O(log(max(x, y)), so this is the running time for the entire algorithm.
Official solution: 4383403
340B - Maximal Area Quadrilateral
I want to apologize for not estimating the real difficulty of this task. It turns out that it was more complicated than we thought it might be. Let's start explanation.
Before reading this, you need to know what is signed area of a triangle (also called cross product or ccw function). Without it, this explanation will make no sense.
The first thing we note is that a quadrilateral self intersecting won't have maximum area. I'll show you this by an image made by my "talents" in Paint :) As you can see, if a quadrilateral self intersects, it can be transformed into one with greater area.

Each quadrilateral has 2 diagonals: connecting 1st and 3rd point and connecting 2nd and 4th point. A diagonal divides a plane into 2 subplanes. Suppose diagonal is AB. A point X can be in one of those two subplanes: that making cross product positive and that making cross product negative. A point is in "positive" subplane if ccw(X, A, B) > 0 and in "negative" subplane ccw(X, A, B) < 0. Note that according to the constraints of the task, ccw(X, A, B) will never be 0.
Let's make now the key observation of the task. We have a quadrilateral. Suppose AB is one of diagonals and C and D the other points from quadrilateral different by A and B. If the current quadrilateral could have maximal area, then one of points from C and D needs to be in "positive subplane" of AB and the other one in "negative subplane". What would happen if C and D will be in the same subplane of AB? The quadrilateral will self intersect. If it will self intersect, it won't have maximal area. "A picture is worth a thousand words" — this couldn't fit better in this case :) Note that the quadrilateral from the below image is A-C-B-D-A.

Out task reduces to fix a diagonal (this taking O(N ^ 2) time) and then choose one point from the positive and the negative subplane of the diagonal. I'll say here how to choose the point from the positive subplane. That from negative subplane can be chosen identically. The diagonal and 3rd point chosen form a triangle. As we want quadrilateral to have maximal area, we need to choose 3rd point such as triangle makes the maximal area. As the positive and negative subplanes are disjoint, the choosing 3rd point from each of them can be made independently. Hence we get O(N ^ 3) complexity. A tricky case is when you choose a diagonal but one of the subplanes is empty. In this case you have to disregard the diagonal and move to the next one.
Official solution: 4383413
340C - Tourist Problem
Despite this is a math task, the only math formula we'll use is that number of permutations with n elements is n!. From this one, we can deduce the whole task.
The average formula is sum_of_all_routes / number_of_routes. As each route is a permutation with n elements, number_of_routes is n!. Next suppose you have a permutation of a: p1, p2, …, pn. The sum for it will be p1 + |p2 – p1| + … + |pn – pn-1|. The sum of routes will be the sum for each possible permutation.
We can calculate sum_of_all routes in two steps: first time we calculate sums like “p1” and then we calculate sums like “|p2 – p1| + … + |pn – pn-1|” for every existing permutation.
First step Each element of a1, a2, …, an can appear on the first position on the routes and needs to be added as much as it appears. Suppose I fixed an element X for the first position. I can fill positions 2, 3, .., n – 1 in (n – 1)! ways. Why? It is equivalent to permuting n – 1 elements (all elements except X). So sum_of_all = a1 * (n – 1)! + a2 * (n – 1)! + … * an * (n – 1)! = (n – 1)! * (a1 + a2 + … + an).
Second step For each permutation, for each position j between 1 and n – 1 we need to compute |pj — p(j + 1)|. Similarly to first step, we observe that only elements from a can appear on consecutive positions. We fix 2 indices i and j. We’re interested in how many permutations do ai appear before aj. We fix k such as on a permutation p, ai appears on position k and aj appears on a position k + 1. In how many ways can we fix this? n – 1 ways (1, 2, …, n – 1). What’s left? A sequence of (n – 2) elements which can be permuted independently. So the sum of second step is |ai - aj| * (n – 1) * (n – 2)!, for each i != j. If I note (a1 + a2 + … + an) by S1 and |ai - aj| for each i != j by S2, the answer is (N – 1)! * S1 + (N – 1)! * S2 / N!. By a simplification, the answer is (S1 + S2) / N.
The only problem remained is how to calculate S2. Simple iteration won’t enter in time limit. Let’s think different. For each element, I need to make sum of differences between it and all smaller elements in the array a. As well, I need to make sum of all different between bigger elements than it and it. I’ll focus on the first part. I sort increasing array a. Suppose I’m at position i. I know that (i – 1) elements are smaller than ai. The difference is simply (i — 1) * ai — sum_of_elements_before_position_i. Sum of elements before position i can be computed when iterating i. Let’s call the obtained sum Sleft. I need to calculate now sum of all differences between an element and bigger elements than it. This sum is equal to Sleft. As a proof, for an element ai, calculating the difference aj — ai when aj > ai is equivalent to calculating differences between aj and a smaller element of it (in this case ai). That’s why Sleft = Sright.
As a conclusion, the answer is (S1 + 2 * Sleft) / N. For make fraction irreducible, you can use Euclid's algorithm. The complexity of the presented algorithm is O(N * logN), necessary due of sorting. Sorting can be implemented by count sort as well, having a complexity of O(maximalValue), but this is not necessary.
Official solution: 4383420
340D - Bubble Sort Graph
A good way to approach this problem is to notice that you can't build the graph. In worst case, the graph will be built in O(N2) complexity, which will time out. Also, notice that "maximal independent set" is a NP-Hard task, so even if you can build the graph you can't continue from there. So, the correct route to start is to think of graph's properties instead of building it. After sketching a little on the paper, you should find this property:
Lemma 1 Suppose we choose 2 indices i and j, such as i < j. We'll have an edge on the graph between vertices ai and aj if and only if ai > aj. We'll call that i and j form an inversion in the permutation.
Proof We assume we know the proof that bubble sort does sort correctly an array. To proof lemma 1, we need to show two things.
- Every inversion will be swapped by bubble sort.
- For each i < j when ai < aj, bubble sort will NOT swap this elements.
To proof 1, if bubble sort wouldn't swap an inversion, the sequence wouldn't be sorted. But we know that bubble sort always sorts a sequence, so all inversions will be swapped. Proofing 2 is trivial, just by looking at the code.
So far we've got how the graph G is constructed. Let's apply it in maximal independent set problem.
Lemma 2 A maximal independent set of graph G is a longest increasing sequence for permutation a.
Proof: Suppose we have a set of indices i1 < i2 < ... ik such as ai1, ai2, ..., aik form an independent set. Then, anyhow we'd choose d and e, there won't exist an edge between aid and aie. According to proof 1, this only happens when aid < aie. Hence, an independent set will be equivalent to an increasing sequence of permutation a. The maximal independent set is simply the maximal increasing sequence of permutation a.
The task reduces to find longest increasing sequence for permutation a. This is a classical problem which can be solved in O(N * logN). Here is an interesting discussion about how to do it.
340E - Iahub and Permutations
In this task, author's intended solution is an O(N ^ 2) dp. However, during testing Gerald fount a solution using principle of inclusion and exclusion. We've thought to keep both solutions. We're sorry if you say the problem was well-known, but for both me and the author of the task, it was first time we saw it.
Dynamic programming solution
After reading the sequence, we can find which elements are deleted. Suppose we have in a set D all deleted elements. I'll define from now on a "free position" a position which has -1 value, so it needs to be completed with a deleted element.
We observe that some elements from D can appear on all free positions of permutation without creating a fixed point. The other elements from D can appear in all free positions except one, that will create the fixed point. It's intuitive that those two "classes" don't influence in the same way the result, so they need to be treated separated.
So from here we can get the dp state. Let dp(n, k) = in how many ways can I fill (n + k) free positions, such as n elements from D can be placed anywhere in the free position and the other k elements can be placed in all free positions except one, which will create the fixed point. As we'll prove by the recurrences, we are not interested of the values from elements of D. Instead, we'll interested in their property: if they can(not) appear in all free positions.
If k = 0, the problem becomes straight-forward. The answer for dp(n, 0) will be n!, as each permutation of (n + 0) = n numbers is valid, because all numbers can appear on all free positions. We can also calculate dp(n, 1). This means we are not allowed to place an element in a position out of (n + 1) free positions. However, we can place it in the other n positions. From now we get n elements which can be placed anywhere in the n free positions left. Hence, dp(n, 1) = n! * n.
We want to calculate dp(n, k) now, k > 1. Our goal is to reduce the number k, until find something we know how to calculate. That is, when k becomes 0 or 1 problem is solved. Otherwise, we want to reduce the problem to a problem when k becomes 0 or 1. I have two cases. In a first case, I take a number from numbers which can be placed anywhere in order to reduce the numbers which can form fixed points. In the second case, I take a number from those which can form fixed points in order to make the same goal as in the first case. Let's analyze them.
Case 1. Suppose X is the first free position, such as in the set of k numbers there exist one which cannot be placed there (because it will make a fixed point). Obviously, this position exist, otherwise k = 0. Also obviously, this position will need to be completed with a term when having a solution. In this case, I complete position X with one of n numbers. This will make number equal to X from the k numbers set to become a number which can be placed anywhere. So I "loose" one number which can be placed anywhere, but I also "gain" one. As well, I loose one number which can form a fixed point.
Hence dp(n, k) += n * dp(n, k — 1).
Case 2. In this case position X will be completed with one number from the k numbers set. All numbers which can form fixed points can appear there, except number having value equal to X. So there are k — 1 of them. I choose an arbitrary number Y from those k — 1 to place on the position X. This time I "loose" two numbers which could form fixed points: X and Y. As well, I "gain" one number which can be placed anywhere: X.
Hence dp(n, k) += (k — 1) * dp(n + 1, k — 2).
TL;DR
dp[N][0]=N!
dp[N][1]=N*dp[N][0]
dp[N][K]=N*dp[N][K-1]+(K-1)*dp[N+1][K-2] for K>=2
This recurrences can be computed by classical dp or by memoization. I'll present DamianS's source, which used memoization. As you can see, it's very short and easy to implement. Link
Inclusion and exclusion principle
I'll present here an alternative to the dynamic programming solution. Let's calculate in tot the number of deleted numbers. Also, let's calculate in fixed the maximal number of fixed points a permutation can have. For calculate fixed, let's iterate with an index i each permutation position. We can have a fixed point on position i if element from position i was deleted (ai = -1) and element i does not exist in sequence a. With other words, element i was deleted and now I want to add it back on position i to obtain maximal number of fixed points.
We iterate now an index i from fixed to 0. Let sol[i] = the number of possible permutations having exactly i fixed points. Obviously, sol[0] is the answer to our problem. Let's introduce a combination 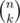 representing in how many ways I can choose k objects out of n. I have list of positions which can be transformed into fix points (they are fixed positions). I need to choose i of them. According to the above definition, I get sol[i] =
representing in how many ways I can choose k objects out of n. I have list of positions which can be transformed into fix points (they are fixed positions). I need to choose i of them. According to the above definition, I get sol[i] = 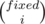 . Next, I have to fill tot - i positions with remained elements. We'll consider for this moment valid each permutation of not used values. So, sol[i] =
. Next, I have to fill tot - i positions with remained elements. We'll consider for this moment valid each permutation of not used values. So, sol[i] = 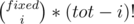 . Where is the problem to this formula?
. Where is the problem to this formula?
The problem is that it's possible, when permuting (tot — i) remained elements to be added, one (or more) elements to form more (new) fixed points. But if somehow I can exclude (subtract) the wrong choices from sol[i], sol[i] will be calculated correctly. I iterate another index j from i + 1 to fixed. For each j, I'll calculate how many permutations I considered in sol[i] having i fixed points but actually they have j. I'll subtract from sol[i] this value calculated for each j. If I do this, obviously sol[i] will be calculated correctly.
Suppose we fixed a j. We know that exactly sol[j] permutations have j fixed points (as j > i, this value is calculated correctly). Suppose now I fix a permutation having j fixed points. For get the full result, I need to calculate for all sol[j] permutations. Happily, I can multiply result obtained for a single permutation with sol[j] and obtain the result for all permutations having j fixed points. So you have a permutation having j fixed points. The problem reduces to choosing i objects from a total of j. Why? Those i objects chosen are actually the positions considered in sol[i] to be ones having exactly i fixed points. But permutation has j fixed points. Quoting for above, "For each j, I'll calculate how many permutations I considered in sol[i] having i fixed points but actually they have j" . This is exactly what algorithm does.
To sum up in a "LaTeX" way, 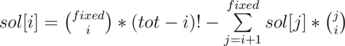
We can compute binomial coefficients using Pascal's triangle. Using inclusion and exclusion principle, we get O(N2). Please note that there exist an O(N) solution for this task, using inclusion and exclusion principle, but it's not necessary to get AC. I'll upload Gerald's source here.
341D - Iahub and Xors
The motivation of the problem is that x ^ x = 0. x ^ x ^ x… ^ x (even times) = 0
Update per range, query per element
When dealing with complicated problems, it's sometimes a good idea to try solving easier versions of them. Suppose you can query only one element each time (x0 = x1, y0 = y1).
To update a submatrix (x0, y0, x1, y1), I’ll do following operations. A[x0][y0] ^= val. A[x0][y1 + 1] ^= val. A[x1 + 1][y0] ^= val. A[x1 + 1][y1 + 1] ^= val.
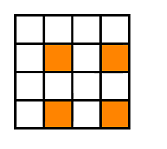
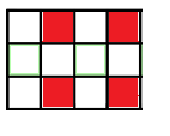
To query about an element (X, Y), that element’s value will be the xor sum of submatrix A(1, 1, X, Y). Let’s take an example. I have a 6x6 matrix and I want to xor all elements from submatrix (2, 2, 3, 4) with a value. The below image should be explanatory how the method works:

Next, by (1, 1, X, Y) I’ll denote xor sum for this submatrix.
“White” cells are not influenced by (2, 2, 3, 4) matrix, as matrix (1, 1, X, Y) with (X, Y) a white cell will never intersect it. “Red” cells are from the submatrix, the ones that need to be xor-ed. Note that for a red cell, (1, 1, X, Y) will contain the value we need to xor (as it will contain (2, 2)). Next, “blue” cells. For this ones (1, 1, X, Y) will contain the value we xor with, despite they shouldn’t have it. This is why both (2, 5) and (4, 2) will be xor-ed again by that value, to cancel the xor of (2, 2). Now it’s okay, every “blue” cell do not contain the xor value in their (1, 1, X, Y). Finally, the “green” cells. These ones are intersection between the 2 blue rectangles. This means, in their (1, 1, X, Y) the value we xor with appears 3 times (this means it is contained 1 time). For cancel this, we xor (4, 5) with the value. Now for every green cell (1, 1, X, Y) contains 4 equal values, which cancel each other.
You need a data structure do to the following 2 operations:
- Update an element (X, Y) (xor it with a value).
- Query about xor sum of (1, 1, X, Y).
Both operations can be supported by a Fenwick tree 2D. If you don't know this data structure, learn it and come back to this problem after you do this.
Coming back to our problem
Now, instead of finding an element, I want xor sum of a submatrix. You can note that xor sum of (x0, y0, x1, y1) is (1, 1, x1, y1) ^ (1, 1, x0 – 1, y1) ^ (1, 1, x1, y0 – 1) ^ (1, 1, x0 – 1, y0 – 1). This is a classical problem, the answer is (1, 1, x1, y1) from which I exclude what is not in the matrix: (1, 1, x0 – 1, y1) and (1, 1, x1, y0 – 1). Right now I excluded (1, 1, x0 – 1, y0 – 1) 2 times, so I need to add it one more time.
How to get the xor sum of submatrix (1, 1, X, Y)? In brute force approach, I’d take all elements (x, y) with 1 <= x <= X and 1 <= y <= Y and xor their values. Recall the definition of the previous problem, each element (x, y) is the xor sum of A(1, 1, x, y). So the answer is xor sum of all xor sums of A(1, 1, x, y), with 1 <= x <= X and 1 <= y <= Y.
We can rewrite that long xor sum. A number A[x][y] appears in exactly (X – x + 1) * (Y – y + 1) terms of xor sum. If (X – x + 1) * (Y – y + 1) is odd, then the value A[x][y] should be xor-ed to the final result exactly once. If (X — x + 1) * (Y — y + 1) is even, it should be ignored.
Below, you'll find 4 pictures. They are matrixes with X lines and Y columns. Each picture represents a case: (X odd, Y odd) (X even, Y even) (X even Y odd) (X odd Y even). Can you observe a nice pattern? Elements colored represent those for which (X – x + 1) * (Y – y + 1) is odd.
Yep, that's right! There are 4 cases, diving the matrix into 4 disjoint areas. When having a query of form (1, 1, X, Y) you only need specific elements sharing same parity with X and Y. This method works in O(4 * logN * logN) for each operation and is the indented solution. We keep 4 Fenwick trees 2D. We made tests such as solutions having complexity greater than O(4 * logN * logN) per operation to fail.
Here is our official solution: 4383473
341E - Candies Game
Key observation Suppose you have 3 boxes containing A, B, C candies (A, B, C all greater than 0). Then, there will be always possible to empty one of boxes using some moves.
Proof We can suppose that A <= B <= C. We need some moves such as the minimum from A, B, C will be zero. If we always keep the numbers in order A <= B <= C, it’s enough some moves such as A = 0. I’ll call this notation (A, B, C).
How can we prove that always exist such moves? We can use reductio ad absurdum to prove it. Let’s suppose, starting from (A, B, C) we can go to a state (A2, B2, C2). We suppose A2 (A2 > 0) is minimal from every state we can obtain. Since A2 is minimal number of coins that can be obtained and A2 is not zero, the statement is equivalent with we can’t empty one chest from configuration (A, B, C). Then, we can prove that from (A2, B2, C2) we can go to a state (A3, B3, C3), where A3 < A2. Obviously, this contradicts our assumption that A2 is minimal of every possible states. If A2 would be minimal, then there won’t be any series of moves to empty one chest. But A2 isn’t minimal, hence there always exist some moves to empty one chest.
Our algorithm so far:
void emptyOneBox(int A, int B, int C) {
if A is 0, then exit function.
Make some moves such as to find another state (A2, B2, C2) with A2 < A.
emptyOneBox (A2, B2, C2);
}
The only problem which needs to be proven now is: given a configuration (A, B, C) with A > 0, can we find another one (A2, B2, C2) such as A2 < A? The answer is always yes, below I’ll prove why.
Firstly, let’s imagine we want to constantly move candies into a box. It doesn't matter yet from where come the candies, what matters is candies arrive into the box. The box has initially X candies. After 1 move, it will have 2 * X candies. After 2 moves, it will have 2 * (2 * X) candies = 4 * X candies. Generally, after K moves, the box will contain 2^K * X candies.
We have A < B < C (if 2 numbers are equal, we can make a move and empty 1 box). If we divide B by A, we get from math that B = A * q + r. (obviously, always r < A). What if we can move exactly A * q candies from B to A? Then, our new state would be (r, B2, C2). We have now a number A2 = r, such as A2 < A.
How can we move exactly A * q coins? Let’s write q in base 2. Making that, q will be written as a sum of powers of 2. Suppose lim is the maximum number such as 2 ^ lim <= q. We get every number k from 0 to lim. For each k, I push into the first box (the box containing initially A candies) a certain number of candies. As proven before, I'll need to push (2 ^ k) * A candies. Let's take a look at the k-th bit from binary representation of q. If k-th bit is 1, B will be written as following: B = A * (2 ^ k + 2 ^ (other_power_1) + 2 ^ (other_power_2) + ...) + r. Hence, I'll be able to move A * (2 ^ k) candies from "B box" to "A box". Otherwise, I'll move from "C box" to "A box". It will be always possible to do this move, as C > B and I could do that move from B, too.
The proposed algorithm may look abstract, so let's take an example.
Suppose A = 3, B = 905 and C = 1024. Can we get less than 3 for this state?
B = 3 * 301 + 2. B = 3 * (100101101)2 + 2.
K = 0: we need to move (2^0) * 3 coins into A. 0th bit of q is 1, so we can move from B to A.
A = 6, B = 3 * (100101100)2 + 2 C = 1024
K = 1: we need to move (2 ^ 1) * 3 coins into A. Since 1th bit of q is already 0, we have to move from C.
A = 12, B = 3 * (100101100)2 + 2 C = 1018
K = 2: we need to move (2 ^ 2) * 3 coins into A. 2nd bit of q is 1, so we can move from B.
A = 24, B = 3 * (100101000)2 + 2 C = 1018
K = 3: we need to move (2 ^ 3) * 3 coins into A. 3nd bit of q is 1, so we can move from B.
A = 48, B = 3 * (100100000)2 + 2 C = 1018
K = 4. we need to move (2 ^ 4) * 3 coins into A. 4th bit of q is 0, we need to move from C.
A = 96, B = 3 * (100100000)2 + 2 C = 970
K = 5. we need to move (2 ^ 5) * 3 coins into A. 5th bit of q is 1, so we need to move from B.
A = 192, B = 3 * (100000000)2 + 2 C = 970
K = 6 we need to move (2 ^ 6) * 3 coins into A. We mve them from C.
A = 384 B = 3 * (100000000)2 + 2 C = 778
K = 7 we need to move (2 ^ 7) * 3 coins into A. We move them from C
A = 768 B = 3 * (100000000)2 + 2 C = 394
K=8 Finally, we can move our last 1 bit from B to A.
A = 1536 B = 3 * (000000000)2 + 2 C = 394
A = 1536 B = (3 * 0 + 2) C = 394
In the example, from (3, 905, 1024) we can arrive to (2, 394, 1536). Then, with same logic, we can go from (2, 394, 1536) to (0, X, Y), because 394 = 2 * 197 + 0.
This is how you could write emptyOneBox() procedure. The remained problem is straight-forward: if initially there are zero or one boxes having candies, the answer is "-1". Otherwise, until there are more than 2 boxes having candies, pick 3 boxes arbitrary and apply emptyOneBox().
Here is a source implementing the algorithm. 4383485
BONUS
Instead of a conclusion, I'll post here related problems to the ones used in the round. :) Please note that some of them might be more easier / complicated than level of difficulty used in the round. Feel free to think of them / ask help / discuss them in the comment section :)
Div2 A Suppose x, y, A, B ≤ 109. Instead of being asked how many bricks are colored with both red and pink in range [A, B], you're asked how many bricks are colored with at least one color. After you solve this one, solve the same problem, but instead of having 2 persons painting, you have k persons (k ≤ 20). Solution by Enchom
Div2 B Given a very long list of special points, can you find quickly a convex special quadrilateral? Can you find very very quickly? :) Also, can you find maximal area of a special convex quadrilateral in time better than O(N4)? Solutions for first problem and second problem provided by Xellos and Enchom
Div2 D / Div1 B Suppose the reverse problem. You are given a bubble sort graph having N vertices and M edges. Find its independent maximal set. Can you achieve O(N2) to do this? Does a solution in O((N + M) + N * logN) exist? Solution by CountZero
Div2 E / Div1 C Find a solution running in liniar time. Solution (dynamic programming) by ivan100sic . Solution (inclusion exclusion principle) by eduardische
Div1 D Suppose the 3D version of this problem. You have a 3D matrix and you perform same QUERY/UPDATE operations, but using 6 parameters (a submatrix is defined now all elements a[i][j][k] for which x0 <= i <= x1, y0 <= j <= y1, z0 <= k <= z1). Can you get a solution using O(log3 * N) per query, having constant 8? But for d dimensions, does an O(2d * (logd)n) algorithm per query exist? :) Solution by Dwylkz.
Div1 E In our algorithm, we pick arbitrary 3 boxes. Can you find some heuristics of picking 3 boxes to reduce number of moves?











Great! Thanks for the detailed and accurate Editorial!
Yes!
Lemma2 of 340 D is a little sudden for me.
Regarding problem D.
Well, 4 * logN * logN (nit — O() notation here is incorrect, i.e. O(10000f) = O(f)) per operation also fails if it is not Fenwick tree (e.g., 2-d segment tree). Also, it seems that even carefully implemented Fenwick solution in Java runs longer than 0.5s, so TL should be >1s. Did jury have a Java solution?
I'd like also to note that for Fenwick trees there exists a more general approach for range updates, which works, e.g., for sum instead of xor (see this post).
I've got AC with 2-D segment tree.
Does your code have complexity O(logn*logn) for queries? I always thought that 2D segment tree is O(n) for queries like (1,1,1,n)
Edit: Sorry, now I understand :D
One should distinguish 2-D segment tree and quad-tree. The first one has complexity O(logN·logN) per query, while the second one works in O(N) per query.
I implemented a quad tree and it was TLE in 6th test case. Can you help me to understand why an update or a query in a Quad tree is O(n). My solution stops the recursion when the interval asked or updated is same to the interval of the node. If you know an online explanation please share it. Thanks for the help http://codeforces.com/contest/341/submission/4390134
try querying a 1xN row. you will realize that you ultimately have to query N 1-unit squares.
Are you sure that the approach mentioned in Petr's post can be generalized to 2D or more dimensions (for supporting range updates and range queries) ?
I suppose it can: http://codeforces.com/contest/341/submission/4391440
It is interesting) It is writen in statememnt that number v from update query ≤ 262, but your solution using only int got accepted.
Maybe it's because only the parity of the number matter, so overflow doesn't affect the result?
Realizing that the "Bubble Sort Graph" problem was equivalent to finding the length of the longest increasing subsequence was a really nice "Aha!" moment for me. Great problems, thanks!
Where are the pictures in 341D?
They work perfectly for me. I uploaded them at imageshack.us . Maybe you a problem with that server. Please, tell me a server for which the images will be visible to you and I'll upload there.
Thank you for your kind reply! it's visible to me now.
For 340B I used the Gift Wrap alogirithm to compute a Convex Hull for the points, and then using a DP found the minimum Area that needs to be cut off from this Hull to form a quadrilateral.
Worst Case for Hull O(n^3) + DP O(n^2) Total execution time was 30ms
The only corner case was when the hull is composed of only 3 points.
I found that most of the solutions marked correct for the problem 340D gave the answer 1 for the input
3 12 13 1
Whereas it should have been 2(maximal set can be {12,13}). Did the test cases miss something or am I making a really silly mistake here?
Can I hack solutions after the match has ended. If so could anyone please let me know.
My bad :(. I just re-read the problem and found that the numbers can be <=n
http://codeforces.com/blog/entry/8761 PLS help!
Thanks to author for the contest. It was the best raund I have ever seen.
Can you please elaborate on how the (i — 1) * ai = sum_of_elements_before_position_i in question 341C ???
For a fixed ai, you need to calculate sum of ai — aj, when aj < ai. If I sort sequence a in increasing order, then all elements aj < ai will be in positions {1, 2, ..., i — 1}. So I need to calculate ai — a1 + ai — a2 + ... ai — a(i-1). Ai appears (i — 1) times in this sum, so I re-write the sum being (i — 1) * ai — a1 — a2 — ... — a(i — 1). This is (i — 1) * ai — (a1 + a2 + ... + a(i — 1)). I need to sum for each i this expression. It can be computed in O(N), see my source for reference. There, sumBefore is (a1 + a2 + ... + a(i — 1)).
Thanks for your reply.
Try Geogebra to draw good Geometric figures. It's free.
For 340E, can't we just do dp[n][k] = n*dp[n-1][k] + k*dp[n][k-1] ?
This is the most explanatory editorial I have ever seen on codeforces :) Really nice work guys :)
Well, turns out div2 E / div1 C has an even simpler O(N) solution. Take a look at problem-solved's elegant solution, or perhaps mine.
Just like the number of desarrangements of length n,right?
please explain the solution.
Can you please tell, what
+(i-1)*D[i-2]is needed for?I had an idea like this (which got WA, I still dont know why). Here:
BTW, my idea is:
I place i in ith position (which makes fixed point). Then for each D[i - 1] permutations, I swap i with some other number, as none of the rest will make fixed point while in ith position, and i won't make fixed point in any other position. So for each D[i - 1] (correct) permutations, I have (ends + i - 1) different numbers to swap i with and I get
D[i] = (ends+i-1)*D[i-1]. But I miss something, something withD[i-2]. :(Div2 D Bonus solution. If there is no edge between vertices ai > aj, then i > j, else i < j. One is easy to build the original sequence by applying any sorting algorithm with this comparator
solution. If there is no edge between vertices ai > aj, then i > j, else i < j. One is easy to build the original sequence by applying any sorting algorithm with this comparator
Nice solution. :) I didn't thought of that one. BTWs, for those interested there exist one way to build the sequence in linear time. You can google about research article: McConnell, Ross M.; Spinrad, Jeremy P. (1999), "Modular decomposition and transitive orientation"
Here is my solution for 341D.
Define: "sum" stand for xor sum. + , - stand for xor. a * b means that apply b + b for a - 1 times.
Notice that we could do + and - subtraction interval-wise.
But Fenwick tree could only update per range and query per element or vice versa.
If, for each element, say, ft(x, y) hold the sum of prefix sum of the matrix (1, 1, x, y) (ie. prefix sum of prefix sum of (x, y)), then for each query, ft(x1, y1) - ft(x0 - 1, y1) - ft(x1, y0 - 1) + ft(x0 - 1, y0 - 1) would be the result. As the difference between prefix-sum is the sum of the corresponding interval.
And it's easy to xor a v to elements in submatrix (x0, y0, x1, y1).
Consider 1 dimension version of this problem. For a sequence a, the prefix sum of x is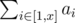 and the prefix sum of prefix sum of x is
and the prefix sum of prefix sum of x is 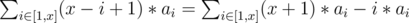 .
.
Hence, all we have to do is to maintain an extra sequnce i * ai.
Then expand method above to arbitrary dimension.
Here is an implement.
can your method also be used if we have to perform the following operations on a 2D matrix:
can the same logic be extended??
EDIT: Yes, it can be. thank you.
yes, and, it could be extended to 3 or more dimensions, too :)
Nicely written tutorial, and really good round in my opinion, looking forward for the solution of problem 341E, and also loving the idea of Bonus problems, really good authors! Thank you for the lovely round! :)
340-B maximum area quad is really tough to pass the time limit with python ! I can see no accepted solutions !!
For problem Div2 340E , in the case 2 : "Case 2. In this case position X will be completed with one number from the k numbers set..." if the position X with X is an used number, how the total number of elements which can be placed anywhere increase? For example n = 7 , -1 -1 4 2 -1 -1 -1 => N = 1 {3 } , K = 4 {1 , 5, 6, 7} , so if we put a number in K at position 2, the number of N will not increased!
X positions can be {1, 5, 6, 7}. Only those positions can create fixed points. Suppose we choose now arbitrary X = 1. I can place there numbers Y = {5, 6, 7}. Now, permutation will look like Y -1 4 2 -1 -1 -1. Obviously, 1 can be placed anywhere now, hence number N is increased.
Thank you for your answer, but I am still not clear :D
About position number 2, which case it corresponding to? like in the above case -1 Y 4 2 -1 -1 -1 -> number N will not increased.
You don't deal with it for the moment. You deal only with set of positions {1, 5, 6, 7}. Each time, you reduce one or two elements from the set (depending of choosing case 1 or case 2). When set has 0 or 1 element, then you can handle the other positions (see initialization of dp, it will handle position 2 also). As each time K decreases by 1 or 2, it's obvious sometime you'll be in the basic case, when you'll handle the other positions.
Thank you :D will need time to digest it.
I wonder if the authors will post the solutions to bonus problems after some time? :)
Anyway, here is my idea of the Div2 A — Bonus, sorry if there is much simpler solution, this is what i thought of :)
Let's say that the i-th painter will paint all bricks divisible by X[i]. I will assume that the least common multiple of X[1], X[2], X[3]...X[k] will fit in long long. (If it doesn't you can easily still solve it using the same method, it's just for the sake of simplicity). Let's define a certain colouring by a binary number. The 1s in the binary number correspond to the colors that were surely used ( 0 doesn't necessary mean the colour isn't used ). For example for K=5, 10100 would define that surely the first and third colours were used in that colouring.
To get the answer we iterate over all possible colourings, and if the colouring contains odd number of ones, we add the amount of bricks that are coloured that way, otherwise we remove that amount. The solution has complexity O(2^k*log) if implemented good, because there are 2^k possible colourings and for each we need to find the least common multiple of the used colours to determine the amount of bricks that are coloured that way.
I know it sounds quite weird and at the moment i'm struggling to find a proof, but i have tested it and it works. If someone could provide a proof that would be great :)
Yes, I'll post my ideas for Bonus tasks if there are enough persons interested. :) This is a classic task solvable by inclusion and exclusion principle. If I understood well what your solution does, it uses exactly this principle. Google it and you'll find proof for your solution :)
I'd love to see the solutions, i've spent A LOT of time on those bonus problems :).
Here is what i consider to be my "proof" for the solution i described above :P
Proof
Let's imagine we are iterating the binary numbers in order of increasing amount of ones in them. If we are for example at the number 01010, then we want to count the bricks colored that way, exactly once. However we have already counted them when looking at binary numbers 01000 and 00010. So how many times exactly have we counted a given binary number? Well if the binary number has exactly P ones in it, then we have counted it C(1,P) times when looking at numbers with 1 one in them, C(2,P) times when looking at numbers with 2 ones in them and so on. However remember that we do not always add, we subtract too, so we get the following :
For a number with P ones in it, we have counted it exactly S times where S=C(1,P)-C(2,P)+C(3,P)-C(4,P)+C(5,P)...C(P-1,P).
Well it took me quite a lot of time, but not that difficultly it can be proven that -C(0,P)+C(1,P)-C(2,P)+C(3,P)...C(P,P) equals 0, therefor obviously for odd P, S=0 and for even P — S=2. And since we want to count each colouring exactly ones, obviously for odd P, we add it once and for even P we subtract it.
C(K,N) = binomial coefficient
It's a little bit clumsy but i made it myself because i haven't heard about inclusion-exclusion principle :)
P.S. Sorry for all those long posts, i just really liked the problems and spent a lot of time on them :)
I think this is the simplest solution. It uses inclusion-exclusion principle. This problem on SPOJ
Problem 340C
I didn't understand second step to calculate sum_of_all_routes. Can someone explain with the help of example.
this step is to compute the sum of all possible differences |ai-aj| where (i != j) in all possible permutations.
consider we have the sequence a1, a2, a3, a4, a5, a6 and we want to get how many times a2 will come before a3 directly by keeping a1 a4 a5 a6 in this order as a subsequence I will list all those permutations that fullfill the last condition : a2 a3 a1 a4 a5 a6
a1 a2 a3 a4 a5 a6
a1 a4 a2 a3 a5 a6
a1 a4 a5 a2 a3 a6
a1 a4 a5 a6 a2 a3
and the number of those permutations is n-1 = 6-1 = 5. and those 5 times is when a1 a4 a5 a6 comes in this order and to compute how many times for all possible orders of a1 a4 a5 a6 then we multiply by (n-2)! = (6-2)! = 4! = 24 so the number of times that a2 a3 comes consecutivly is (n-1)*(n-2)! = (n-1)! and the sum of all differences |a2-a3| is (n-1)!*|a2-a3|. S2 is the sum of all differences |ai - aj| for each i != j .
to compute S2 : for each ai we want to compute the differece between it and all other elements aj where i != j and let us sort the given sequence a1 a2 a3 a4 a5 a6 in increasing order then the sum of all differences |ai — ak| where k<i is (i-1)*ai — (sum_of_elements_before_position_i) lets call this sum is slefti then we find slefti for each i and let sleft = sleft1 + sleft2 + sleft3 ..... + sleft6 = sum_of(slefti) for i= 1 to n when we compute sleft we find that sright = sleft where sright = sright1 + sright2 + .... + sright6 and we know that S2 = sleft + sright = 2*sleft
so the last result will be (S1 + S2) / n = (S1 + 2*sleft) / n and to make the fraction in simplest form we divide both of (S1+S2) and n on GCD((s1+s2),n)
Thanks, that was very good explaination.
Why they are dividing s2 * (n-1)! to n!? Please help me
Here is my idea on the Div2 B "Can you find maximal area convex quadrilateral", I spent a lot of time on it because it was the only problem that the author didn't have solution for :).
Its only theoretical, I haven't tested it because I am not able to write source now (I'm currently at the Balkan Olympiad), so if it is wrong please do not hate :)
My solution
Ok first, we need to find a way to check if a quadrilateral is convex while constructing it, and to do that we can simply use that quadrilateral's diagonals cross if and only if it's convex. Therefor if we find two crossing lines, created from 4 special points, we have a special convex quadrilateral.
Now as first step of our algorithm, we will take every two points and construct a line, let the points be A and B, then we will imagine its infinite continuation in the plane, and also two infinite lines perpendicular to our line and crossing it in the special points. That will divide the plane in 6 sections, but for the sake of simplicity we will look only on 3 of them (on one of the sides) because they are simetrical. Here is a picture (special points are red) :
So we have three zones, blue, green and yellow. Now let's look at all other special points that are in one of those zones. We will do a few rotating sweeping lines to have some ordered sets of points. First sweeping line will start from point A to infinite in direction opposite to B paralel to AB and save all the points in the BLUE AREA ONLY , second line will start from point A to infinite being perpendicular to AB and will save all points in the GREEN AREA ONLY, third line is the same as the second but starts from B and rotates in the opposite direction, again saves all points in the GREEN AREA ONLY, and fourth and last line is same as the first, but start from B and saves all points in the YELLOW AREA ONLY. Here is a picture of the lines and their rotating directions :
For each special point we will save the cross product it gives with line AB. So for each line we have four sets of points where the second and third actually contain the same points but with different orderings. We put those 4 sets in 4 RMQ structures so we could later get the highest of the cross products in some interval fast. Assuming we use roughly O(N*LOGN) for the sweeping lines and to build RMQ, and O(N^2) to fix a line, we have complexity of O(N^3*LOGN) for now.
Now let's proceed with our actual solution. We fix a line AB and a third point C. Now we want such point D so that AB and CD cross (being the diagonals of convex quadrilateral) and the cross product of D to the line AB is maximum. Let's look at a picture of points A,B and C :
Obviously for CD to cross AB, D must be in the area marked with white above. So now how to fast get the point with maximum cross product to AB in that white area? Well we have 3 different cases depending on the place of C in the initial 6 zones that I divided the plane into. Let's take a look.
Case 1
When C is on the other side of the blue area
So obviously we want D to be in the pink area, pink area covers part of the green and part of the yellow areas. For the green area we can use the set of points from sweeping line 2. By binary we will find the first point that is in the pink area, and then get RMQ query for that suffix of the array of points. Same thing we can do with the yellow area, using the points from sweeping line 4. Therefor we can find the best point D in O(LOGN).
Case 2
When C is on the other side of the green area
Now obviously we cover the whole green area, so we can just call a RMQ query of the whole range on any of the sweeping line 2 or 3, and for the blue part that is covered, we can again do binary and then RMQ query in points from sweep line 1, and the same thing for the yellow parts, with the points from sweep line 4.
Case 3
When C is on the other side of the yellow area
I'm not gonna show a picture of that as it is really symmetrical to case 1, you just again use binary and RMQ query in sweep lines 1 and 3 for the blue and green parts that are covered.
Obviously each test case takes roughly O(LOGN) and fixing points A,B,C is O(N^3), so i think that solution would be O(N^3*LOGN) in general. I'm sorry if it is wrong i am unable to test it right now, but I really took a lot of time to explain it nicely (sorry if it isn't very understandable), so hope I helped :)
P.S. Sorry for the long post, I was excited to share my idea :)
dude, you're awesome!
Isn't the author's solution O(N3)?
Author's solution describes a solution for finding maximal area quadrilateral, however it doesn't guarantee it will be a convex one. In the bonus tasks the author asked if anyone could find a maximal area convex quadrilateral in less than O(N^4), because he couldn't find a solution, and I took it as a challenge. It is a bonus task :)
Ah, right. I didn't notice that. Seems quite tough to implement... well done.
And a challenge atop a challenge: yesterday's gym ACM training, problem I: find the largest convex polygon which doesn't contain any of additional specified points (vertices in "red" points, doesn't contain any "blue" points).
By the way, one could use only two sweeping lines (merging 1 with 2 and 3 with 4, but you would need two binary searches for determining both ends of the interval to query about.
Also a question to the author, when you say "find a convex polygon very very fast", what complexity do you mean? The input is O(N) so I guess it's above that, but is it like O(NLOGN) or O(N^2)?
Your solution to Bonus task B is really nice :) Good job. I added it to the post.
You have to find a convex quadrilateral, not a convex polygon. And yes, this one can be done very very quick. To be precise, no matter how big is N, you can find a convex quadrilateral in O(1). Suppose you have to read also the set of points, the complexity is still O(1). I hope it does not spoil too much :)
I got it!
Among any 5 points (with any 3 non-collinear, so there are no degenerate cases), there are some 4 which form a convex quadrilateral.
Suppose we take just 4 points. Either they form a convex quadrilateral, or there's one point (P4) that's inside the triangle T (with vertices P1..3) formed by the other 3. Now, take that case.
A quad. is convex iff its diagonals intersect. So if the 5th point (P5) is outside T, then one of the triangle's sides and segment P4-P5 intersect, so there's a convex quad. defined by them.
Now, take the situation when the P5 is inside T, which is split by P4 into 3 smaller triangles (by segments P1-P4, P2-P4, P3-P4). P5 must be in one of them (w.l.o.g. in P1P2P4). And again, the segment P3-P5 must cross one of the segments P1-P4 and P2-P4, so we have a convex quadrilateral.
What we need to do is: read the first 5 points of the list, try all possible quadrilaterals formed by them and check which one (there may be more than 1, but we only need one) is convex. Since we work on N=5, time is O(1). Tada!
Yep, this is the solution :)
Anyway, this is a Ramsey theory problem, which was studied for convex N-gons also. You can read details here
Ooh, the generalization's nice! This will go to a slovak math training for sure (hehehe, let them suffer :D)!
Regarding problem C |ai - aj| for each i != j by S2, the answer is (N – 1)! * S1 + (N – 1)! * S2 / N!. In this formula i didn't understand that why they divide to N!. I will be pleasant if someone helps me.
You can use Inclusion Exclusion without all that stuff, just using the number of -1's that appeared and the number of numbers that may be fixed points...just do the math as you want to compute the derrangements and you would get something like:
this is gotta be the best tutorial of any contest of #CF ..... very nice :D (Y)
I have a qustion for B div2. Is it true, that 4 dots in the answer will be the part of convex hull?
Could anyone explain why "A number A[x][y] appears in exactly (X – x + 1) * (Y – y + 1) terms of xor sum." in Div1D problem ? What does "formula (X – x + 1)*(Y – y + 1) " mean, how we find it ?
You're interested, for each element A[x][y], how many submatrixes it influences. So, if by (1, 1, a, b) I denote xor sum of all elements in submatrix (1, 1, a, b), how many (1, 1, a, b) do contain cell (x, y)?
You can see a submatrix (1, 1, a, b) contains cell (x, y) if a >= x and b >= y. So a can be in set {x, x + 1, ...., X} and b can be in set {y, y + 1, ..., Y}. First set contains X — x + 1 values and second one contains Y — y + 1 values. Choosing a and b is independent, even if I fix an a, the b can still take any value. Using rule of product, you get the number of matrixes (1, 1, a, b) which contain (x, y) is (X — x + 1) * (Y — y + 1).
Let cnt be number of submatrixes (1, 1, a, b) which contain (x, y). If cnt is even, number cancel each other in xor sum, so no need to xor A[x][y]. If cnt is odd, exactly one A[x][y] will remain, other cnt — 1 will cancel each other, since cnt — 1 is even number.
Now saying for each cell (x, y) you xor-ed value A[x][y] each time (x, y) appears in a submatrix (1, 1, a, b) is equivalent to say for each submatrix (1, 1, a, b) you xor-ed values of all elements it contains. Is it clear why?
Yes, now it is pretty clear, I got it exactly. Thanks a lot for spending time to explain it.
Thanks a lot for this great tutorial. I am very satisfied specially at problem E of div2. The problem was fun. And so the dp solution was. :)
I think there's a minor error in BubbleSortGraph's problem statement and editorial:
It is written:
if a[i] > a[i + 1] then add an undirected edge in G between a[i] and a[i + 1]But, the edge should be between indexes i and i+1 instead of a[i] and a[i+1], consider this example:
2 3 2 6 8
The LIS here is: 2 3 6 8 , but there's an edge between 3 and 2 as indexes 2 and 3 are an inversion.
Sorry, it's correct. I didn't notice that the elements are distinct.
For 340D Bubble Sort Graph: Simple algoritham for LIS (Time complexity — O(nlogn) ) — Without using binary indexed tree,you just need to maintain one array. http://www.geeksforgeeks.org/longest-monotonically-increasing-subsequence-size-n-log-n/
Why downvotes?
My accepted solution using LIS(TC: nlogn), Without using binary indexed tree, http://codeforces.com/contest/340/submission/27713075
I couldn't understand,how 340D is related to longest increasing subsequence??? please reply me clearly .
Read lemma 2 in above editorial.
In question B, Maximum Area Quadrilateral, Can anyone explain the solution more clearly ( The image in editorial is also unavailable ) specially the corner case. Thank You
The first picture is unavailable on the editorial of 341D — Iahub and Xors. Therefore i am unable to understand the solution. Does anyone have any idea about that picture ?