(This is a beta version of editorial. It will be changed later)
I hope everybody enjoyed the contest. Here we'll present some of the author's solutions to the problems together with some other approaches that we came up with. The editorial is prepared by Lasha Lakirbaia, Anton Lomonos, and Ievgen Soboliev.
A — Game
(developed by Ievgen Soboliev & Eldar Bogdanov, editorial written by Lasha Lakirbaia)
The problem can be solved with dynamic programming technique. Let winner[a][b][move] denote who wins if both players play optimally and the first has a balls left in his box, the second has b balls left in his box and move defines who is to move next. To determine the value of winner[a][b][move], we should consider all the possible moves the next player can make and see whether any of them lead into the position winner[x][y][move2] in which this player can win with optimal play. Thus, values of winner can be defined recursively.
Ok it was a joke, the solution is just this one line: println (n1 > n2 ? “First” : “Second”).
B — Permutations
(developed by Ievgen Soboliev & Eldar Bogdanov, editorial written by Lasha Lakirbaia)
For a given array p1, p2, ..., pk let’s call the value of that expression the value of that array.
For the first subproblem, we can just consider all n! permutations in lexicographic order and keep 2 variables — one of them should be the highest value so far, and the other should be the list of permutations with that highest value. Than we can update this variables like this: When he have a new permutation, if it has smaller value, we disregard it. If it has larger value, we assign the first variable this new value and to the second variable we assign 1-element list, containing this current permutation only. In the end we just pick m-th element from the second variable. From now on we’ll concentrate on solving the harder one.
First of all let’s find out which permutations have the highest values among all the permutations of (1, 2, ..., n). It's easy to note that whenever we have some n-element array, in the highest valued permutations the position of the smallest element of the array will be either first or the last in the permutation. This can be proved easily as follows: There can't be an optimal (highest valued) permutation where the smallest element is in the middle (I mean after the first and before the last), because moving this element to either beginning or ending would obviously increase the value, that would thus contradict the statement that the original permutation had the highest value. So we proved that the position of 1 should either be at the beginning or at the end of a highest valued permutation. Moreover, it’s easy to see that in both cases, the value will be the same. After we decide on which end 1 will be, than we can move on to the remaining array (2, 3, ..., n) and do the same for 2 as we did for 1. Than we go on and do the same for 3, 4, ..., n.
From here we can clearly say what are all the permutations with the highest value — all the permutations which can be derived by the following algorithm: Consider numbers (1, 2, ..., n) in the reverse order. Each time add the current number to one of the ends of the current permutation (initially the permutation is empty). For example, for n=5 the possible permutations are (1, 2, 3, 4, 5), (1, 3, 5, 4, 2), (5, 4, 3, 2, 1) and (1, 2, 5, 4, 3). One more important thing to note is that the number of highest valued permutations of any n-element array is equal to 2n - 1, which easily follows from the way we’re constructing all these permutations. With all that said, the rest of the solution is pretty straightforward. Let’s consider numbers 1, 2, ..., n in this order and apply the following recursive approach: If we’re currently on pos-th position and searching for m-th element, having already decided the indices of all the elements less than pos, then there are 2 cases: We know that number of possible permutations is 2n - pos - 1. If m ≤ 2n - pos - 1, then we put pos element in the beginning of the array and recursively go to the state (pos + 1, m). Otherwise, we’ll put pos in the end of the array and recursively go to the state (pos + 1, 2n - pos - 1 - m). The total running time of this solution is O(n), if implemented in optimal way but almost any kind of implementation of this idea would work, as the value of n is relatively small.
Note 1: From the solution it's visible that m ≤ 249, and also for n = 50 m can be as big as 249, which doesn't fit in int but fits in long.
Note 2: This last steps can also be implemented by just considering the binary representation of m.
C — Second Price Auction
(developed by Ievgen Soboliev & Eldar Bogdanov, editorial written by Lasha Lakirbaia)
This problem can be solved in many different ways. Here we’ll explain 3 of them. Let’s denote by P(b) the probability of second highest bid being equal to b. Obviously, possible values of b are only integers from 1 to 10, 000. If we can calculate P(b) for each b in that range, then the desired expected value is just 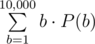 . Now let’s concentrate on calculating P(b) for a given b. These 3 solutions have different approaches to calculating the value of P(b).
. Now let’s concentrate on calculating P(b) for a given b. These 3 solutions have different approaches to calculating the value of P(b).
First solution (the easiest) — brute force
Let’s consider every partition of a set of bidders into 3 subsets, such that in the first set each bidder had higher bid than b, in second set each bid was equal to b, while in the third set each bid was less than b. As we assume that b is the second highest bid, it’s easy to notice that the first set contains either 0 or 1 element, while the second set contains at least 1 element. (Also, if the first set is empty, the second set must contain at least 2 elements) Number of such partitions is O(2n·n). After we have this partition, for each bidder we know if its bid should be more, equal or less then b. Probability of any of these can easily be counted in O(1). So in the end we get the complexity of O(2n·n·max(R - L + 1)), which is good enough for given constraints.
Second solution — dynamic programming
Let’s consider the following dynamic programming approach. Denote by (pos, moreCount, equalCount) the state, when we already considered all bidders with indices less then pos, the second largest bid in the end must be equal to b, currently the number of bidders with bid higher than b is moreCount and the number of bidders with bid equal to b is equalCount. Finally, dp(pos, moreCount, equalCount) denotes the value of P(b) for this state. Note, that we don’t have to consider the states where moreCount > 1, because for them P(b) = 0. Also, we don’t need to distinguish between states where some of them has equalCount = 2 and some of them has equalCount > 2. They have same values. So we’ll assume that equalCount < 3 and moreCount < 2.
Transitions for this dynamic programming are as follows: - Consider current bid to be higher than b. It’s only possible if moreCount = 0, because otherwise the probability of P(b) will be 0. If moreCount = 0, the transition will be to dp(pos + 1, 1, equalCount). - Consider current bid to be equal to b. It will lead us to a transition to dp(pos + 1, moreCount, min(equalCount + 1, 2)). - Consider current bid to be less than b. Transition in the case will be dp(pos + 1, moreCount, equalCount).
All these cases have their respective probabilities, which are straightforward to calculate in O(1). So as we see, the number of states of dynamic programming is O(n), while calculating each state take O(1). So in total, calculating P(b) takes O(n) time, which leads us to the solution of the initial problem in O(n * max(R - L + 1)).
Third solution — pure math
P(b) = Pr.(maxBid = b, secondMaxBid = b) + Pr.(maxBid > b, secondMaxBid = b). Let’s calculate these 2 summands separately. Denote by ri a random bid of i - th bidder.
Pr.(maxBid = b, secondMaxBid = b) = Pr.(maxBidb) - Pr.(maxBid < b) 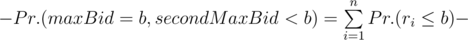
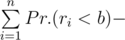
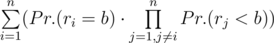 . Now let’s calculate the other summand:
. Now let’s calculate the other summand: 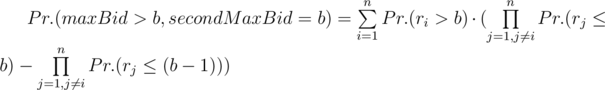 .
.
Note that each of Pr.(ri > b), Pr.(ri = b) and Pr.(ri < b) can be calculated in O(1), so P(b) can be calculated in O(n2). So in the end, we get the running time of O(n2·max(R - L + 1)). However, the last step can easily be implemented in O(n), which would give us the total running time of O(n·max(R - L + 1)), but in this problem it’s not required as n ≤ 5.
Note: As you can see, using second and third solutions the problem could be solvable for much larger values of n. However, we felt like all three approaches are equally interesting and let any of them pass. Bonus: assuming that we can multiply doubles without precision loss in polynomial time, can you solve the problem in polynomial time if the bid ranges of each company are unbounded?
D — Constrained Tree
(developed by Eldar Bogdanov, Alexander Ruff and Anton Lomonos, editorial written by Anton Lomonos)
Let's try to construct this tree from top to bottom trying to comply with given set of constraints. The first observation you need to make is if vertices i and j (i < j) should be in a given subtree then any vertex k (i < k < j) should also be in this subtree. It leads to 2 important conclusions:
- Our task "find a tree rooted at vertex 1 which should contain N vertices and comply to the given set of constraints" can be rephrased to "find a tree rooted at vertex 1 which should comply to the given set of constraints, contain the least number of vertices as possible, and contain vertex N".
- We need to know only minimums and maximums for left and right parts of each subtree.
Let's assume we are trying to construct subtree rooted at i that should contain vertex m, vertices [j1..j2] to the left of the root, and vertices [k1..k2] to the right of the root. If we don't have constraints for the left part or for the right part of the subtree then we can place all the vertices utterly to the right or to the left (we still need to check constraints for sanity). Otherwise, the conditions i < j1, j2 < k1 should take place. The vertex i + 1 should be the left child of the root. Vertices [j2 + 1;k1 - 1] may be placed to the left or to the right which depends on the constraints. Let's construct the left subtree rooted at i + 1 in such a way that it should contain the vertex j2 and contain at least number of vertices as possible. Let's assume the vertex with the biggest label in this subtree is mid. Condition mid < k1 should take place. Then we can make right child of the root to be mid + 1, and we need to construct subtree rooted at mid + 1 that should contain at least number of vertices as possible and should contain vertex max(k2, m)
The complexity of algorithm is O(N + C).
E — Subarray Cuts
(proposed by Nikhil Goyal, developed by Anton Lomonos and Lasha Lakirbaia, editorial written by Anton Lomonos and Lasha Lakirbaia)
This problem can be solved in several ways. One of the expected solution for the easier part has complexity O(n2k), which will be presented later. For now let's discuss another solution, which is also good enough for first subproblem and has complexity of O(nk2).
Let’s call the set of all possible k-tuples of partitions A; So we’re concentrating on finding the element of A with the maximal sum value. Let’s consider another set of tuples of partitions but with the following properties: We have at most k disjoint subarrays chosen. Call their sums s1, s2, …, sm (m is the number of subarrays and m ≤ k). For each 1 ≤ i ≤ (m - 1), (s(i - 1) - si) * (si - s(i + 1)) < 0. In other words, si is not between its neighbors by value. (For example, if its neighbors are 3 and 11, it will be either greater than 11 or less than 3). The number of unused (not picked) elements from the initial array is at least (k - m). In other words, we are able to add enough disjoint subarrays to this m subarrays so that in the end we have exactly k of them. Let’s call this set B.
It can be easily proved, that the maximal valued elements in A and B have the same value. The proof of this statement is given in the very end of the solution. For now let’s believe it and solve the problem.
So from now on we concentrate on finding the maximal value with the property of B.
Note that the value of any element of B with sums s1, s2, …, sm is equal to the maximum of ( + s1 - 2·s2 + 2·s3 - 2·s4 + …) and ( - s1 + 2 cdots2 - 2 cdots3 + 2·s4 - …). The important catch here is that we can ignore the property of B which says that each sum of subarray is NOT between it’s neighboring sums, because in the end we’ll get the same answers. So we just ignore that property and solve the problem without that restriction. The only restriction remaining is that they should be disjoint and the total number of unused elements should be at least (k - m). Here is the sketch of the proof why will it give the same answer: s1 - 2·s2 + 2·s3 - … = (s1 - s2) + (s3 - s2) + … ≤ |s1 - s2| + |s2 - s3| + …, as well as ( - s1 + 2·s2 - 2·s3 + ...). It means that when they’re both maximum, they equal to each other.
So we can instead concentrate on finding the maximal possible ( + s1 - 2·s2 + 2·s3 - 2·s4 + …) and ( - s1 + 2·s2 - 2·s3 + 2·s4 - …) values and it will coincide with the answer to our problem.
Denote by dp(pos, sign, first, last, unused, max) — the answer for the subproblem (apos, a(pos + 1), …) where sign means the sign of the first chosen subarray, first and last denote whether the current subarray should be first, last or none of them, unused denotes the number of unused elements that we should preserve and max denotes the maximum number of subarrays we may take. There are O(nk2) states here, cause sign, first and last each have just 2 options. Important part here is how we make transitions in O(1) and thus solve the entire problem in O(nk2). First transition would correspond to ignoring pos-th element — dp(pos + 1, sign, first, last, min(unused + 1, k), max). Otherwise we are taking apos in the first chosen subarray. There are 2 cases here: Either the current interval is just (pos, pos), or it’s length is more than 1. In the first case, the value is signapos·((firstorlast)?1: 2) + dp(pos + 1, - sign, false, 0or1, unused, max - 1). In the second case, the value would be sign·apos·((firstorlast)?1: 2) + dp(pos + 1, sign, first, last, unused, max).
Hence, in total we have 3 transitions and thus we calculate each dp(pos, sign, first, last, unused, max) in O(1). It means the entire complexity of the solution is O(nk2). Note: We didn’t present every detail and corner case, because it would be very boring to read otherwise.
Below we’ll present the solution for the harder version of this problem.
In general case we are trying to calculate this expression:
max(... + |sj - 2 - sj - 1| + |sj - 1 - sj| + |sj - sj + 1| + ...) = max(... ± (sj - 2 - sj - 1) ± (sj - 1 - sj) ± (sj - sj + 1) ± ...)
This task can be solved by using dynamic programming. Let's try to calculate recurrently the following function where we should pick subarrays j..k from array [i; n]:
f(i, j, c1, c2) = max(... ± (0 - 0) c1 (0 - sj) c2 (sj - sj + 1) ± (sj + 1 - sj + 2) ± ...), where  are defined.
are defined.
The recurrent formula for this function is:
f(i, j, c1, c2) = maxp1, p2(c1 ( - sump = p1..p2ap) c2 (sump = p1..p2ap) + f(p2 + 1, j + 1, c2, ± ))
We can easily get rid of using p1:
f(i, j, c1, c2) = max(f(i + 1, j, c1, c2), maxp2(c1 ( - sump = i..p2ap) c2 (sump = i..p2ap) + f(p2 + 1, j + 1, c2, ± ))
We can get rid from p2 by using additional function g(i, j, c1, c2), which states that subarray j already has some elements in it:
f(i, j, c1, c2) = max(f(i + 1, j, c1, c2), c1 ( - ai) c2 ai + g(i + 1, j, c1, c2))
g(i, j, c1, c2) = max(f(i, j + 1, c2, + ), f(i, j + 1, c2, - ), c1 ( - ai) c2 (ai) + g(i + 1, j, c1, c2))
There is still a matter of handling the beginning and ending of dynamic programming. There are several ways to do it. For example, we can calculate maximums and minimums of values s1 or sk based on their endings or beginnings, or we can make exceptions for using c1 and c2 if j = 1 or j = k.
The complexity of the algorithm is O(n * k).
F — Scaygerboss
(developed by Anton Lomonos, editorial written by Anton Lomonos)
The task reduces to the situation when we have k females and k males, and we need to connect them in such a way, that there will be no more than one pair in each cell. This task can be solved by using maximum flow algorithm.
Firstly we need to choose the value of our answer ans (for example, by binary search) and check if they can connect in a time no more than ans. Let's make edges of capacity 1 between source and females, between males and sink, and between inputs and outputs of each cell. Then let's make edges of capacity 1 between females and inputs of cells and between outputs of cells and males if they can reach this cell within ans (we can calculate these values by using breadth-first algorithm). If we can get a maximum flow of capacity k on this graph then they can reach each other within ans.
The above approach is enough to solve the first part of the task. It has complexity of O(k3·log(k)). For solving second part of the task one should optimize the above solution. Highly optimized solution with complexity of O(k3·log(k)) could pass, but there exists a solution with complexity O(k3).
The first observation you need to make is you don't need to reconstruct the graph each time for running maximum flow algorithm. If you run the algorithm for ans = a, and then run the algorithm for ans = b, b > a, you would just need to add additional edges and "continue to run" maximum flow algorithm. The complexity of this would be O(k3 + l·k2) where l is the number of times you do this trick. Using this observations in different ways could be enough to pass the second part of the task.
You can achieve the complexity of O(k3) by using square root decomposition. You need to divide k2 edges to k batches of k edges based on the values of ans you can use these edges for. Running maximum flow algorithm after adding each of these batches would get you O(k3) complexity. Then you know which batch would tell you what the answer is, and you run maximum flow algorithm for this batch, which is O(k3) complexity too.
You can also divide edges to batches not based by their quantities, but based by their values. You will be adding the edges of the same values to the graph in the same blow. That way your algorithm would run even faster.
I (White_Bear) would like to give special congratulations to mmaxio, Petr, niyaznigmatul, and Egor who solved F2 using Java.
G — Inversions Problem
(proposed by Ievgen Soboiliev, developed by Ievgen Soboiliev, editorial written by Lasha Lakirbaia, to be changed)
This is a draft of solution to this problem. It will be changed later. Currently it contains solutions of first 2 subproblems.
The first subproblem can be solved many ways. The easiest probably is the following: consider the dynamic programming approach where the state is (perm, m) — where perm is the current permutation and m is the number of operations that are going to be performed over it. Transitions are just all the possible permutations that can be derived in the next turns (with their respective probabilities) and obviously the other variable will be just (m - 1). The running time for this approach is O(n! * n3 * k), which is good enough for the given constraints. Note that even though for small n the number of possible permutations is pretty small and k is also small, solutions based on simulation are not working at the precision level that’s required. To solve 2 other subproblems, we are gonna need more observations. First one is the linearity of expected value. It basically means that the expected value of a sum of random variables is equal to the sum of expected values of those variables, even if they’re somehow dependent on each other. Let’s see how we can use this idea to solve this problem. For this we have to look at the number of inversions a bit differently. For each possible pair (i, j) with 1 ≤ i < j ≤ n, let’s define the random variable b(i, j) to be 0 if i - th and j - th elements will preserve the order after k operations and 1 otherwise. Now, the number of inversions in terms of these variables is equal to 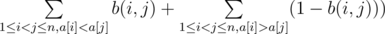 . So if we can find the expected values of each b(i, j) variables, than calculating the answer will be straightforward.
. So if we can find the expected values of each b(i, j) variables, than calculating the answer will be straightforward.
Another observation is that the expected value of a binary variables is the same as it’s probability of being equal to 1. It means that the expected value of b(i, j) is same as probability that i - th and j - th elements will swap the order in the end, after k moves.
From now on, let’s denote by p(i, j, m) the probability, that after m steps the i - th and j - th elements will swap the order (in other words, probability that the final position of the i - th element will be to the right side of the final position of j - th element). The solutions of second and third subproblems differ only in ways of calculating these values.
Easier way to find these values is to use recursive approach: Consider all the possible next moves — namely all possible intervals (x, y) on which the next step will be performed. Each of them has probability equal to 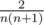 . There are several cases:
. There are several cases:
(1) Intervals (x, y) and (i, j) are either disjoint, or i < x, y < j. In both cases, the transition will be just p(i, j, m - 1).
(2) x ≤ i ≤ y < j. In this case the transition is gonna be p(x + y - i, j, m - 1).
(3) i < x ≤ j ≤ y. In this case the transition will be p(i, x + y - j, m - 1).
(4) x ≤ i ≤ j ≤ y. In this case the transition will be p(x + y - i, x + y - j, m - 1).
The running time of this solution will be O(n4 * k), which is good enough for 2-nd subproblem, but not for the third one. This solution can actually be optimized. For this, we will need to deal with above 4 cases in O(n) each, instead of O(n2).
(1) We just count how many (x, y) intervals are of this type (i < x, y < j) and than multiply this number by p(i, j, m - 1).
(2) For each fixed possible value of (x + y), count how many (x, y) exist with that sum such that x ≤ i ≤ y < j. It can easily be done in O(1). As there are O(n) possible values of (x + y), this whole step takes O(n).
(3) The approach here is exactly the same as in the second case.
(4) For each possible value of s = x + y such that x ≤ i ≤ j ≤ y and sum up (1 - p(s - j, s - i, m - 1)). There are O(n) possible values of s, so this whole step takes O(n) time.
As these 4 steps each take at most O(n), the total running time will be O(n3·k). The fastest solution works in O(n2·min(k, 2000)). This solution will be described later.










