Hi all,
I've recently come across this http://main.edu.pl/en/archive/pa/2010/fra. The problem statement is as follow: given up to n = 5000 disjoint intervals of the form [ai, bi], we let S be all the integers in these intervals (a1, a1 + 1, ..., b1, a2, ..., b2, .., bn Now, we have up to q = 500000 queries of strings, count the total number of times a string s will appear in the numbers of set S.
The only thing I can solve is if n = 1 or something, and I barely can see a way to approach this problem, especially since we can't iterate through all the intervals for each query.
If somebody could help, that would be great!
Best,
minimario









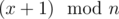 is divisible by
is divisible by 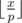 numbers divisible by
numbers divisible by 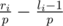 numbers divisible by
numbers divisible by 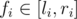 and
and 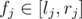 , with
, with 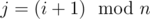 . Let
. Let 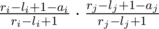 . Therefore, the probability it is can be given by
. Therefore, the probability it is can be given by 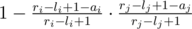 . Now, just sum over this for all
. Now, just sum over this for all 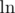 is an increasing function on positive numbers (we can see this by taking
is an increasing function on positive numbers (we can see this by taking 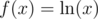 , then
, then 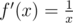 , which is positive when we are dealing with positive numbers). So if
, which is positive when we are dealing with positive numbers). So if 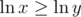 , then
, then 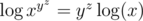 But
But 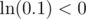 , so we cannot take another log. When can we take another log, however? We need
, so we cannot take another log. When can we take another log, however? We need 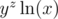 to be a positive number.
to be a positive number. 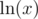 to be positive. This happens when
to be positive. This happens when 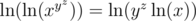 . Remember that
. Remember that 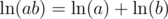 , so
, so 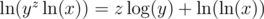 . Similarly,
. Similarly, 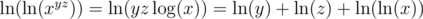 .
.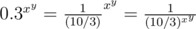 . But the denominator of this fraction is something we recognize, because
. But the denominator of this fraction is something we recognize, because 
