In a directed graph, a pair of nodes $$$(a,b)$$$ is good if we have at least:
1) One path $$$x$$$ starting at a node with indegree 0 and ending at $$$a$$$.
2) And one path $$$y$$$ starting at a node with indegree 0 and ending at $$$b$$$.
Where $$$x$$$ and $$$y$$$ don't share any node. It turns out that $$$(a,b)$$$ is not good only if:
1) At least $$$a$$$ or $$$b$$$ is/are not reachable from a node with indegree 0.
2) Or all paths which start at node with indegree 0 and end at $$$a$$$ or $$$b$$$ share at least one common node.
What is the proof of the $$$2^{nd}$$$ point?
Note: The graph can be cyclic, but no self loops or parallel edges.









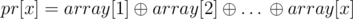 . If we divided the array into
. If we divided the array into 
