Editorial for this problem and solutions in the comments rely on a lot of symbolic expansion of various expressions until they discover regularity in formulas.
I'm used to looking at random walks as recurrences and directly solving them.
Tree below formulates the system of equations below where $$$p_i$$$ is the expectation of counts:
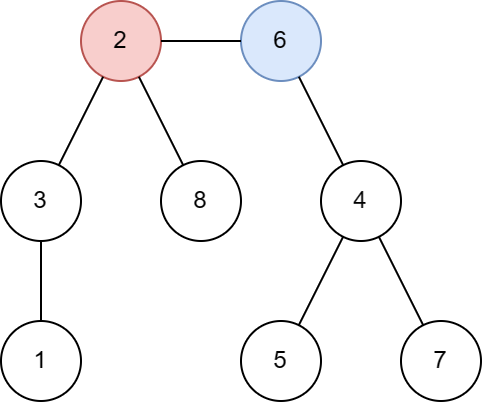
Solving general system of equations with $$$n$$$ variables is slow. I almost quit trying but this is a tree, and the rabbit out of the hat is that this sparse system can be solved by tree traversal. We start by pushing the coefficients at leaves to the parents and eventually get to the starting node (in tree above it is 2), and we can calculate the coefficient. Then a single BFS can push this information back to all nodes and calculate their expectation.
This is a general method to solve any system of equations defined by a tree.
Division is handled through pow(x, -1, M).
n, s, t, *e = map(int, open(0).read().split())
G = [[] for _ in -~n*' ']
for a, b in zip(*[iter(e)]*2):
G[a] += b,
G[b] += a,
M = 998244353
V = *C, = -~n*[0]
i = lambda x: pow(x, -1, M) # handling division as multiplication
Q = [(s, 0)] # only way to do stackless dfs in Python
while Q:
x, p = Q[-1]
if V[x]<1:
V[x] = 1
for u in G[x]:
if u!=t and u!=p: Q += (u, x),
else:
c = 0
for u in G[x]:
if u!=p and u!=t:
c = (c+C[u]*i(len(G[u])))%M
# p_i = 1/degree(child) * p_child
C[x] = i((M+1-c)*[len(G[p]), 1][p==0]) # (1 - c) * p_i = 1/degree(parent) * p_{parent}
# final coefficient C[x] is 1/((1-c)*degree(parent)) so when C[p] is materialized, multiply
Q.pop()
# C[s] is the only coefficient that is currently calculated
B = [(s, 0)] # short BFS
for x, p in B:
for u in G[x]:
if u!=t and u!=p:
C[u] = C[u]*C[x]%M
B += (u, x),
C[t] = 1
print(*C[1:])
P.S. Python 3.11 comes with 100000x efficient stack (cframes improvement). It will be possible to write a much shorter implementation with recursive DFS.












