There is a couple of things about sparse tables that a lot of people I think are doing slightly wrong (including the popular reference implementation by e-maxx).

First, you don't need to precalculate and store logarithms in an array. In fact, whichever procedure compiler will pick to calculate the logarithm is probably going to be much faster than looking it up somewhere in random access memory. The optimal way would be to use __builtin_clz ("count leading zeroes") which uses a separate instruction available on most modern x86's. This way you need just 2 memory reads instead of 3, so on large arrays this should be ~1.5x faster.

Second, memory layout and the order you iterate it matters when you're building the sparse table. There is a total of $$$2 \times 2 = 4$$$ ways to do it, and only one of them results in beautiful linear passes that work 1.5-2x faster.

It's easier to implement too:

int a[maxn], mn[logn][maxn];

int rmq(int l, int r) { // [l; r)
    int t = __lg(r - l);
    return min(mn[t][l], mn[t][r - (1 << t)]);
}

// somewhere in main:
memcpy(mn[0], a, sizeof a);
for (int l = 0; l < logn - 1; l++)
    for (int i = 0; i + (2 << l) <= n; i++)
        mn[l+1][i] = min(mn[l][i], mn[l][i + (1 << l)]);

Implementation was updated (tnx BessieTheCow and plainstop):

int lg(int x) {
    return 31 - __builtin_clz(x);
}

int rmq(int l, int r) { // [l; r)
    int t = lg(r - l);
    return min(mn[l][t], mn[r - (1 << t)][t]);

Also, it's interesting that the last loop is not getting auto-vectorized by the compiler (because std::min is probably something overly complex), and replacing it with simple (x < y ? x : y) gets total speed up to ~3x if you include avx2, but I personally wouldn't do this because it looks cumbersome:

int x = mn[l][i];
int y = mn[l][i + (1 << l)];
mn[l+1][i] = (x < y ? x : y);

(Testing performed on my laptop; didn't run it on CF or other online judges.)

http://algorithmica.org/en/b-tree

Hi, it's me again. A couple of days ago I published a post about speeding up binary search by rearranging memory in a way that allows prefetching, which is basically a way of trading off memory bandwidth for latency.

As noted in the comments, it had a noisy neighbors issue when tested on online judges, as different solutions evaluating on the same machine could compete for the same memory bandwidth. The speedup was like 2x-3x (and very volatile) on Codeforces while on my laptop and my dedicated server it was 4-5x, depending on the array sizes.

And so I rewrited it using B-tree layout instead, and it worked, because it bluntly requires 4x less memory reads. It is still quite volatile on CF—compare this (6.6x) and this (5.1x)—but I've never seen it drop below 3x on adequate array sizing (yes, the title is a bit clickbaity; I think the average speedup is around 5x).

There are two implementations:

1. One is straightforward and uses nothing fancy
2. The other is compute-optimized with AVX2 instructions and is ~30% faster, but doesn't work with older hardware (notably ideone and Yandex.Contest servers)

For more details, check the article.

Also, it would be really cool if someone could figure out a way to make compiler produce an autovectorized version of the faster one, so that it could be more easily extendable. It's weird and annoying that the compiler can't produce these 3 lines of code.

https://algorithmica.org/en/eytzinger

This will probably be an hour-long read about the CPU memory model that explains 10 lines of code at the very end.

The following code is 4 to 5 times faster than calling std::lower_bound over a sorted array:

#pragma GCC optimize("O3")
#include <bits/stdc++.h>

using namespace std;

const int n = (1<<20);
const int block_size = 16;
alignas(64) int a[n], b[n+1];

int eytzinger(int i = 0, int k = 1) {
    if (k <= n) {
        i = eytzinger(i, 2 * k);
        b[k] = a[i++];
        i = eytzinger(i, 2 * k + 1);
    }
    return i;
}

int search(int x) {
    int k = 1;
    while (k <= n) {
        __builtin_prefetch(b + k * block_size);
        k = 2 * k + (b[k] < x);
    }
    k >>= __builtin_ffs(~k);
    return k;
}

tl;dr: it uses a segment tree-like cache-friendly array reordering that allows trading off memory bandwidth for latency via prefetching. Because of this, its running time could be volatile on some online judges due to "noisy neighbor" effects (see comments below).

This is technically not a drop-in replacement, since it requires some preprocessing, but I can't recall a lot of scenarios where you obtain a sorted array but can't spend linear time on preprocessing.

This method could also be used to speedup heaps, segment trees, and other static binary tree structures.

This is my repo. There are many like it, but this one is mine. My repo is my best friend. It is my life. I must master it as I must master my life. Without me, my repo is useless. Without my repo, I am useless. I must maintain my repo true. I must commit faster than my collaborator who is trying to open issue. I must assign issue to him before he assigns issue to me. I will...

I will keep my repo clean and ready, even as I am clean and ready. We will become part of each other. We will...

Before Codeforces, I swear this creed. My repo and myself are the defenders of good solutions. We are the masters of our problemset. We are the saviors of my rating. So be it, until there is no WA, but AC. Amen.

— Maintainer's Creed

Hi. I am sharing my algorithms repository to the community and calling you to test / enrich it. It is designed to be minimalistic and copy-pastable. I use it during live contests. Most of the code is not designed to be standalone — you need to copy and tweak it a bit.

So, I scraped stats.ioinformatics.org for some data to estimate the correlation between CF rating and place you get at IOI. I guess many will find these plots interesting.

I only considered contestants who had  ≥ 5 rated contests during last 2 years before 1st of August of the relevant year. Years 2013-2017 had more than 120 such contestants, but IOI '12 had only 55 and earlier IOIs had even less, so I didn't go any further.

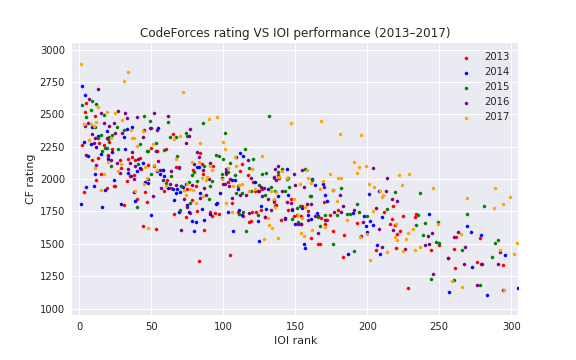
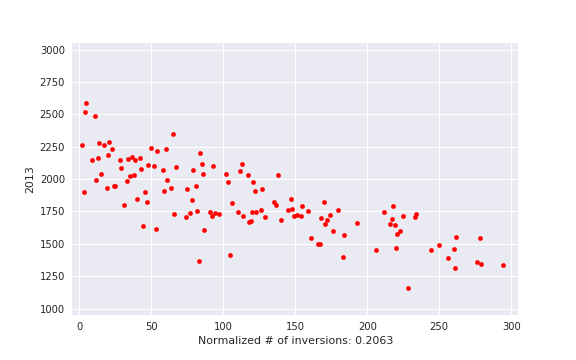
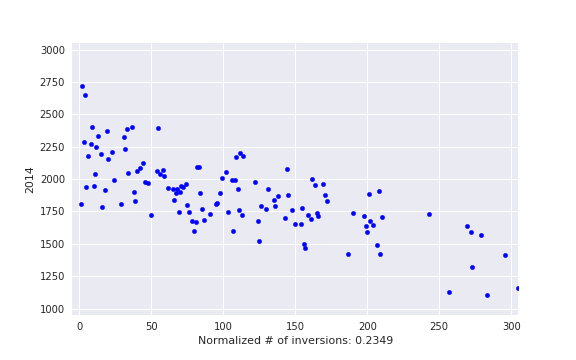
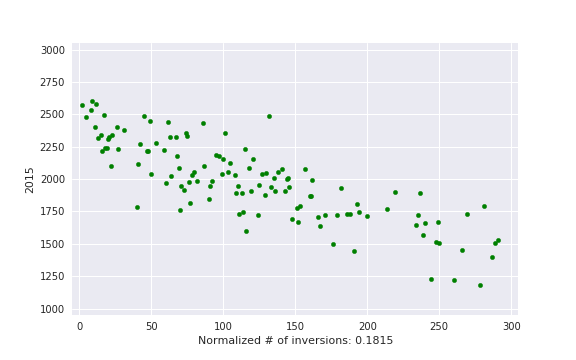
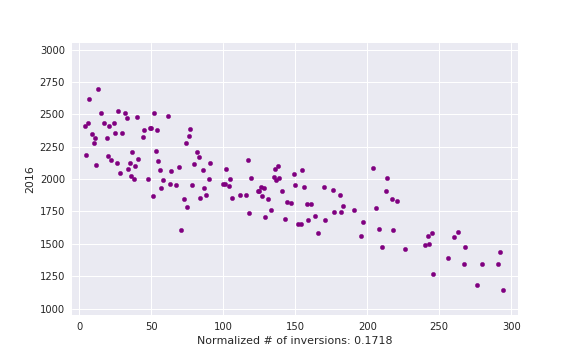
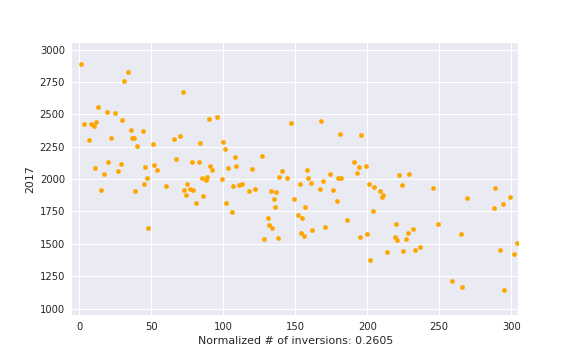
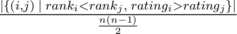By "normalized # of inversions" I mean this: , i. e. actual number of inversions divided by maximum possible. This is some kind of measure of a contest being close to a standard CF round.

For more details, check out the code: https://gist.github.com/sslotin/ae9557f68bb7e7aea1d565e2229a81c9

Most of ICPC veterans I know joined companies like Google, Facebook, Yandex or some younger tech startups (1, 2, 3) or stayed at university, getting their scientific degrees and training some high school / university students in the process. That's all quite boring. I recently found out about some unusual careers of former olympians. By "unusual" I mean something like this:

Nikolai Durov — won ICPCs of 2000 & 2001 and also performed really well at some IOIs and IMOs. He co-founded VK and Telegram. (I don't think I really needed to introduce him)

Jakub Pachocki — 2nd place at ICPC '12 and 1st at GCJ of the same year. Last month I saw him at The International presenting a Dota 2 bot by a really cool ML project

Leonid Volkov — 14th place (bronze) at ICPC '01. He went into politics and now he is the chief of staff of Alexei Navalny's campaign (he is quite a trending oppositioner in Russia)

Just for fun, what other examples do you know of?