I've spent some time on the following problem, which is quite generic (and is similar to many well-known problems):
You are given $$$2n$$$ pairs of integers $$$(x_i, y_i)$$$, where $$$1 \leq x_i, y_i \leq M$$$. Your goal is to choose exactly $$$n$$$ of them, such that their pointwise sum $$$(X, Y)$$$ (that is, you sum each coordinate on its own), minimizes the cost function $$$f(X, Y)$$$. What is the best time complexity you can achieve, given some properties about the function $$$f$$$?
Since the time complexity can depend on both $$$n$$$ and $$$M$$$, the order in which the best complexity is determined is:
Polynomial in $$$n$$$ and in $$$\log M$$$.
Polynomial in $$$n$$$ and in $$$M$$$.
$$$O(\binom{2n}{n})$$$ (applicable to all of them).
Try to solve each of the following variations, with varying difficulties. This post is purposed for all levels, and I'll try to write solutions that can be understood by all levels (except maybe for the advanced problems).
I'm interested to know if you have any other variations with interesting insights that I can add to here, as I find this topic quite interesting to research.
Problem A. $$$f(X,Y) = X + Y$$$
Problem B. $$$f$$$ can be any function
Problem C. $$$f$$$ is monotonic: for each pair of pairs $$$(x_1,y_1), (x_2, y_2)$$$ such that $$$x_1 \leq x_2$$$ and $$$y_1 \leq y_2$$$, you have $$$f(x_1, y_1) \leq f(x_2, y_2)$$$.
Problem D. $$$f(x,y) = \frac{x}{y}$$$
Problem E. $$$f(x,y) = xy$$$
Problem F. $$$f(x,y) = x^2 + y^2$$$








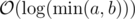 .
.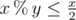 . This is due to:
. This is due to: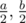 respectively. Once one of them becomes 0 the algorithm terminates, so the algorithm terminates in at most
respectively. Once one of them becomes 0 the algorithm terminates, so the algorithm terminates in at most 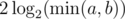 , which implies
, which implies 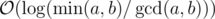
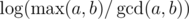 , and lastly notice that we can change the maximum to minimum, since after one step of the algorithm the current maximum is the previous minimum;
, and lastly notice that we can change the maximum to minimum, since after one step of the algorithm the current maximum is the previous minimum;  . The known time complexity analysis gives us the bound of
. The known time complexity analysis gives us the bound of 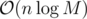 , for computing gcd
, for computing gcd 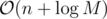 (for practical values of
(for practical values of 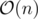 ). Why is that so? again, we can determine the time complexity more carefully:
). Why is that so? again, we can determine the time complexity more carefully: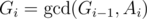
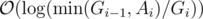 , which is worstcase
, which is worstcase 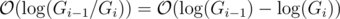 , so we will assume it's the latter.
, so we will assume it's the latter.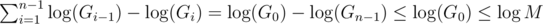
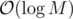 .
.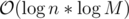 per query or update. We can use (1) to give
per query or update. We can use (1) to give 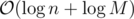 ; an update consists of a starting value, and repeatedly for
; an update consists of a starting value, and repeatedly for  steps we assign to it its gcd with some other value. Following (1), this takes the desired complexity. The same analysis is done for queries.
steps we assign to it its gcd with some other value. Following (1), this takes the desired complexity. The same analysis is done for queries.
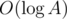 , where
, where 
