1. Clothes (A Div-2)
2. Sum of digits (B Div-2)
3. Homework (C Div-2, A Div-1)
4. Buses (D Div-2, B Div-1)
5. Vectors (E Div-2, C Div-1)
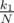 . Then average time of finding the treasure will be t1.
. Then average time of finding the treasure will be t1.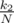 . Then average time of finding the treasure will be T1 + t2.
. Then average time of finding the treasure will be T1 + t2.
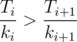 .
.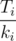 .
.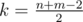 . What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m).
. What cell of board can be k-th in path? It is cell, sum of coordinate of wich is equal to k, thus, it is diagonal of doard. And then we can calculate, what maximum sum Gerald can collect, came to every cell in the diagonal, by dynamic programming in lower triangle. And the same way, we can calculate, what maximum sum Gerald can collect, came to cell (n-1,m-1), starting from every cell in the diagonal. Sumed up this to values, we calculate, what maximum sum Gerald can collect, came to from cell (0, 0) to cell (n - 1, m - 1), travel throw every cell in the diagonal. And now we will find cell (x, y), in wich maximum is reached. It is k-th cell of the path. We used time O((n + m)2) and memory O(n + m). . Four times we are find middle cell of path of length
. Four times we are find middle cell of path of length 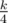 . And so on. Therefore, time of program working will be
. And so on. Therefore, time of program working will be 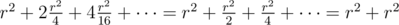 . Thus, this solution take time O((n + m)2).
. Thus, this solution take time O((n + m)2).









