The contest was postponed to 2019-01-06(Sun) 11:00-16:00 UTC.
Hello, Codeforces!
We will hold Educational DP Contest at AtCoder on Saturday.
About the Contest
This is an unofficial contest to practice DP (Dynamic Programming). We selected 26 DPs, mostly basic ones, and prepared a problem to learn each of them. Test your skills during the real contest, and brush them up after it ends.
Details
- Time (YY-MM-DD): 2019-01-06(Sun) 11:00-16:00 UTC (postponed)
- Duration: 5 hours
- Number of Tasks: 26
- Point Values: 100 points each
- Rated: No
Rules
The rules for ABC, ARC and AGC apply. The important points are:
- This is an individual match; no teams allowed.
- Revealing the solutions to others during the contest is prohibited.
- The penalty for an incorrect submission is 5 minutes.
Notices
- The problems may NOT be arranged in ascending order of difficulty.
- There are many famous problems.
- The contest is not intended for experts such as reds (anyone can compete, though).
- It is recommended to use languages that are not too slow (such as C++ and Java).











Nice idea
the problems with u all setters are that for u even div1 e problems are easy ..
so cant guess what easy means here
Don't worry, red coders are able to set up contests with easy problems.
flashback of my rounds
Okay, some red coders.
So which level are the problems in? Will the problem set be interesting for orange coders? and purple?
Since you say they are basic ones, it sounds like it should be somehow like div2 contests?
The difficulty levels of the problems range from Div2 A to Div2 E. However, it may be challenging even for Div1 coders to solve all the problems in five hours.
I get it. Thank you!
Neat idea! Are there any plans to do this with other topics as well (e.g. Educational Combinatorics contest, educational geometry contest, etc.)? I think that could be really beneficial for a lot of people, especially if this contest goes well.
Very nice initiative
Now this is some serious effort by Atcoder this year to help us strengthen up our DP. Hope they continue to come up with such good ideas.
I wanted something like this
Will an english editorial be posted when the contest ends ?
If this can be done then it will be really helpful.
Why is the contest postponed?
As mentioned in the sugim's tweet on twitter it is due to the codeforces round clashing with the atcoders' round.
"1/5 (土) 20:00 — 25:00 に開催予定の DP まとめコンテスト (https://atcoder.jp/contests/dp ) ですが、1/5 (土) 25:30 — に Codeforces のコンテストが生えたので、1/6 (日) 20:00 — 25:00 への移動を検討しています。ぜひアンケートにご協力ください。"
Nice idea to test how good you are in dp :DDD
Reminder: The contest starts in an hour.
Are questions sorted by difficulty?
and thanks for this ^^
Read the blog.
Can you please tell the approach to solve M-Candies using recursive dp ?
You have to use prefix sum concept otherwise you cant solve them within 2 secs
No the questions won't be sorted by difficulty
Difficulty according to solve count during contest: A B C D H F E I G K L M N P S O Q R J U Z Y X T V W
thanks ^^
How to solve Permutations in less than n3 ?
dp[i][j] — The number of ways to make a permutation of length i + 1 that respects the first i signs and the last element is j (j ≤ i + 1).
If s[i] is > then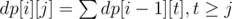
Otherwise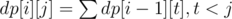
To do this in O(n2) use prefix sums
I don't really get it. Why would it be permutation? Won't we count the ways where j is used on some earlier step?
Hint: See that Rudy358 used >= instead of > in his first equation.
Ah, so we kinda insert j to the previous step permutation by increasing all the values greater or equal to j by 1 and it doesn't break anything. Yeah, that makes sense, nice.
oh wow..that's very neat trick. loved it! :D
awoo I was looking for this one line for so many days. Gods do live among us ;-; God Work Awoo
Can you please explain in detail I tried to wrap my head around this fact but I couldn't get it.
Loved the solution
dp[i][j] denotes the number of permutations of 0, 1, ..., i - 1 such that the last element is j and all the first i - 1 inequalities are fulfilled. You can easily update this dp in O(1) with prefix sums, giving O(n2) complexity.
I solved it with inclusion-exclusion principle, dividing the sequence into monotonously increasing parts. After writing down each terms, calculate dp[i] := sum of terms ending at i. That can be done in O(n^2) time. (I couldn't come up with simpler dp...)
Thanks very much for contest ! When editorial will be available ?
How to solve 0-1 Knapsack with weights <= 1e9?
In the given problem the values were ≤ 1e3, so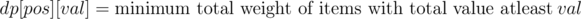 .
.
You need to make a dp[N][V] — what is the minimum weight you need to use to get the value V in the first N items. Then just iterate over the dp table to find the maximum value that requires less than W space.
Can anybody explain the solution of E for the below test case?
Problem link
Btw, there is also dp[val] solution (val<=1e5, maximum possible value) where for each i<=n check if there is j>val[i] such that adding wgh[i] to dp[j-val[i]] will minimize dp[j]. (1<=j<=val). But in order to not overlap with updates (if you go from 1 to val), either iterate from val to 1, or store all changes in vector and update it after iteration.
The contest was very nice, i didn't manage to solve quite a few problems(i got 18), which is a good thing since i will be able to solve them now and learn new things :).
How to solve Sushi?
I even don't understand it, do you?
If you have k empty piles out of n, the expected value of the number of steps to go to different state increases by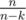 . The rest is just dp[cnt1][cnt2][cnt3] with 3 transitions.
. The rest is just dp[cnt1][cnt2][cnt3] with 3 transitions.
Hey! I am really weak at expected value problems. Can you also explain the recursive relations?
You basically have three options to pick from some state (cnt1, cnt2, cnt3). These are: eating from a pile with 3 with probability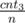 , from a pile with 2 with probability
, from a pile with 2 with probability 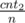 and from a pile with 1 with probability
and from a pile with 1 with probability  . So that gives you
. So that gives you
Still can't understand the recursion? :(
Can someone(awoo) please explain it?
The state is: how many piles of size 1, size 2, and size 3 there are, and E[][][] is the expected number of remaining turns. At the current step, we know each of the probabilities of picking a stone from a pile of size 1, 2, 3, or empty pile. The empty pile leads to the same state, while the others lead to states whose E[][][] value are already computed. Eventually, you will be able to solve an equation E[c1][c2][c3] = 1 + prob(empty) * E[c1][c2][c3] + (stuff in terms of previous dp values) which gives you the same formula as PikMike posted.
Yeah I understood. Thanks ksun48!
vintage_Vlad_Makeev's code helped me a lot. Very well written and self explainable.
How to calculate expected number of turns? Process for finding expected number of turns? Please explain through sample input and output
Why extra "1" is added??
Current step always uses a turn no matter what happens, the rest of the sum is the expected number of additional turns after this one.
Proof of adding 1: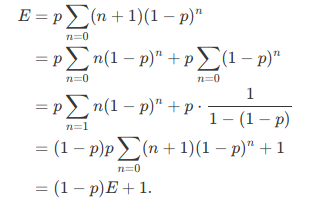
Thanks a lot, PikMike and ksun48!
Correction in what awoo posted: The probability of picking a pile with i stones should be $$$\frac{cnt_i}{cnt_1 + cnt_2 + cnt_3}$$$ given that we are only considering non empty piles now.
exactly...
Can you explain the order of iteration... unable to figure it out!!
How is the output more than 3n . For example in last test case . Since, die giving 1,2...,n have equal probabilities , each dish should be picked once in first n operations and thus each dish is picked thrice in 3n operations . And none of the dishes have more than 3 Sushies , so well how come more than 3n operations is required in some test cases ? Please help me with this :")
awoo How do you find the formula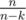 , Did you use something easier than actually evaluating arthmetic-geometric progression, (
, Did you use something easier than actually evaluating arthmetic-geometric progression, ( 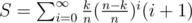 )
)
I just calculated this progression for like 100 iterations and guessed the formula. No idea about the proof.
A more intuitive way (for me) is to just write the dp as
Why extra "1" is added??
let $$$k = a + b + c$$$
$$$\mathbf{E}(a,b,c)$$$ := Expected no. of trials required to reach $$$(0,0,0)$$$ from $$$(a,b,c)$$$
$$$\mathbf{E}(a,b,c) = \frac{n-k}{n} * (1 + \mathbf{E}(a,b,c)) + \frac{a}{n} * (1 + \mathbf{E}(a-1,b,c)) + \frac{b}{n} * (1 + \mathbf{E}(a+1,b-1,c)) + \frac{c}{n} * (1 + \mathbf{E}(a,b+1,c-1))$$$ or $$$\mathbf{E}(a,b,c) = 1 + \frac{n-k}{n} * \mathbf{E}(a,b,c) + \frac{a}{n} * \mathbf{E}(a-1,b,c) + \frac{b}{n} * \mathbf{E}(a+1,b-1,c) + \frac{c}{n} * \mathbf{E}(a,b+1,c-1)$$$
hence, $$$\mathbf{E}(a,b,c) = \frac{n}{k} + \frac{a}{k} * \mathbf{E}(a-1,b,c) + \frac{b}{k} * \mathbf{E}(a+1,b-1,c) + \frac{c}{k} * \mathbf{E}(a,b+1,c-1)$$$
My understanding for the reason why we have to add 1: To reach state $$$(cnt_1, cnt_2, cnt_3)$$$ we can go from 4 states $$$(cnt_1, cnt_2, cnt_3)$$$, $$$(cnt_1-1, cnt_2, cnt_3)$$$, $$$(cnt_1+1, cnt_2-1, cnt_3)$$$ or $$$(cnt_1, cnt_2+1, cnt_3-1)$$$ with probability as above. For each "from" state, we must take the last fixed turn to reach the required state, for example if we go from $$$(cnt_1-1, cnt_2, cnt_3)$$$, we have to choose 2 for current turn. Similarly for all other states, so we add 1 because of each last fixed turn to reach our required state.
thanks.
It is well-known from statistics that for the geometric distribution (counting number of trials before a success, where each independent trial is probability p) the expected value is . In this case,
. In this case, 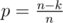 to hit a non-empty pile, so the expected value of steps to hit a non-empty pile is
to hit a non-empty pile, so the expected value of steps to hit a non-empty pile is  as desired.
as desired.
There are several ways to prove it here. Indeed, arithmetic-geometric progression is one.
What is testcase 1_03 for E?
Please share what's special in that test case,in case you come to know about it.I am also stuck only for that. Thanks in advance.
In Matching I had O(n2 * 2n ) solution, how to optimize it? I feel really stupid
You should have tried to submit it without optimization. I got AC with it in 500ms.
Well I've got TLE in last 4-5 testcases
Here is my solution
You are doing it iteratively and actually doing all 2^n * n^2 steps but many states are of no use (you will never visit them as they are not possible). If you write the same solution recursively it will pass as not all states will be visited. See: https://atcoder.jp/contests/dp/submissions/3947427
I don't think that's the case. I solved it iteratively in $$$O({2^{n}.n^{2}})$$$ with some pruning, and got it passed in $$$268ms$$$ Here's the link
EDIT : I didn't consider pruning while calculating the complexity and it's not actually $$$O({2^{n}.n^{2}})$$$. Can someone tell how to do the analysis considering pruning?
Hint: if you know mask of already paired women, you know the number of already paired men (it's just number of 1 bits in mask).
Stupid me, thank you :)
I think Expected Solution is O(n*2^n)
I hope this is the first of many Educational Rounds to come from AtCoder. Looking forward to more such good content.
Here are my solutions to the problems of this contest, in case anybody wants to refer.
You did coins but not the problems before it? Or are you still uploading problems.
Hi Nik,
I am still uploading them. :)
I solved Coins in the same way as you did but got WA. My solution What mistake did I make?
Try setting the precision to a higher number plus try putting (double) in front of every multiplication.
They mentioned absolute error actually, sad
They were checking upto 9 digits instead of the usual 6. :)
I like your idea, so i have uploaded the codes for the problems i solved. I will be adding more problems as i solve them and maybe even the explanations to some problems if i'm not too lazy.
Is CHT of Z really easier than rerooting of V or inclusion-exclusion thingy of Y?) Or is there any solution without CHT?
Btw, how does one generate tests for CHT dp? Like what stops me from maintaining MAGIC best by some parameter positions and trying to update from them all (like in O(n·MAGIC))?
Haven't even read Frog 3, the problem is actually easy with LiChao or something similar.
Yeah, I've heard that CHT is easy enough with LiChao but I've never put myself to learn it (or any other implementation of CHT). I've always thought that CHT is really advanced topic. Especially compared to problems V or Y.
LiChao is quite easy actually. I did Z with LiChao in like 10 mins while Y took me 30-40 minutes. I found Z to be easier but it may be because i practiced dp optimizations not too long ago. Didn't get to solving V during the competition.
I coded in 5 minutes but have been debugging for almost 10 minutes. Here is my code I used dynamic LiChao because I had implementation already but why it doesn't work?
Can't really tell what is wrong with your code. Here is my implementation of LiChao(The set function is nicer than in your implementation). I got it from this site. It explains quite nicely how it works and has a pretty easy to memorize implementation.
This is where I learned it from too but in my implementation, I break it to all possible cases of intersections because It is easier for me to get it right
If you have a template, (I used https://github.com/kth-competitive-programming/kactl/blob/master/content/data-structures/LineContainer.h), it's one of the easier problems.
V and Y are simpler concepts IMO but reequire more not-template code.
Well, yeah, probs. It seems I just somehow expected everyone to code all problems from scratch. :D
I really like tests for Z! (I can't come up with a MAGIC solution which passes even half of them :D) sugim48, can you please show me some generators for it?
UPD: Why did I comment that instead of writing a PM? :D
Is there an easy way to do the rerooting in V? I had to make a segment tree for every node to store the already calculated values for its neighbours to make my solution not TLE. I understand why it TLEs without the segtree but cant figure out something simpler to fix it.
You store partial products for neighbours (both prefix and suffix) and combine them to recalc the value.
Why is the limit of n so big in problem U? I spent 20 minutes trying to optimize it without realizing that O(2^32) will fit TL. Is there a faster solution?
It can be solved in O(3n) time. In fact, and there are only 3n pairs (mask, submask).
and there are only 3n pairs (mask, submask).
really nice :D
why the number of pairs of (mask, submask) is 3^n?
Consider some bit. There are 3 possibilities for it: it is equal to 1 in both mask and submask, it is equal to zero in both mask and submask and it is equal to 1 in mask and 0 in submask. So there is one-to-one correspondence between ternary masks of length n and pairs (mask, submask) of length n.
Ah I see, so there will not be case when a bit in mask is 0 whereas the bit in submask is 1 because the when the submask is 1...it automatically change the bit in mask to 1 as well (choosing the unchosen one will change the state to chosen in both masks). Is that correct?
Thanks a lot :D
Yes, that's correct.
Can someone explain the editorial of problem N,slimes?
dp[l][r] — minimum cost to merge from l to r Notice that in the last operation we will merge two consecutive blocks, and their total sum will be the sum of all slimes. So dp[l][r] = min(dp[l][k] + dp[k][r]) + a[l] + a[l + 1] + ... + a[r]. Which is O(n3)
Are you sure? The problem seems to me similar to Matrix Chain multiplication, which is O(n3) in time.
Oh I meant O(n3), my bad.
Hey, can you tell me a counter case for my algo. I trace all slimes and combine which require lease cost. And I followed this greedy technique. I cannot think of any counter test case...
420 15 10 16Minimum possible cost is 122. Your greedy approach gives 127.
How about the problem STONES
Grundy
Those who don't know about Grundy number , in brief the concept of Grundy numbers can be used to solve more general game problems in which there are N number of Piles of stones having a_1,a_2, ..... a_n stones respectively and S is a set from which players can choose a number say x and remove x number of stones from any pile (if possible) .You can read more about them here https://medium.com/@lohitmarodia/game-theory-competitive-programming-98120cc14da3 and https://www.youtube.com/watch?v=MboYbpE76js , https://www.youtube.com/watch?v=AbJqhMm8htw .
dp[i] = can we win from i stones?
Whats wrong with my approach? I have done similar recurrence in this solution
How to solve R-Walks?
B=Ak add all B[i][j]
Simple Matrix exponentiation. Find code here
can you please specify why it works? or link to any posts where it explains?
Watch this
why TLE??
https://atcoder.jp/contests/dp/submissions/3951665
The TLE is caused by visiting a state over and over.
Remember a node can have many parents.
I suggest you count the answer for each node on a topdown manner , and when visiting it again just return its value.
Can someone explain why/how Convex Hull Trick is used for Z?
We have dp[i] = min(dp[j] + (h[i] — h[j])^2) + C , (h[i] — h[j])^2 = h[i]^2 + h[j]^2 — 2*h[i]*h[j], dp[i] = min(-2*h[i]*h[j] + h[j]^2 + dp[j]) + h[i]^2 + C, the line is (-2*h[j] , h[j]^2 + dp[j]).
I did it in the same way, here is my submission but I get WA. Do you know why?
W is almost https://csacademy.com/contest/archive/task/popcorn without alien's trick (this problem is W but with positive weights and every position has an equal negative weight). I'll use this opportunity to ask: how to solve it faster than O(n * logn) with a lazy seg tree? Since O(N * log^2) is TLE for POPCORN.
https://codeforces.com/blog/entry/51880?#comment-358982
It seems that the intended solution does use the fact that the ranges only have positive weights.
Imagine my surprise there.
Any hint on Problem R(Walks) if the constraints on N would have been higher ?
With given constraints on N, it could be easily solved using Matrix Exponentiation but what if constraints on N were higher.
For small k you can find the number of walks of length k from a fixed end by making dp states as pair node index and length, for large k you might require cayley hamilton theorem. Check out this problem: https://discuss.codechef.com/questions/137912/treewalk-editorial
Oh I get, so we represent kth power Adjacency Matrix A, i.e A^k as a linear combination of I, A^1, .., A^(k-1) and solve linear recurrence using Cayley Hamilton theorem in O(N^2*log(k)), is it so?
You can simply apply Berlekamp-Massey algorithm Linear Recurrence and Berlekamp-Massey Algorithm
Can someone tell me the solution for problem X-tower and W-Intervals? I can't figure out the solution for these problems during the contest.
Problem X: Sort all blocks according to w + s decreasing. Now DP(i, j) is the maximum value of stack containing blocks for the first i blocks and current stack can contain more j unit weight.
Transition is very similar to Knapsack problem:
If we don't choose block i, then dp(i, j) -> dp(i + 1, j)
If we choose block i, then it must satisfy j >= weight[i], dp(i, j) + value[i] -> dp(i + 1, min(j — weight[i], solid[i]))
Can you prove that sort all blocks according to w + s decreasing is the right order?
Think about how you would order the blocks if there were only 2 of them, lets say the first has w1 ans s1 and the second has w2, s2. Lets consider both orderings:
If you put the first on the bottom, the strength of the tower will be s1-w2.
If you put the second on the bottom, the strength of the tower will be s2-w1.
So we want to take the first as the bottom one if s1-w2 > s2-w1.
Which is equal to saying s1+w1 > s2+w2. There you go, we want to put the ones with greater s+w on the bottom.
For more problems like this one check out these videos by Errichto: part1 part2
Why would the strength of the tower be matter?
If you want to put more blocks above the first 2, you want to make it so you can put more weight on top.
Understood, the more weight you can put on top, the change of getting optimal answer increase.
Problem W:
l[v] — left of v-th query
r[v] — right
a[v] — score for v-th query
dp[i] — answer for prefix with length i if s[i] == '1'
in naive solution dp[i] = max(dp[j] + summ(a[v])) for all j < i , for all v if l[v] <= i <= r[v] && !(l[v] <= j <= r[v]))
it works in O(n^2)
to improve it you need to use segment tree witch can give you max on prefix, for dp[i] = get(0, i — 1)
so you need to keep tree valid at each iteration
if you encountered left edge of some query make += a[v] on segment (0, l[v] — 1)
if you encountered right edge of some query make -= a[v] on segment (0, l[v] — 1)
when dp[i] is calculated += dp[i] on segment (i, i)
UPD: "r[v] — 1" to "l[v] — 1"
I think it should be: "if you encountered right edge of some query make -= a[v] on segment (0, l[v] — 1)" and not r[v]-1.
Yes, sorry, I've meant l[v] — 1
Thanks
will There be any Editorial??
I would like to request AtCoder to hold more such contests on various topics, such as one on range queries and updates, one on geometry, one on number theory and combinatorics, one on graphs, etc., similar to the dp one (where known methods are used in various ways to solve the problems).
I think this would be a great idea, helping many of us gaining the basics of topics quickly. Holding them at a every 10 days or so time interval would allow enough time to prepare the contest as well as give contestants time to upsolve the last one. I hope this is seriously considered!
Totally agree, that would be awesome :D
How can i see testcases which my solution failed in this contest.
Thanks a lot to all the authors, the problems are really exciting.
Can anybody please explain the solution for problem Y — Grid 2 as well? I'm kinda stuck. :) Basically, on how to calculate the value of so many 's when both n and r can be upto 1e5?
's when both n and r can be upto 1e5?
Editorial of this problem should be helpful: https://codeforces.com/gym/100589/problem/F
Calculating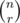 isn't hard, You just store the factorials from 1 to 105, then you can directly get required values.
isn't hard, You just store the factorials from 1 to 105, then you can directly get required values.
Yes. Realised just a few minutes after writing this comment :P.
How to solve V (Subtree)?
Let's calculate two values for every node after rooting the tree:
down[node] = number of ways to paint the descendants of node when node is black
up[node] = number of ways to paint vertices not in the subtree of node when node is black
The answer for any node is the product of these values, down[node] × up[node]
down[node] is easier to calculate, it is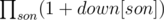 (we let the subtree rooted at son all white or we have down[son] ways). The base case is when the node is a leaf, we have 1 way to color it black.
(we let the subtree rooted at son all white or we have down[son] ways). The base case is when the node is a leaf, we have 1 way to color it black.
up[node] is almost the same, (the 1 summing in the beginning comes from letting the parent white).
(the 1 summing in the beginning comes from letting the parent white).
The trick part with up is that the modulus will not always be co-prime with the values we got (so we won't be able to calculate the inverse modular by, let's say, maintaining the product of all sons and dividing by the current son down value to get the up[node] fast). The solution is to keep a prefix and suffix product of the down values for the sons of a node, this way we don't have to divide or use modular inverses.
I am not able to figure out why this gives TLE although is running correctly for small test cases, one can guess the complexity of the above code is of order
O((V+E)*log(V+E))as the given graph is a tree , which fits in the constraints for the problem. Can you help me out?one can guess the complexity of the above code is of order O((V+E)*log(V+E)) as the given graph is a treeI am not sure this is true, for every edge you call DFS and inside the DFS you loop through every edge
for(auto i:adj[child]) {I've put my code for reference of the above explanation
Hello, everyone. Someone could explain to me how to make the problem Z — Frog 3 into something better than O (n ^ 2). Greetings and thanks in advance.
To solve it in O(n2) we have the following recurrence,
Now, hi2 + c is constant for fixed i, and we have to minimise the second term.
Now observe that the second term is of form y = mx + c, with (m, c) = ( - 2hj, hj2 + dp[j]) which we are evaluating at x = hi, which means we can use Convex Hull Trick to compute answer in O(nlogn).
Just to add so there is no confusion, it is actually dp[i] = what you wrote + dp[j]
Is there a clean way to implement the solution for U? My solution used approx.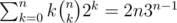 operations, which is about 4e8 when n = 16 and ran in 1.9s ( https://atcoder.jp/contests/dp/submissions/3969569 ), but I was curious if you could kick out that k factor from the sum and just get
operations, which is about 4e8 when n = 16 and ran in 1.9s ( https://atcoder.jp/contests/dp/submissions/3969569 ), but I was curious if you could kick out that k factor from the sum and just get 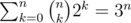 operations, which is like 4e7 on n = 16 and is much nicer.
operations, which is like 4e7 on n = 16 and is much nicer.
Yeah, check my submission: https://atcoder.jp/contests/dp/submissions/3948412. Precompute the sum for each mask to kick out the k factor.
I actually did precompute the sums for each mask; that would create a k2 factor, I believe. My k factor was coming from creating all the subset-bitmasks for a given bitmask. Your line
for (int ss = mask; ss > 0; ss = (ss - 1) & mask)is a clever way to generate them, that's pretty much exactly what I was looking for. Thanks.Yeah, that k factor comes when you are generating
next_mask.For all future readers, to understand more about how this line for generating all sub masks works -
int ss = mask; ss > 0; ss = (ss - 1) & maskYou can refer to this.
How to solve U?
You must solve the problem for each subset of the input. Since n=16, we can use bitmasks to keep a dp array of the answer for each subset. On a given subset, try each sub-subset as a potential group and recurse.
So i just watched the new episode of Algorithms live where he and his guest talked about an O(n) solution to the problem L-Deque from the dp contest. I found this very interesting and implemented it. In fact, i found it so interesting that im writing this comment to let you all know about it :)
In Matching, I failed only at one test. I could not find bug in my code. Can anyone have a look? Thanks. My submission.
Edit: I fixed it. My above code fails for the test "1 1".
does there exists better solution for O-Matching than O(2n * n2), or it was intended to pass recursive solutions, while failing iterative?
We can solve in O(2n * n) iteratively as well. We don't need the second dimension. Let k be the number of 'on' bits in the mask. dp[mask] represents number of ways in which first k men can pair with any k women subject to their preferences being matched. We can derive answer for current mask by turning off singular bits from the mask and checking compatibility of the k'th man being placed at this position.
Can someone explain the states and transitions of dp in problem T-Permutation. It got me thinking for a while now, and still don't get it. thanks in advance
Nice problems. Anyway how to solve C (vacation)?
dp[i][j] = i'm now considering the i'th day and I did the task j (A or B or C) at previous day((i-1)'th day). So I can't do the task j in this i'th day.
Can anyone explain any other approach to solving S-Digit Sum, apart from digit dp, well I'm getting a MLE by the digit-dp approach!
Or can you provide an optimization to solve my error!
My submission
Thanks in advance!
you got RE(Runtime Error) not MLE(Memory Limit Exceeded)
Try again fixing these:
num.length()can be 10001, not 1005sumis not good enough to be a DP state here as it can be big(<=9*10000) As we just only need to check "The sum of the digits in base ten is a multiple of D", instead of exact sum we can consider a statesum modulo D.startas 1? Think again.I know, 1005 was made atleast to make my code run...1e5+1 will not run the code, you'll get a compilation error :(
OK, this is naice!
start is a state which specifies whether I'm in the most significant digit of a number or not.
As far as point 1 is considered check this out
Thanks, mate I applied the point 2 optimization in my code, and it led to AC.
Thanks a ton, dude!
Here is my correct submission
How to solve M — Candies?
dp[pos][j] = number of ways of distributing j candies among [1, pos]. You can use prefix sums for transition between the states. Solution.
can you discuss in details? how the prefix sums will help
Our dp is, dp[i][j] = number of ways to distribute j candies to children from 1 to i.
Now, if we give k candies to ith child then, number of ways will be dp[i - 1][j - k].
And now, since k takes all possible values between 1 to a[i]. We have,
Now notice that j — k takes all values between [j - a[i], j - 0]. Therefore we can use prefix sums to caluculate dp[i][j] in O(1).
Now We have, dp[i][j] = prefix[i - 1][j] - prefix[i - 1][j - a[i] - 1]
Notice that we can construct prefix together with dp as,
prefix[i][j] = prefix[i][j - 1] + dp[i][j]
That works well !!
ok then.
Why O(nk) is giving TLE verdict for (M)Candies??(https://ideone.com/1wV9fq) Thanks in advance.
That's not O(nk).
Can u please tell the approach using recursive dp ?
Can anyone explain how to do O-Matching problem?
Elaborate The dp states plzz!!
F(mask) = number of ways to match all girls with 1-bit in mask with first P boys (P = number of 1-bit in mask)
Answer is: F(1111) — full mask
Transition:
F(mask) = SUM( F(submask) )
Where submask all subsets of mask without only one 1-bit (if it is possible to marrige P-th boy with this girsl)
For example:
F(1011) =
if it is possible to marrige 3-d boy with 1-st girl
F(1010) +
if it is possible to marrige 3-d boy with 2-nd girl
F(1001) +
if it is possible to marrige 3-d boy with 4-th girl
F(0011)
We try to match P-th boy to every available girl (1-bit is a free girl)
Thankss :D
Why this O(MAX_DIGIT_LENGTH * D) solution timed-out for S-Digit Sum given that MAX_DIGIT_LENGTH<=10000 and D<=100 .
UPD: Got it. :) Passing string to the function caused TLE.
Because of this: int solve( string s ,int idx,bool smaller,int rem),
add "&" here: solve( string & s ,int idx,bool smaller,int rem)
Yeah I realized that. Thanks for reply though.
Can someone elaborate how to solve Problem W — Intervals?
I tried actually
here
How to solve G?
Someone please tell
Atleast google it once, before asking for hints.
Can anyone please explain how to solve problem-W Intervals? It's been too long and i ain't able to solve it. Thanks
Can anyone help me with problem K? I have about 4 5 WAs. What's wrong with this approach?
someone explain the working of segment tree in Question W. Intervals.
Can anyone tell the idea for R-walk?
Nevermind. Got it.
Why O(nk) is giving TLE verdict for (M)Candies. https://atcoder.jp/contests/dp/submissions/4245869
Your solution is not O(nk). You are looping from 1 to a[0] and from 1 to k inside it. This can in worst case be O(k^2).
Oops...Thank you!!
how to S?
Is it possible to see test cases. I keep getting WA for last 2 cases for Digit-Sum. https://atcoder.jp/contests/dp/submissions/4247905
In res=(res-1)%mod, res can be negative. Change it to (res-1+mod)%mod
Now I get why it's better to write it as- https://ideone.com/g7Qyci
I keep on getting the wrong answer too on the last two test cases. Any suggestions for me? https://atcoder.jp/contests/dp/submissions/4755564
What is the intuition behind problem I. Coins?
On each coin, it can either come up heads or tails with certain probabilities. Make your dp state as dp[i][j] = probability of getting exactly j heads with the first i coin. Then, dp[i+1][j] will depend on dp[i][j] if we don't get heads with the i+1'th coin, or it will depend on dp[i][j-1] if we do get heads with the i+1'th coin.
Prefix dp (i.e. memoizing with the first i elements) is extremely common and probably is applied for more than half (maybe more than 3/4) of the problems in this contest. The idea of having the second dimension counting the number of heads: that's just something you would learn to see with practice.
N-Slimes i am trying to solve this question using greedy and my idea is to merge the segment based on the value of two adjacent elements sum
~~~~~
int n;cin>>n;vector<ll> v;for(int i=0;i<n;i++){int x;cin>>x;v.pb(x);}ll ans=0;for(int i=0;i<n-1;i++){int ind1=-1;int ind2=-1;ll temp=inf;for(int j=0;j<v.size()-1;j++){if(v[j]+v[j+1]<temp){temp=v[j]+v[j+1];ind1=j;ind2=j+1;}}}
cout<<ans<<endl;~~~~~ this giving WA on test 6. I know DP is the intended solution for this problem and i already solved it using DP but i can't form an edge case to convince myself that how greedy is false here, please help me to find a case where greedy fails.
3 2 2 2. Optimal way is ((3+2) + (2+2)) while your algorithm consider (3+((2+2)+2)).
I had a stream where I solved all 26 problems with explanation. You can watch it on my Youtube channel: link. There are timestamps for each problem in the pinned comment below the video.
sugim48 Any plans to have another educational on AtCoder. As you might have already realized, the DP has been a huge success. I think you (and other collaborators) may already be considering it, but I can't resist and any rough timeline will be helpful.
Hi guys, would you mind publishing the tests for the tasks?
Will there be such contests again? I know preparing and testing this lot problems requires hard work but with more people it's feasible in not much time :)
how to think this problem problem L, how to design a dp status, thanks in advance
https://atcoder.jp/contests/dp/submissions/15499385 solution for L base cases if array is of size 1 ans is a[i]
how to think -> try to make a recursive function which will take inputs as range of the array the function can be something like this
then try to optimize it i used map but it doesn't work then, eventually i found dp status which was quite easy to find after this and got AC by iterative method
need help with my solution for question Q.Flowers. Used persistent segment tree to have time limit of nlogn, but it gives TLE. Is using keyword
newso costly ? Can someone hep me optimise this code ?Similar to UVa 11790, LIS with value map
$$$dp[h]$$$ := max value LIS ending at height $$$h$$$
The key point which makes this problem solvable in $$$O(NlogN)$$$ is that heights are distinct, In the $$$O(N^2)$$$ approach,
the query of maximum is in a continuous range which should hint for using RMQ technique (like segment tree) So using segment tree we can have this in $$$O(NlogN)$$$
Solution code
How to solve U-Groupiing?
There are so many comments on this page, and multiple ones explain how to solve U.
I search for 'Grouping', and people just name U =)) thank u, i found it.
Can someone help me with the maths part in J sushi? I see the recurrence but am not very familiar with expected value so can someone elaborate it?
Here is my attempt to explain the solution in the best possible manner. Hope this will help you and others as well :)
First : what really matters is the number of dishes with 0, 1, 2 and 3 sushis and not the order of the dishes. So answer for 2,1,0,2,1 is same as answer for 0,1,1,2,2.
Number of dishes with 0 sushis is easily determined by N — one — two — three, where one is the number of dishes with 1 sushi and N is the total number of dishes in the input.
Let F(x, y, z) be the expected moves needed for x dishes with 1 sushi, y with 2 and z with 3.
Now in the next move we can pick a dish with 1 sushi with a probability of x/N or p1. we can pick a dish with 2 sushi with a probability of y/N or p2. we can pick a dish with 3 sushi with a probability of z/N or p3. we can pick a dish with 0 sushi with a probability of (N — (x + y + z))/N or p0.
Now try to understand this : F(x,y,z) = 1 + p0F(x,y,z) + p1F(x-1,y,z) + p2F(x+1,y-1,z) + p3F(x,y+1,z-1)
Here we add a 1 for the current move that we are making. (Note : if you pick a dish with 3 sushi z decreases but y increases)
This equation now becomes : (1 — p0) F(x,y,z) = 1 + p1F(x-1,y,z) + p2F(x+1,y-1,z) + p3*F(x,y+1,z-1)
simplifies to: F(x,y,z) = (1 + p1F(x-1,y,z) + p2F(x+1,y-1,z) + p3*F(x,y+1,z-1))/(1-p0)
This equation can be easily evaluated using dynamic programming :)
However try and simplify the equation to minimize the number of divisions for higher precision.
Implementation : https://atcoder.jp/contests/dp/submissions/9551520
Let me know if you find something is not clear.
thx
Yes I think I forgot to write 1 in the simplified equation.
Fixing it.
Implementation is the same thing but I have simplified the equation a little further to minimise the number of division operations.
Thanks man. I was confused with expected value. You have cleared many of my doubts.
Glad to help:)
Thanks kartik8800. Finally, I got the solution. Well explained.
I have a little doubt in the relation. Exp_val = P(x)*x, so it's the probability of that particular event multiplied by it's own frequency.
But in the recurrence relation, we are multiplying p1,p2,p3, which are the probabilities for the current state, to F(x-1,y,z) which are previous states.
What am i missing here?
I think it'll be a good idea to add the discuss button on top of this contest's page as well that links to this blog, just like other contests. It'll make the navigation easier for people trying to solve the problems to get to the discussion of solutions of the problems that are in this blog. I do think it's a very useful contest that people will be solving for a long time.
It's a shame that their is no editorial: the problems are quite educational. I think a major requirement for a contest to be educational is that it have a well-detailed editorial.
Excellent learning series !!! Would be delighted if there is a similar series on Trees & Graphs and/or an advanced DP series...
It was a nice contest for learning and practicing DP.
where do i find the editorial to this contest problems??