Model solutions are now available.
GreenGrape and I will write more about problem F, including an alternative data structures (still quite tight on time limit) ;)
1114A - Got Any Grapes?
Author: AkiLotus, GreenGrape
Development: AkiLotus, GreenGrape, neko_nyaaaaaaaaaaaaaaaaa
Editorialist: AkiLotus
First of all, we can see the grape preference is hierarchically inclusive: the grapes' types Andrew enjoys are some of those that Dmitry does, and Dmitry's favorites are included in Michal's.
Let's distribute the grapes to satisfy Andrew first, then to Dmitry, then Michal. If any of the following criteria is not satisfied (which means one of our friends is not happy), then we can immediately say that no distributions are available:
- Andrew must have at least a green grapes. So we need, x ≤ a.
- Dmitry can have purple grapes and/or the remaining green grapes. In other words, y ≤ a + b - x (the minus x is because x green grapes have been given to Andrew already).
- Michal can have grapes of any kinds. In other words, z ≤ a + b + c - x - y (similar explanations like above for both minus x and minus y).
If all three criteria are satisfied, then a grape distribution is possible.
Total complexity: 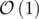 .
.
Submission link: 49737634
#pragma comment(linker, "/stack:247474112")
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
int x, y, z, a, b, c;
void Input() {
cin >> x >> y >> z;
cin >> a >> b >> c;
}
void Solve() {
if (x > a) {cout << "NO\n"; return;}
if (x + y > a + b) {cout << "NO\n"; return;}
if (x + y + z > a + b + c) {cout << "NO\n"; return;}
cout << "YES\n";
}
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0);
cin.tie(NULL); Input(); Solve();
return 0;
}
1114B - Yet Another Array Partitioning Task
Author: xuanquang1999
Development: AkiLotus, xuanquang1999
Editorialist: xuanquang1999, neko_nyaaaaaaaaaaaaaaaaa
In a perfect scenario, the maximum beauty of the original array is just a sum of m·k largest elements.
In fact, such scenario is always available regardless of the elements.
Let's denote A as the set of these m·k largest elements. The solution for us will be dividing the array into k segments, such that each segment contains exactly m elements of A. Just make a split between corresponding elements in the set A.
Depending on the way we find m·k largest elements, the time complexity might differ.
If we simply do so after sorting the entire array by usual means, the time complexity will be 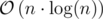 .
.
However, we can use std::nth_element function instead of sorting the entire array. The idea is to sort the array in such a way that, every elements not higher than a value v will be stored in the left side, other elements will stay on the right, and this works in linear time (a.k.a.  time complexity).
time complexity).
An example implementation of such ordering can be shown here.
Submission link: 49737896
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
int main() {
ios_base::sync_with_stdio(0); cin.tie(NULL);
int n, m, k;
cin >> n >> m >> k;
vector<pii> a(n);
for(int i = 0; i < n; ++i) {
cin >> a[i].first;
a[i].second = i;
}
sort(a.begin(), a.end(), greater<pii>());
vector<int> ind(m*k);
ll sumBeauty = 0;
for(int i = 0; i < m*k; ++i) {
sumBeauty += a[i].first;
ind[i] = a[i].second;
}
sort(ind.begin(), ind.end());
vector<int> division(k-1);
for(int i = 0; i < k-1; ++i)
division[i] = ind[(i+1)*m - 1];
cout << sumBeauty << endl;
for(int p: division)
cout << p + 1 << " ";
return 0;
}
1114C - Trailing Loves (or L'oeufs?)
Author: AkiLotus
Development: AkiLotus, majk, cdkrot
Editorialist: AkiLotus
The problem can be reduced to the following: finding the maximum r that n ! is divisible by br.
By prime factorization, we will have the following: b = p1y1·p2y2·...·pmym.
In a similar manner, we will also have: n ! = p1x1·p2x2·...·pmxm·Q (with Q being coprime to any pi presented above).
The process of finding p1, p2, ..., pm, y1, y2, ..., ym can be done by normal prime factorization of the value b.
The process of finding x1, x2, ..., xm is a little bit more tricky since the integer they were originated (n !) is too huge to be factorized manually. Still the factorial properties gave us another approach: for each pi, we can do the following:
Initially, denote xi = 0.
Repeatedly do the following: add
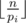 to xi, then divide n by pi. The loop ends when n is zero.
to xi, then divide n by pi. The loop ends when n is zero.
After all, we can obtain the final value r as of following: 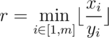 .
.
Total complexity: 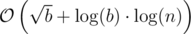 (as the number of prime factors of an integer b will not surpass
(as the number of prime factors of an integer b will not surpass 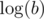 ).
).
Submission link: 49738076
#pragma comment(linker, "/stack:247474112")
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
long long n, b;
void Input() {
cin >> n >> b;
}
void Solve() {
long long ans = 1000000000000000000LL;
for (long long i=2; i<=b; i++) {
if (1LL * i * i > b) i = b;
int cnt = 0;
while (b % i == 0) {b /= i; cnt++;}
if (cnt == 0) continue;
long long tmp = 0, mul = 1;
while (mul <= n / i) {mul *= i; tmp += n / mul;}
ans = min(ans, tmp / cnt);
}
cout << ans << endl;
}
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
Input(); Solve(); return 0;
}
1114D - Flood Fill
Author: neko_nyaaaaaaaaaaaaaaaaa
Development: AkiLotus, neko_nyaaaaaaaaaaaaaaaaa, cdkrot
Editorialist: neko_nyaaaaaaaaaaaaaaaaa, cdkrot
This problem was inspired by the game Flood-it. It is apparently NP-hard. You can try out the game here. https://www.chiark.greenend.org.uk/\%7Esgtatham/puzzles/js/flood.html
The first solution is rather straightforward. Suppose squares [L, R] are flooded, then they are either of color cL or cR. We can define 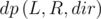 as the minimum number of moves required to make the segment [L, R] monochromic:
as the minimum number of moves required to make the segment [L, R] monochromic:
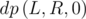 is the least moves required to make the segment having color cL.
is the least moves required to make the segment having color cL.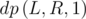 is the least moves required to make the segment having color cR.
is the least moves required to make the segment having color cR.
The second solution, which is the author's intended solution, is less so. Note that the size of the component doesn't matter, so first "compress" the array so that every adjacent elements are different. We will work on this compressed array instead.
We want to maximize the number of turns that we can fill two adjacent squares instead of one. From a starting square, this maximum number of "saved" turns is equal to the longest common subsequence (LCS) of the array expanding to the two sides. The answer is the N — (maximum LCS over all starting squares)
This is equivalent to finding the longest odd size palindrome subsequence. In fact, it is the longest palindrome subsequence. For every even-sized palindrome subsequence, since adjacent elements are different, we can just insert an element in the middle and obtain a longer palindrome subsequence.
To find the longest palindrome subsequence, we can make a reversed copy of the array and find LCS of it with the original array.
Alternatively, we can also use the first solution on the compressed array, without needing the third parameter.
Time complexity: 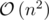 .
.
Submission link: 49738289
// Dmitry _kun_ Sayutin (2019)
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::cerr;
using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;
using std::pair;
using std::make_pair;
using std::tuple;
using std::make_tuple;
using std::get;
using std::min;
using std::abs;
using std::max;
using std::swap;
using std::unique;
using std::sort;
using std::generate;
using std::reverse;
using std::min_element;
using std::max_element;
#ifdef LOCAL
#define LASSERT(X) assert(X)
#else
#define LASSERT(X) {}
#endif
template <typename T>
T input() {
T res;
cin >> res;
LASSERT(cin);
return res;
}
template <typename IT>
void input_seq(IT b, IT e) {
std::generate(b, e, input<typename std::remove_reference<decltype(*b)>::type>);
}
#define SZ(vec) int((vec).size())
#define ALL(data) data.begin(),data.end()
#define RALL(data) data.rbegin(),data.rend()
#define TYPEMAX(type) std::numeric_limits<type>::max()
#define TYPEMIN(type) std::numeric_limits<type>::min()
int dp[5000][5000][2];
int main() {
std::iostream::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
// code here
int n = input<int>();
vector<int> a(n);
input_seq(ALL(a));
for (int i = 0; i != n; ++i)
for (int j = 0; j != n; ++j)
dp[i][j][0] = dp[i][j][1] = (i == j ? 0 : TYPEMAX(int) / 2);
for (int r = 0; r != n; ++r)
for (int l = r; l >= 0; --l)
for (int it = 0; it != 2; ++it) {
int c = (it == 0 ? a[l] : a[r]);
if (l)
dp[l - 1][r][0] = min(dp[l - 1][r][0], dp[l][r][it] + int(c != a[l - 1]));
if (r + 1 != n)
dp[l][r + 1][1] = min(dp[l][r + 1][1], dp[l][r][it] + int(c != a[r + 1]));
}
cout << min(dp[0][n - 1][0], dp[0][n - 1][1]) << "\n";
return 0;
}
Submission link: 49738394
#include <bits/stdc++.h>
using namespace std;
const int maxN = 5008;
int n;
int dp[maxN][maxN];
vector<int> a(1), b;
vector<int> ans;
void input() {
cin >> n;
for (int i = 0; i < n; i++) {
int x; cin >> x;
if (x != a.back()) a.push_back(x);
}
n = a.size() - 1;
b = a;
reverse(b.begin() + 1, b.end());
}
void solve() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i] == b[j]) {dp[i][j] = dp[i-1][j-1] + 1;}
else {dp[i][j] = max(dp[i-1][j], dp[i][j-1]);}
}
}
}
void output() {
cout << n - (dp[n][n] + 1)/2 << '\n';
}
int main() {
input();
solve();
output();
return 0;
}
1114E - Arithmetic Progression
Author: AkiLotus
Development: AkiLotus, GreenGrape
Editorialist: AkiLotus, xuanquang1999
The > query type allows you to find the max value of the array through binary searching, which will cost 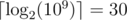 queries.
queries.
The remaining queries will be spent for the queries of the ? type to get some random elements of the array. d will be calculated as greatest common divisors of all difference between all consecutive elements, provided all elements found (yes, including the max one) is kept into a list sorted by increasing order.
Having d and max, we can easily find the min value: min = max - d·(n - 1).
The number of allowed queries seem small (30 queries to be exact), yet it's enough for us to have reasonable probability of passing the problem.
By some maths, we can find out the probability of our solution to fail being relatively small — approximately 1.86185·10 - 9.
For simplicity, assumed that the sequence a is [0, 1, 2, ..., n - 1]. Suppose that we randomly (and uniformly) select a subsequence S containing k elements from sequence a (when k is the number of ? query asked). Denote S = [s1, s2, ..., sk].
Let D the GCD of all difference between consecutive elements in S. In other word, 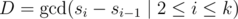 . Our solution will success if D = 1 and will fail otherwise. Let P the probability that our solution will pass (D = 1). Then the failing probability is 1 - P.
. Our solution will success if D = 1 and will fail otherwise. Let P the probability that our solution will pass (D = 1). Then the failing probability is 1 - P.
We will apply Möbius inversion to calculate P: Let f(x) the probability that D is divisible by x. Then,  (where μ(x) is the Möbius function).
(where μ(x) is the Möbius function).
Now we need to calculate f(x). It can be shown that D is divisible by x if and only if 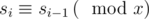 for all 2 ≤ i ≤ k. In other word, there is some r from 0 to x - 1 such that
for all 2 ≤ i ≤ k. In other word, there is some r from 0 to x - 1 such that 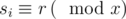 for all 1 ≤ i ≤ k.
for all 1 ≤ i ≤ k.
Let g(r) the number of ways to select a subsequence S such that 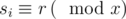 for all 1 ≤ i ≤ k. Then, according to definition:
for all 1 ≤ i ≤ k. Then, according to definition:
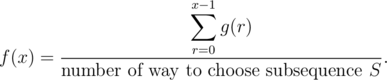
The denominator is simply  . To calculate g(r), notice that for each i, the value of si can be x·j + r for some integer j. In other word, S must be a subsequence of the sequence ar = [r, x + r, 2x + r, ...]. Let
. To calculate g(r), notice that for each i, the value of si can be x·j + r for some integer j. In other word, S must be a subsequence of the sequence ar = [r, x + r, 2x + r, ...]. Let 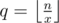 .
.
- If
 , ar has q + 1 elements. Therefore,
, ar has q + 1 elements. Therefore, 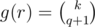
- If
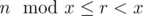 , ar has q elements. Therefore,
, ar has q elements. Therefore, 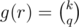 .
.
In summary:

The complexity of this calculating method is O(n). My implementation of the above method can be found here.
Keep in mind to use a good random number generator and a seed which is hard to obtain, thus making your solution truly random and not falling into corner cases.
Some of the tutorials of neal might be helpful:
Don't use rand(): a guide to random number generators in C++
How randomized solutions can be hacked, and how to make your solution unhackable
Submission link: 49739271
#pragma comment(linker, "/stack:247474112")
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
mt19937 rng32(chrono::steady_clock::now().time_since_epoch().count());
int n, Max = -1000000000, d = 0;
int queryRemaining = 60; vector<int> id;
void findMax() {
int top = -1000000000, bot = +1000000000;
while (top <= bot) {
int hasHigher;
int mid = (top + bot) / 2;
cout << "> " << mid << endl;
fflush(stdout); cin >> hasHigher;
queryRemaining--;
if (hasHigher) top = mid + 1;
else {bot = mid - 1; Max = mid;}
}
}
void findD() {
vector<int> List; int RandomRange = n;
while (queryRemaining > 0 && RandomRange > 0) {
int demandedIndex = rng32() % RandomRange;
cout << "? " << id[demandedIndex] << endl; fflush(stdout);
int z; cin >> z; List.push_back(z);
RandomRange--; queryRemaining--;
swap(id[demandedIndex], id[RandomRange]);
}
sort(List.begin(), List.end());
if (List.back() != Max) List.push_back(Max);
for (int i=1; i<List.size(); i++) {
d = __gcd(d, List[i] - List[i-1]);
}
}
void Input() {
cin >> n; id.resize(n);
for (int i=0; i<n; i++) id[i] = i+1;
}
void Solve() {
findMax(); findD();
int Min = Max - d * (n - 1);
cout << "! " << Min << " " << d;
cout << endl; fflush(stdout);
}
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0);
Input(); Solve(); return 0;
}
1114F - Please, another Queries on Array?
Author: AkiLotus, cdkrot
Development: AkiLotus, GreenGrape, cdkrot
Editorialist: AkiLotus, GreenGrape, cdkrot
There's a few fundamentals about Euler's totient we need to know:
- φ(p) = p - 1 and φ(pk) = pk - 1·(p - 1), provided p is a prime number and k is a positive integer. You can easily prove these equations through the definition of the function itself.
- Euler's totient is a multiplicative function. f(x) is considered a multiplicative function when
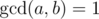 means f(a)·f(b) = f(a·b).
means f(a)·f(b) = f(a·b).
Keep in mind that we can rewrite φ(pk) as of following: 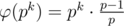 .
.
Let's denote P as the set of prime factors of 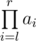 .
.
Thus, the answer for each query will simply be: 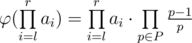 .
.
So, for each query we'll need to know the product of the elements, and which primes are included in that product.
There are a few ways to work around with it. One of the most effective way is as following:
- Create a product segment tree to maintain the segment products.
- Since
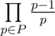 only depends on the appearance or non-appearance of the primes, and the constraints guaranteed us to have at most 62 prime factors, we can use bitmasks and an or-sum segment tree to maintain this part.
only depends on the appearance or non-appearance of the primes, and the constraints guaranteed us to have at most 62 prime factors, we can use bitmasks and an or-sum segment tree to maintain this part.
Also, the bitmasks and range products can be maintained in a sqrt-decomposition fashion (please refer to GreenGrape's solution), making each query's complexity to be somewhat around 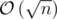 . Still, this complexity is quite high and surpassed time limit on a pretty thin margin.
. Still, this complexity is quite high and surpassed time limit on a pretty thin margin.
Complexity for initializing segment trees:  .
.
Complexity for each update query: 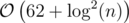 .
.
Complexity for each return query: 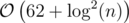 .
.
Submission link: 49739509
// Dmitry _kun_ Sayutin (2019)
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::cerr;
using std::vector;
using std::map;
using std::array;
using std::set;
using std::string;
using std::pair;
using std::make_pair;
using std::tuple;
using std::make_tuple;
using std::get;
using std::min;
using std::abs;
using std::max;
using std::swap;
using std::unique;
using std::sort;
using std::generate;
using std::reverse;
using std::min_element;
using std::max_element;
#ifdef LOCAL
#define LASSERT(X) assert(X)
#else
#define LASSERT(X) {}
#endif
template <typename T>
T input() {
T res;
cin >> res;
LASSERT(cin);
return res;
}
template <typename IT>
void input_seq(IT b, IT e) {
std::generate(b, e, input<typename std::remove_reference<decltype(*b)>::type>);
}
#define SZ(vec) int((vec).size())
#define ALL(data) data.begin(),data.end()
#define RALL(data) data.rbegin(),data.rend()
#define TYPEMAX(type) std::numeric_limits<type>::max()
#define TYPEMIN(type) std::numeric_limits<type>::min()
const int mod = 1000 * 1000 * 1000 + 7;
int add(int a, int b) {
return (a + b >= mod ? a + b - mod : a + b);
}
int sub(int a, int b) {
return (a >= b ? a - b : mod + a - b);
}
int mult(int a, int b) {
return (int64_t(a) * b) % mod;
}
int fpow(int a, int n, int r = 1) {
while (n) {
if (n % 2)
r = mult(r, a);
n /= 2;
a = mult(a, a);
}
return r;
}
const int max_n = 4.1e5;
int tree[4 * max_n];
int modif[4 * max_n];
int64_t pmask[4 * max_n], pushmask[4 * max_n];
vector<int> primes, revprimes;
void build(int v, int l, int r, vector<int>& a) {
modif[v] = 1;
if (l == r - 1) {
tree[v] = a[l];
for (int i = 0; i != SZ(primes); ++i)
if (a[l] % primes[i] == 0)
pmask[v] |= (int64_t(1) << int64_t(i));
} else {
int m = l + (r - l) / 2;
build(2 * v + 1, l, m, a);
build(2 * v + 2, m, r, a);
tree[v] = mult(tree[2 * v + 1], tree[2 * v + 2]);
pmask[v] = pmask[2 * v + 1] | pmask[2 * v + 2];
}
}
void push(int v, int vl, int vr) {
if (modif[v] != 1)
tree[v] = fpow(modif[v], vr - vl, tree[v]);
pmask[v] |= pushmask[v];
if (vl != vr - 1) {
modif[2 * v + 1] = mult(modif[2 * v + 1], modif[v]);
modif[2 * v + 2] = mult(modif[2 * v + 2], modif[v]);
pushmask[2 * v + 1] |= pushmask[v];
pushmask[2 * v + 2] |= pushmask[v];
}
modif[v] = 1;
pushmask[v] = 0;
}
pair<int, int64_t> get(int v, int vl, int vr, int l, int r) {
if (vr <= l or r <= vl)
return make_pair<int, int64_t>(1, 0);
push(v, vl, vr);
if (l <= vl and vr <= r)
return make_pair(tree[v], pmask[v]);
int vm = vl + (vr - vl) / 2;
auto r1 = get(2 * v + 1, vl, vm, l, r);
auto r2 = get(2 * v + 2, vm, vr, l, r);
return make_pair(mult(r1.first, r2.first), r1.second | r2.second);
}
void multiply(int v, int vl, int vr, int l, int r, int x, int64_t mask) {
if (vr <= l or r <= vl)
return;
push(v, vl, vr);
if (l <= vl and vr <= r) {
pushmask[v] = mask;
modif[v] = x;
return;
}
int vm = vl + (vr - vl) / 2;
multiply(2 * v + 1, vl, vm, l, r, x, mask);
multiply(2 * v + 2, vm, vr, l, r, x, mask);
pmask[v] = pmask[2 * v + 1] | pmask[2 * v + 2] | pushmask[2 * v + 1] | pushmask[2 * v + 2];
tree[v] = fpow(x, min(vr, r) - max(l, vl), tree[v]);
}
int main() {
std::iostream::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
// code here
for (int i = 2; i <= 300; ++i) {
bool ok = true;
for (int j = 2; j * j <= i and ok; ++j)
if (i % j == 0)
ok = false;
if (ok) {
primes.push_back(i);
revprimes.push_back(fpow(i, mod - 2));
}
}
int n = input<int>();
int q = input<int>();
vector<int> a(n);
input_seq(ALL(a));
build(0, 0, n, a);
for (int it = 0; it != q; ++it) {
if (input<string>() == "TOTIENT") {
int l = input<int>() - 1;
int r = input<int>() - 1;
pair<int, uint64_t> prod = get(0, 0, n, l, r + 1);
for (int i = 0; i != SZ(primes); ++i)
if (prod.second & (int64_t(1) << int64_t(i)))
prod.first = mult(mult(prod.first, primes[i] - 1), revprimes[i]);
cout << prod.first << "\n";
} else {
int l = input<int>() - 1;
int r = input<int>() - 1;
int x = input<int>();
int64_t msk = 0;
for (int i = 0; i != SZ(primes); ++i)
if (x % primes[i] == 0)
msk |= (int64_t(1) << int64_t(i));
multiply(0, 0, n, l, r + 1, x, msk);
}
}
return 0;
}
Submission link: 49740091
#pragma comment(linker, "/stack:247474112")
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int Mod = 1000000007;
int prime[] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137
,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293}; // (size = 62)
int modPow(int a, int b) {
int res = 1;
while (b > 0) {
if (b % 2 == 0) {a = (1LL * a * a) % Mod; b /= 2;}
else {res = (1LL * res * a) % Mod; b -= 1;}
}
return res;
}
struct ProTree {
vector<int> Tree, Lazy;
ProTree() {}
ProTree(int n) {Tree.resize(n*4, 1); Lazy.resize(n*4, 1);}
void Propagate(int node, int st, int en) {
if (Lazy[node] == 1) return;
Tree[node] = (1LL * Tree[node] * modPow(Lazy[node], (en - st + 1))) % Mod;
if (st != en) {
Lazy[node*2+1] = (1LL * Lazy[node*2+1] * Lazy[node]) % Mod;
Lazy[node*2+2] = (1LL * Lazy[node*2+2] * Lazy[node]) % Mod;
}
Lazy[node] = 1;
}
void Multiply(int node, int st, int en, int L, int R, int val) {
Propagate(node, st, en);
if (st > en || en < L || R < st) return;
if (L <= st && en <= R) {
Lazy[node] = (1LL * Lazy[node] * val) % Mod;
Propagate(node, st, en); return;
}
Multiply(node*2+1, st, (st+en)/2+0, L, R, val);
Multiply(node*2+2, (st+en)/2+1, en, L, R, val);
Tree[node] = (1LL * Tree[node*2+1] * Tree[node*2+2]) % Mod;
}
int Product(int node, int st, int en, int L, int R) {
Propagate(node, st, en);
if (st > en || en < L || R < st) return 1;
if (L <= st && en <= R) return Tree[node];
int p1 = Product(node*2+1, st, (st+en)/2+0, L, R);
int p2 = Product(node*2+2, (st+en)/2+1, en, L, R);
return ((1LL * p1 * p2) % Mod);
}
};
struct OrTree {
vector<long long> Tree, Lazy;
OrTree() {}
OrTree(int n) {Tree.resize(n*4); Lazy.resize(n*4);}
void Propagate(int node, int st, int en) {
if (Lazy[node] == 0) return;
Tree[node] |= Lazy[node];
if (st != en) {
Lazy[node*2+1] |= Lazy[node];
Lazy[node*2+2] |= Lazy[node];
}
Lazy[node] = 0;
}
void Update(int node, int st, int en, int L, int R, long long val) {
Propagate(node, st, en);
if (st > en || en < L || R < st) return;
if (L <= st && en <= R) {
Lazy[node] |= val;
Propagate(node, st, en); return;
}
Update(node*2+1, st, (st+en)/2+0, L, R, val);
Update(node*2+2, (st+en)/2+1, en, L, R, val);
Tree[node] = (Tree[node*2+1] | Tree[node*2+2]);
}
long long Or(int node, int st, int en, int L, int R) {
Propagate(node, st, en);
if (st > en || en < L || R < st) return 0;
if (L <= st && en <= R) return Tree[node];
long long p1 = Or(node*2+1, st, (st+en)/2+0, L, R);
long long p2 = Or(node*2+2, (st+en)/2+1, en, L, R);
return (p1 | p2);
}
};
int N, Q, l, r, x; string cmd;
vector<int> invPrime(62);
vector<int> A; ProTree PrTree; OrTree OSTree;
vector<long long> Mask(301, 0);
void PreprocessMask() {
for (int z=1; z<=300; z++) {
for (int i=0; i<62; i++) {
if (z % prime[i] != 0) continue;
Mask[z] |= (1LL << i);
}
}
}
void Input() {
for (int i=0; i<62; i++) invPrime[i] = modPow(prime[i], Mod-2); PreprocessMask();
cin >> N >> Q; A.resize(N); PrTree = ProTree(N); OSTree = OrTree(N);
for (int i=0; i<N; i++) {
cin >> A[i];
PrTree.Multiply(0, 0, N-1, i, i, A[i]);
OSTree.Update(0, 0, N-1, i, i, Mask[A[i]]);
}
}
void Solve() {
while (Q--) {
cin >> cmd >> l >> r; l--; r--;
if (cmd == "MULTIPLY") {
cin >> x;
PrTree.Multiply(0, 0, N-1, l, r, x);
OSTree.Update(0, 0, N-1, l, r, Mask[x]);
}
else if (cmd == "TOTIENT") {
int res = PrTree.Product(0, 0, N-1, l, r);
long long SegMask = OSTree.Or(0, 0, N-1, l, r);
for (int i=0; i<62; i++) {
if ((SegMask & (1LL << i)) == 0) continue;
res = (1LL * res * (prime[i] - 1)) % Mod;
res = (1LL * res * invPrime[i]) % Mod;
}
cout << res << endl;
}
}
}
int main(int argc, char* argv[]) {
ios_base::sync_with_stdio(0); cin.tie(NULL);
Input(); Solve(); return 0;
}
Submission link: 49739611
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize("unroll-loops")
#include <iostream>
#include <algorithm>
#include <vector>
#include <ctime>
#include <unordered_set>
#include <string>
#include <map>
#include <unordered_map>
#include <random>
#include <set>
#include <cassert>
#include <functional>
#include <iomanip>
#include <queue>
#include <numeric>
#include <bitset>
#include <iterator>
using namespace std;
const int N = 100001;
mt19937 gen(time(NULL));
#define forn(i, n) for (int i = 0; i < n; i++)
#define ford(i, n) for (int i = n - 1; i >= 0; i--)
#define debug(...) fprintf(stderr, __VA_ARGS__), fflush(stderr)
#define all(a) (a).begin(), (a).end()
#define pii pair<int, int>
#define mp make_pair
#define endl '\n'
#define vi vector<int>
typedef long long ll;
template<typename T = int>
inline T read() {
T val = 0, sign = 1; char ch;
for (ch = getchar(); ch < '0' || ch > '9'; ch = getchar())
if (ch == '-') sign = -1;
for (; ch >= '0' && ch <= '9'; ch = getchar())
val = val * 10 + ch - '0';
return sign * val;
}
const int mod = 1e9 + 7;
const int phi = 1e9 + 6;
const int M = 301, B = 500;
int P = 0;
inline int mul(int a, int b) {
return (a * 1LL * b) % mod;
}
int mpow(int u, int p) {
if (!p) return 1;
return mul(mpow(mul(u, u), p / 2), (p & 1) ? u : 1);
}
vector<int> primes;
vector<int> pi;
int pw[M];
int lg[N];
bool pr(int x) {
if (x <= 1) return false;
for (int i = 2; i * i <= x; i++)
if (x % i == 0)
return false;
return true;
}
void precalc() {
forn(i, M)
if (pr(i)) {
primes.push_back(i);
P++;
}
pi.resize(P);
forn(i, M) {
int x = 1;
forn(j, B) {
x = mul(x, i);
}
pw[i] = x;
}
forn(i, P)
pi[i] = mpow(primes[i], phi - 1);
}
struct product_tree {
vector<int> arr, block_product, block_update, single_update;
int n;
product_tree(vector<int>& a) : n(a.size()) {
arr = a;
while (n % B) {
n++, arr.push_back(1);
}
block_product.resize(n / B, 1);
block_update.resize(n / B, -1);
single_update.resize(n / B, -1);
for (int i = 0; i < n; i += B) {
int x = 1;
int pos = i / B;
forn(j, B)
x = mul(x, arr[i + j]);
block_product[pos] = x;
}
}
inline void add(int& u, int x, int mode) {
if (mode) {
if (u == -1)
u = x;
else
u = mul(u, x);
}
else {
if (u == -1)
u = pw[x];
else
u = mul(u, pw[x]);
}
}
void update(int pos, int x) {
add(block_update[pos], x, 0);
add(single_update[pos], x, 1);
}
void reconstruct(int pos) {
int e = single_update[pos];
if (e == -1) return;
int x = 1;
int l = pos * B, r = l + B;
for (int i = l; i < r; i++) {
arr[i] = mul(arr[i], e);
x = mul(x, arr[i]);
}
single_update[pos] = block_update[pos] = -1;
block_product[pos] = x;
}
void apply(int l, int r, int x) {
int L = l / B, R = r / B;
if (L == R) {
reconstruct(L);
for (int i = l; i <= r; i++) {
arr[i] = mul(arr[i], x);
block_product[L] = mul(block_product[L], x);
}
return;
}
reconstruct(L);
for (int i = l; i < (L + 1) * B; i++) {
arr[i] = mul(arr[i], x);
block_product[L] = mul(block_product[L], x);
}
reconstruct(R);
for (int i = R * B; i <= r; i++) {
arr[i] = mul(arr[i], x);
block_product[R] = mul(block_product[R], x);
}
for (int j = L + 1; j < R; j++)
update(j, x);
}
int get(int l, int r) {
int L = l / B, R = r / B;
int ans = 1;
if (L == R) {
reconstruct(L);
for (int i = l; i <= r; i++) {
ans = mul(ans, arr[i]);
}
return ans;
}
reconstruct(L);
for (int i = l; i < (L + 1) * B; i++) {
ans = mul(ans, arr[i]);
}
reconstruct(R);
for (int i = R * B; i <= r; i++) {
ans = mul(ans, arr[i]);
}
for (int j = L + 1; j < R; j++) {
ans = mul(ans, block_product[j]);
if (block_update[j] != -1)
ans = mul(ans, block_update[j]);
}
return ans;
}
};
struct prime_tree {
vector<ll> t, d;
int n;
prime_tree(vector<ll>& a) : n(a.size()) {
t.resize(4 * n);
d.resize(4 * n, -1);
build(1, 0, n, a);
}
ll build(int u, int l, int r, vector<ll>& a) {
if (l == r - 1) {
return t[u] = a[l];
}
int m = (l + r) / 2;
return t[u] = build(u << 1, l, m, a) | build(u << 1 | 1, m, r, a);
}
inline void add(ll& u, ll x) {
if (u == -1)
u = x;
else
u |= x;
}
void push(int u, int l, int r) {
if (d[u] == -1) return;
t[u] |= d[u];
if (r - l > 1) {
add(d[u << 1], d[u]);
add(d[u << 1 | 1], d[u]);
}
d[u] = -1;
}
void update(int u, int l, int r, int L, int R, ll x) {
push(u, l, r);
if (L >= R || l > L || r < R) return;
if (l == L && r == R) {
add(d[u], x);
push(u, l, r);
return;
}
int m = (l + r) / 2;
update(u << 1, l, m, L, min(m, R), x);
update(u << 1 | 1, m, r, max(L, m), R, x);
t[u] = t[u << 1] | t[u << 1 | 1];
}
ll get(int u, int l, int r, int L, int R) {
push(u, l, r);
if (L >= R || l > L || r < R) return 0;
if (l == L && r == R) {
return t[u];
}
int m = (l + r) / 2;
return get(u << 1, l, m, L, min(m, R)) | get(u << 1 | 1, m, r, max(L, m), R);
}
ll get(int l, int r) {
return get(1, 0, n, l, r + 1);
}
void apply(int l, int r, ll x) {
update(1, 0, n, l, r + 1, x);
}
};
ll transform(int x) {
ll mask = 0;
forn(i, P)
if (x % primes[i] == 0) {
mask |= (1LL << i);
}
return mask;
}
void solve() {
int n, q; cin >> n >> q;
vi a(n);
vector<ll> _a;
for (auto& v : a) {
cin >> v;
_a.push_back(transform(v));
}
auto Ptree = product_tree(a);
auto Mtree = prime_tree(_a);
int l, r, x;
forn(i, q) {
string s; cin >> s;
if (s == "MULTIPLY") {
cin >> l >> r >> x;
l--, r--;
Ptree.apply(l, r, x);
Mtree.apply(l, r, transform(x));
}
else {
cin >> l >> r;
l--, r--;
int product = Ptree.get(l, r);
ll mask = Mtree.get(l, r);
forn(j, 63)
if (mask >> j & 1) {
product = mul(product, primes[j] - 1);
product = mul(product, pi[j]);
}
cout << product << endl;
}
}
}
signed main() {
int t = 1;
ios_base::sync_with_stdio(0);
cin.tie(0);
precalc();
while (t--) {
clock_t z = clock();
solve();
debug("Total Time: %.3f\n", (double)(clock() - z) / CLOCKS_PER_SEC);
}
}











Thanks for FAST editorial :)
I believe the solution for the problem D is wrong. Take the following test case for example.
Its obvious the answer is supposed to be 2. But both the solutions give 3 as output.
Edit :- I misunderstood the question. There is nothing wrong.
yeah, test is wrong
Could you explain that for me? I don't know how to get 3 instead of 2.
Can you please explain how the answer is 3 and not 2
Starting index is 1 — 4 moves: [1 2 1 3 1] -> [2 2 1 3 1] -> [1 1 1 3 1] -> [3 3 3 3 1] -> [1 1 1 1 1] Starting index is 2 — 3 moves: [1 2 1 3 1] -> [1 1 1 3 1] -> [3 3 3 3 1] -> [1 1 1 1 1] Starting index is 3 — 3 moves: [1 2 1 3 1] -> [1 2 2 3 1] -> [1 3 3 3 1] -> [1 1 1 1 1] Starting index is 4 — 3 moves: [1 2 1 3 1] -> [1 2 1 1 1] -> [1 2 2 2 2] -> [1 1 1 1 1] Starting index is 5 — 4 moves: [1 2 1 3 1] -> [1 2 1 3 3] -> [1 2 1 1 1] -> [1 2 2 2 2] -> [1 1 1 1 1]
Can anyone elaborate how would we drop the third parameter if we compressed the array in the first solution of D?
Problem E. Yeah, probability to fail finding 30 random elements is small, yet random_shuffle() (to randomize a permutation) can't manage to be random enough. Is there an explanation for that? It's so strange
A nice post about this(and other things concerning randomness): https://codeforces.com/blog/entry/61587
You should read the header file in your compiler.
random_shuffle()usesrand(), and as a result, could fail as well along withrand()(though it took me a little more work to do so) :DAh... It's such a pity that I fail to submit my code of problem-F in the end. Just few seconds! I didn't think I should get a segment-tree template before, but now I realize it's really important especially for those people like me whose finger are frozen and type slowly.
Hmm...My fingers were also frozen,and so was my brain.I must have been crazy that I submitted the code to wrong problems twice
Looks familiar, don't you think so?
https://www.geeksforgeeks.org/largest-power-k-n-factorial-k-may-not-prime/
Hey?
https://math.stackexchange.com/questions/1087247/number-of-trailing-zeros-at-other-bases
https://www.quora.com/How-do-I-find-the-number-of-trailing-zeroes-of-N-factorial-in-Base-B
https://comeoncodeon.wordpress.com/2010/02/17/number-of-zeores-and-digits-in-n-factorial-in-base-b/
I can't read the codes for problems C and D!
Задача С
what would be the ans in test case in problem C:
5 100?
The number is (1, 20)100 so the answer is 0.
Since 20 has a trailing zero , shouldn't ans be 1?
Don't mix up 10-ary numbers and 100-ary numbers.
The answer would be 0. 5! is 120. 120 in base 100, would be (1)(20), where the 2 numbers in the brackets are the 2 digits in base 10. This is because 120 can be expressed as 1 * 1001 + 20 * 1000. Therefore there are no trailing zeroes.
How can we talk about changing the color of some squares in segment [l, r] if we don't know where our starting square is(Since the starting square is the only one whose component we may change)?
you need to make a for, leaving each Ci as initial, not to receive TLE, we need an array to save the previous results dp[i][j][1].
About B:
I had similar idea during contest, but didn't code it because i couldn't prove it. Still don't know its proof.
How to prove solution of B?
AkiLotus
Imagine the array where we remove all "irrelevant" elements that are not in the largest m * k elements. It is trivial to see that we can simply place the dividers for every m elements.
Then just re-insert all the "irrelevant" elements back into their proper locations and we now have our complete answer.
That is a very good way to imagine it. Thanks for sharing !
Could someone explain why this code is getting WA verdict at TC 10, 49727068 . It is the same approach as editorial and top users submissions.. I am unable to visualise the error.
You should divide tmp2 in such a case.
thank you so much.
Isn't the answer for D n-1-ceil(LPS/2) ?? ( of course in the compressed one (for example 112553 -compress-> 1253 ) )
n-ceil(LPS/2), yes.
But n-1-ceil(LPS/2) worked for the samples... :/
No, my bug can't be in my LPS.
Just dammit... I'm such a noob!!!
random_shuffle is deprecated
I'm sorry but, no.
For simplicity, assumed that the sequence a is [0, 1, 2, ..., n - 1]. Suppose that we randomly (and uniformly) select a subsequence S containing k elements from sequence a (when k is the number of ? query asked). Denote S = [s1, s2, ..., sk].
How exactly was I supposed to know that checker isn't adaptive? This isn't stated in statements, meaning that we can not just assume that we can query random elements. I've coded a solution, asking only
? iwhere i ≤ 30 just because non-adaptiveness wasn't stated in the problem statements. I'm almost sure at the moment that with adaptive checker this problem is basically unsolvable.What prevented you from asking?
Because this is common sense for interactive problems to explicitly specify whether checker isn't adaptive in case it being true. (if it is relevant to the solution)
I guess it's our mistake to not write it in statements, however we indeed answered this question in clarifications to all interested.
Also, I have a feeling that, at least on codeforces, we have an opposite situation: most of the interactive problems are not adaptive and when it is adaptive, it's written in statement (basically, since there is a need to specify hack format, it's mentioned, that jury can play differently).
I think in most cases it's better not to write anything about interactor. Participants should be prepared for the worst case.
Worst case is that jury's own randomised solution also fails in adaptive interactions!
smh problem A was obviously max flow, how did this contest even get accepted!? 49718487 :D
I try to say something more funny about this but i cant
R.I.P
If you are a RED CODER and contest is unrated for you that is how you approach easy implementation questions.
Next time I should invite millions of friends for our grape party.
Can someone help with problem C. I am getting a WA on pretest 10. 49731384
Seems like an overflow issue
ff = ff * i.ff;What would happen if i.ff is something around 1e10 or so?
Got it. Thanks. Correct submission 49736095.
But won't this check for the overflow? I mean, if
ff = ff * i.ffoverflows wouldn'tffgo less than 0?It is not "Guaranteed" to go less than zero. It actually may give you some value in long long range, with some behavior similar to modular arithmetic (though instead of 0~MAXIMUM, it can give you -2^63 to 2^63-1). It depends on what i.ff was.
Oh! Thanks,
https://codeforces.com/blog/entry/65033?#comment-491516 https://codeforces.com/blog/entry/65136?#comment-491458
Seems like there are a bunch of codes with same issues.
Yeah. A lot of my friends got wrong answers on Pretest 7 and 10. if
long longis changed tounsigned long longpretest 7 will pass.How to prove B ?
You have to choose m * k max. Let's write them somewhere, and if you have a segment from l to r and there are any m maxima in it that you wrote out, then the segment can be finished, so you will have m maxima in the first (k — 1) segment from those that you wrote out. And you will have a segment of length greater than or equal to m, since you have not chosen the remaining m peaks.
Take k=2 and think about it, I guess everything will be clear then
You just take M*K largest numbers. Obviously if we can use them for constructing subarrays they will provide the best result. Let's sort them by positions in the list. take the first M numbers and call their union "the 1st subarray", then the next M numbers, call them "the 2nd subarray" and so on. We constructed K subarrays which give the best result for this problem. There is nothing contradictory in this construction, each subarray has at least M elements and there are no upper bounds on the sizes of subarrays. So they're valid and this solution works.
Prob E:
I've got WA on first 2 submission 49735490, 49734969
Then after some minor changes I've got AC 49736359. I guess that even with little probability, it could still f- you up after all :<
Still, congratz on successfully held such an amazing contest like this on codeforces ^^ Hope to see more from us vietnamese and maybe more from HNA alumni if possible <3
Thanks. ;)
Just realized, I haven't worked with HNA's Informatics Team ever before.
Maybe in the near future. ;)
Well that day could be nearer than you think ;)
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
i love fast editorials <3
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
For D, I use the same dp state, dp[l][r][0/1]. But I get wa on 8 :( This is my code: https://codeforces.com/contest/1114/submission/49737924
For F problem we should precompute inverses of primes <300 ( mod 10^9+7) and then use it to multiply our answer by (p-1)/p, am i right?
I am not getting the cause of difference between the output of the same code when submitted on codeforces and on ideone..?
@Akikaze @GreenGrape Can anyone tell why this solution is getting WA verdict? Offline it gives correct output for same test case and on other online compilers(ideone) also it works fine. Why it does not work on Codeforces?
Can't understand the second solution for problem D.
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
Thanks. First D solution was helpful to me. How intuitive and pretty it is!
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
1114B I can't understand (division[i] = ind[(i+1)*m — 1];) of M.xuanquang1999 solution....any explanation ?
indstore the indices of m * k largest elements in the array a, sorted in increasing order. This array is 0-indexed.division[i]store the ending indices of the i-th array. This array is also 0-indexed.Since we need m elements for each subarray,
division[i]is the value of the (i + 1) * m elements in ind. So,division[i] = ind[(i+1)*m - 1](-1 becauseindis 0-indexed).Thanks..I got it
Please cdkrot, may you explain to me the following cases in the first solution of D:
For dp[l][r][0], dose your code take in consideration dp[l][r - 1][0] and dp[l][r - 1][1]?
I see that your code, for calculating d[l][r][0] takes in consideration just dp[l + 1][r][0] and dp[l + 1][r][1]!
And also this is hold for dp[l][r][1] where I see that your code doesn't take in cosideration dp[l + 1][r][0] and dp[l + 1][r][1]!
And when I took those states in consideration, my submission failed on test 8, where my answer is smaller than judg's answer. So, please where is the wrong?
UPD: now I know why my submission was wrong, and corrected it. But still don't know the proof behind those states being negligible!
hi~ would you like to explain why it is wrong? I have the same problem with you. I keep on getting WA on pretest 8.
Hi,
while calculating dp[l][r][0] and taking dp[l][r - 1][0] in consediration, we shouldn't add just 1 if a[l]! = a[r], we should add 2, because we need one turn to flood all the segment [l, r] with color a[r], then another turn to flood this segment with color a[l] (because that is what we are calculating).
Why we should flood the segment with color a[r] firstly? why not just flood it with a[l]?
The answer: the start point of all process should be still in segment [l, r - 1] to not clash with the fact that we cannot change the starting point.
And this case is the same while calculating dp[l][r][1] taking in consediration dp[l + 1][r][1].
The states are simple: note that in every moment the component containing a starting cell forms a segment and has its color equal to one of the ends of this segment.
And then there are few transitions between
Can you explain why it is unnecessary to consider dp[l][r - 1][0] and dp[l][r - 1][1] for calculating dp[l][r][0], please? Just because they need more transition?
Note, that I've written in "forward dp"-style, that is, I update the next states using the current one.
And if the current state is [l;r] and some color c, then extending to [l - 1;r] will make the segment having color[l - 1].
And we can add the transition to [l - 1;r], color[r], by saying "go to state [l - 1, r], color[l - 1] first and then recolor again.
But this is not necessary: there is no need to recolor to stay in the same segment, it's easy to see that it's not optimal (formally, not better than not doing this) ;)
Thank you!!! I can understand it now.
I also tried to prove dp[l][r][0] + 2 ≥ dp[l][r][1] + 1, which comes from dp[l - 1][r][0] = dp[l][r][0] + [s[l - 1] ≠ s[l]] + [s[l - 1] ≠ s[r]] and dp[l - 1][r][1] = dp[l][r][0] + [s[l - 1] ≠ s[l]].
I guess |dp[l][r][0] - dp[l][r][1]| ≤ 1 is always true, and this submission(49850235) shows it is always true. But I don't know how to prove this.
With dp[l][r][0] + 2 ≥ dp[l][r][1] + 1, it means two transitions are always worse than those with one transition, so dp[l][r - 1][0 / 1] needs two transitions to reach dp[l][r][0] and therefore is worse than dp[l + 1][r][0 / 1].
This is not intuitive :( I think your explanation is better!! :D
|dp[l][r][0] - dp[l][r][1]| <= 1 is always true.
Suppose we can color [l,r] with color c_l in x steps. Then we can color [l,r] with c_r in x + 1 steps by first coloring to c_l in x steps then 1 more step to change color to c_r. Therefore the larger one is at most 1 more step than the smaller one.
My solution to problem F has complexity N*log(N) + Q*(log(N)+P) where P = 62 is the number of primes. Here's what I did : We need basically the product of values in the range l to r and for each prime, we need to check whether that prime exist in the range l to r. Product of values can be done in log(N) using segtree or bit. Now I created another segtree where each node has a bitset, which tells whether ith prime occured or not in the range. So we just have to do OR of all the bitsets. So operations on bitset is now almost O(1) (more precisely O(P/32)). But still my soln got tle due to heavy modulo operations. To reduce the number of modulo operations, I took the discrete log of all the values. Now the problem changes to range addition and range sum. The solution is very fast after taking discrete logarithm. Here's my submission : 49740935
You can use long long instead of bitset<62>.
How did you choose the base of the discrete log? Just some brute force?
You find a primitive root in O(sqrt(MOD) * log(MOD)) or faster (or bruteforce and copy+paste it). Any primitive root is good enough.
The method that I understood from Wikipedia page is
But I can't see why this is O(sqrt(MOD) * log(MOD)). It looks like O(sqrt(MOD) + log^2(MOD)*R) where R is the root.
That's kind of the method that I was talking about. The specific details of implementation change the complexity of the second check (in some code, people actually do O(sqrt) loop to look through every divisor of phi(n)).
As for why I ignored R, R will be very low. The are phi(phi(N)) primitive roots of N. This number is really large and if you calculate the probability that a random number is a primitive root it's large enough that with a few tries it'll find one.
Thanks for sharing — nice trick!
For your initial solution, do you have an implementation which will be N*log(N)? As far as I can tell, it has additional log(N) factor because you need to do exponentiation to apply "multiply on a segment" update — for example, in
line in your code (49718093) — so it is not just "heavy modulo operations". For a few minutes I tried to find some workaround to shave off that log(N), but I didn't succeed.
Hmmm. You are right. The soln was getting tle because of the additional log(N) factor because of exponentiation and the previous soln was not N*log(N), rather N*log^2(N). But since the editorial soln has a complexity of log^2(N), I believe the solution got tle because of heavy modulo operation. I also couldn't remove the log(N) factor by any means. Thanks for noticing it!
For D how do we prove that when we are flooding [L, R], minimum would be when we either color it with cL or cR. Why not with anything in between?
In a turn, you always change the color of the connected component containing the starting square. So you have to change it to the color of the left or right component to be able to "merge" them.
Makes sense, thanks!
how to solve if starting square is not fixed?
can anybody confirm that 49761228 will be the solution for above case.
If it's possible to change the color of any component in a turn then it becomes problem K from 2008 Moscow Subregional. I don't know any solution better than O(n^3) for this problem.
Your code gets WA in case
The answer is 10.
Ohh, thanks a lot.
Because of the start point being unchangable, so, wherever you start the process, the first time the interval will be flooded with the same color, this color will be one of the two ends' color.
So, if the minimum number of turns for reaching the same color the first time is x, any other turns to any other color will be added to x making the answer bigger.
I meant Say we have 1 2 2 3 Then we can also change it optimally to 2 2 2 2 ( 2 moves ) But it will never be better than changing to L or R. Can be equal though.
Edit: this state can't be reached
It's not possible to achieve [2, 2, 2, 2] from [1, 2, 2, 3].
Ok, I reread the question and realized it now :(
Thanks both of you for your help!
With 2 moves, I think, but it's possible in 3 moves:
By selecting index 1 as starting index (1-indexed):
[1, 2, 2, 3] -> [2, 2, 2, 3] -> [3, 3, 3, 3] -> [2, 2, 2, 2].
I am still finding it difficult to understand the problem statement.
[1, 2, 2, 3] -> [2, 2, 2, 3] -> [2,2,2,2]
In above case, the connected component of 3 is just 3 itself and the starting connected component is at position 4(1-based indexing) and then we change this starting component to 2.
Kindly help in my wrong undertanding.
In the first step, you decided that the starting point of the process is position 1 (1-based indexed), and according to the problem's statement, one cannot change this position along the whole process, so you cannot change it to position 4 in the next step.
So, that means if I select index 2 as the starting position then
[1,2,2,3] -> [1,3,3,3]
So, after this, I won't be able to change the configuration further because this is the last configuration. Right?
[1, 2, 2, 3] - »» [1, 3, 3, 3] - »» [1, 1, 1, 1] - »» [2, 2, 2, 2] - »» and so on...
So, you can always change the segment that the starting point lies in.
Aah Sorry my mistake
Thanx brother
Not bad. Welcome brother!
KEK
LOL
Can somebody explain the idea and logic behind Problem B using Nth_element concept as mentioned in editorial
problem C is just WoW! learned so many things! Thank you for such a beautiful problem <3
Yeah, but indeed it is a bit straightforward if you know this: https://en.wikipedia.org/wiki/Legendre%27s_formula But still a good one for Problem C!
pE : doing binary search on rank of an element requires only log( n ) = 20 queries
xuanquang1999, What does od{x} represent in the proof of problem E?
It is a formating error. What I supposed to write is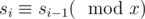 .
.
Yeah, I didn't see that formatting error at first. It's now fixed. ;)
Who can tell me about problem A that why there are '>=' in the tutorial but '>' in the solution?
Well never mind, it's my mistake = =
in problem D, i found a lot of accepted solution (tutorial's solution included) that give the answer of 5 for the test :8 5 2 6 2 4 3 4 5. However I think the correst answer is 4. Can anyone explain this for me?
hi~ in the problem statement, you need to change the component containing the start one to any other color every turn. I think you want to change 6 first and then 3. But this operation is forbidden.
May I ask you a question? if each turn we can choose a connected block arbitrarily,then how to solve the problem?
oh my mistake. Thank you
In problem F we have several ways to maintain the segment products with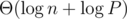 per query/modification. Here is my approach: Suppose we have 2 structure T1 and T2 which can maintain the prefix product and allows us to modify one place of the array with
per query/modification. Here is my approach: Suppose we have 2 structure T1 and T2 which can maintain the prefix product and allows us to modify one place of the array with 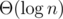 (Obviously both segment tree and fenwick tree can do it.) We will just discuss about how to handle the modification with r = n and the query with l = 1 (Other modification could be splitted into twice this kind of modification). Then the contribution of a modification on position l for a query on position r (l ≤ r) will be xr - l + 1 = xr / xl - 1. So we can maintain
(Obviously both segment tree and fenwick tree can do it.) We will just discuss about how to handle the modification with r = n and the query with l = 1 (Other modification could be splitted into twice this kind of modification). Then the contribution of a modification on position l for a query on position r (l ≤ r) will be xr - l + 1 = xr / xl - 1. So we can maintain 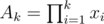 with T1 and
with T1 and 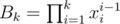 with T2. Then Arr / Br will be the result of
with T2. Then Arr / Br will be the result of
query(r). Here is my implementation with fenwick tree.Another way is to maintain the discrete logarithm of the product, then the multiplication will be converted to addition modulo P - 1. But we need to calculate the discrete logarithm of 1, 2, ..., 300.
Nice approach. Thanks!
Can anyone explain the approach to calculate xi in C? Thanks a lot!
This can be done using Legendre's formula. You can read more about it here: https://en.wikipedia.org/wiki/Legendre%27s_formula
I got it. Thx. :)
Can someone please help me in my C problem
49735519
number
bcan be prime. Andb * bcan be> long long MAX.now=pow(k,i)in functioncalciis wrongThanks a lot !
For D it says "To find the longest palindrome subsequence, we can make a reversed copy of the array and find LCS of it with the original array."
Sometimes strings will have multiple LCS's: some are palindromes and some are not. (For example the string "CABCA" and its reverse "ACBAC" have "ACA" as a palindromic LCS and "ABC" as a non-palindromic LCS).
How does one modify the LCS algorithm to always return a palindrome?
For every non-palindrome LCS, its reverse is also a LCS. In your case, CBA is also a valid LCS. Then you can just find half of any LCS then mirror it.
I'll put a link because it's faster than explaining. It even uses your example (lul).
In fact you can use an average LCS tracing without modification. Just make sure you go the topmost or bottommost route in the DP table. You'll end up with some arbitrary LCS if you choose some random valid trace path.
Why does tracing the topmost or bottommost path in the DP table yield the palindrome LCS?
xuanquang1999 I can't understand why .
.
Let D(S) the GCD of all difference between consecutive elements in S = {s1, s2, ..., sk}. In other word,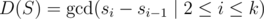 .
.
Then:
You should check out the article about Mobius inversion in the editorial (especially the first example in the article) to understand this better.
Oh, I didn't notice that I should turn the formula into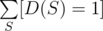 . Thanks a lot!
. Thanks a lot!
If the rest of problem D remains unchanged, and each operation can choose a connected block arbitrarily to change its color,then how to solve the problem?
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
For D: "Alternatively, we can also use the first solution on the compressed array, without needing the third parameter."
Can someone explain how to do it without the third parameter?
After compressing, let dp(l, r) be the minimum number of moves needed to make interval [l, r] into a single component. The answer is just dp(1, m), where m is the size of the compressed array. The base case is dp(x, x) = 0 for each x,
The key here is that after turning interval [l, r] into a single component, all the interval will always have the same color as either element l or r had initially. This gives the transition dp(l, r) = min(1 + dp(l + 1, r), 1 + dp(l, r - 1)), the former if our final step is including the l-th element into our component and the latter if it's including r. (By the observation one of those is always the last step). The exception is the case where the elements l and r are equal, in which case the answer is 1 + dp(l + 1, r - 1), because we only need one move to include both l and r into our component.
hi can you please explain how monochromising the segment to its ending colors always take minimum operation,and how you got this DP recurrence idea ,my second question is bit stupid but i would be very thankful if you could answer that also.
49765798 Can someone tell me why is the memory limit exceeded? (Problem D)
Overflow issues.The value of j might exceed maxn.
Because
#define int long long.Thanks!! This was indeed the problem. But why does it lead to MLE?
Long long uses twice the amount of memory int does. Your solution with ints used ~190MB and memory limit is 256MB.
You can use sizeof(int) and sizeof(long long) on your pc or in custom invocation to check this.
My submisstion using rand() passed just fine... I've yet to see one where I have to use mt19937 generator instead of normal one... 49774343
I've expected this solution and didn't intend to kill it.
Imagine a sequence from 0 to 106 - 1, its mean and median will be both 500000, and the standard deviation would be 288675.
Now, imagine a list of 107 random integers generated by your algorithm. A source code might be as of following:
And the output:
Pretty close to the perfect distribution.
I loved problem B and D
B is a tricky problem.
Can you explain this line Suppose squares [L, R] are flooded, then they are either of color cL or cR I m not getting it
say , [L,R] flooded , no matter with which color....ok?
if we take L-1 then new segment [L-1,R] will be flooded with the color[L-1]
else we take R+1 then new segment [L,R+1] will be flooded with the color[R+1]
so , no matter which one is our new segment ([L-1,R] or [L,R+1]) we always can say that our new segment [l,r] is flooded with the color[l] or color[r]
Can you please explain me, why this works on Python, but not on PyPy.
49779398 49779361
Literal String Formatting was added in Python version 3.6.
Since Codeforces uses PyPy3.5 v6.0 you get a SyntaxError on line 48 and 70.
I must say that as a new programmer, the way you're written problem A and B is so clean and nice and I love it.
Most other programmers use complicated code that I feel like sometimes is there for no other reason than to show off.. I have no problem with complicated code as long as it gets explained, the weird thing is that even tutorials use complicated code that doesn't get explained..
I haven't tried other problems but I will try to do them by myself.
I still think that this E is wrong .-.
In the 1st editorial of problem D why are we always making L-R as either CL or CR can't we change the color to some other color in that Range such that the cost of operations will become minimum.
Hello, I have a question on problem F.
This submission is getting MLE. I think I can reduce the memory with state reduction(
node.cumulfactorsis removable if I change the logic a bit) but it still requires at least 200MB. My original submission is using almost 500MB while some other participants are passing this problem with less than 50MB of memory usage.Let me say the main question. The bitmasking(to reduce memory) is mentioned on tutorial and I studied but I still cannot understand how bitmasked information can contain number of prime divisors applied so far. I think bitmasking can store only the information about the used prime divisors, not total number of each used divisors.
Can anyone explain? Thank you.
You don't need the quantity of each prime factor.
You can read the formula again, the Euler totient of the range product is in fact the range product itself, multiplied by for each distinct prime factor p appearing on the range product.
for each distinct prime factor p appearing on the range product.
How can I multiply into result since the result is represented in mod 109 + 7?
into result since the result is represented in mod 109 + 7?
Multiply the sum product by p - 1 first. then multiply the result by the modular inverse modulo 109 + 7 of p.
Since the constraints guaranteed , the modular inverse of p is simply pφ(mod) - 1, or p109 + 5, modulo 109 + 7.
, the modular inverse of p is simply pφ(mod) - 1, or p109 + 5, modulo 109 + 7.
Oh my god, extending Euler theorem lead the way to prove! Thank you!
Imho, two problems from this contest for me seems very similar to these one: Similar to problem C, oh not similar, they are actually equal, just different constraints, but solution is the same. Similar to problem F, not so similar, but if you know solution to this one, you will easily solve F.
The problem similar to F looks familiar — I found it on one Vietnamese National ICPC and take the core idea from this. However, later on thanks to cdkrot's suggestions, I increased the constraints and get rid of the multiple segment trees approach. Without that straightforward solution, it'll be quite tricky and require sufficient math backgrounds to surpass.
About C, I have seen many others pointing the same thing. Honestly, I haven't heard of any of those references, and none of my partners told me as well. ;)
Could you please elaborate on how to solve the second task?
Calculate the exponential of each prime in a seperate segment tree.
And how to do queries 0?
Why does it say in the statement that P ≤ 109 and in example it's P = 109 + 7?
As X <= 100, there are 25 primes up to 100. Store 25 seg trees for each prime, i-th denotes exponential of i-th prime in segment l_r. So when comes query multiply x, we just factorize x and add in segment l_r to every prime that took place in factorization. Division is the same, now we just do not add, we subtract. Calculating answer is to bruteforce all 25 primes and calculate product of primes powered to the sum of its segment tree in l_r.
Nice (:
I thought that involving fast power would lead to TLE due to that log factor, but i tried and it passed in 800ms. Thanks anyway.
Why my code for F has different results on codeforces and my PC?....please
https://codeforces.com/contest/1114/submission/49812712 on my PC,the results is right , but when I submit my code the output is weird... thx
better code for understanding problem D https://codeforces.com/contest/1114/submission/49815297
Problem A:My submissions were not passed until I had submited six times,I am so sad!
can someone explain what do we have to do in second part of second question??pleaseee
Have a look to this comment — https://codeforces.com/blog/entry/65136?#comment-491791 After you have found m*k elements sum, all you need to do is traverse original array again(unsorted/input array) and print out index+1(or index if 1-indexed base arr.) if you found m elements — This step has to be done k-1 times.
Auto comment: topic has been updated by AkiLotus (previous revision, new revision, compare).
Hey neko_nyaaaaaaaaaaaaaaaaa.
Can you please elaborate your solution of question D and explain the reason behind finding the longest palindromic subsequence and also the reason behind the following line of code:
cout << n — (dp[n][n] + 1)/2 << '\n';
Thanks in advance!
Try solving this problem: given a starting square, find the fewest number of turns possible.
Example:
The answer is 4 turns.
Consider the subarrays expanding to the left and right sides of the starting square. In this case left side = 2 5 4, right side = 3 5 4. The number of moves you need is |L| + |R| - LCS(L, R)
You want to find the maximum LCS across all starting squares. This gives an O(N3) solution.
Notice that "LCS expanding from a center" is simply a palindrome subsequence. You want the longest LCS, so you can simply find the longest palindrome. Now you have an O(N2) solution
neko_nyaaaaaaaaaaaaaaaaa I do not have a problem finding the long palindromic subsequence but can you please tell that why are we actually finding it and also why after finding it
|L| + |R| - LCS(L, R)
is providing us the answer.
Problem C:
r=min(floor(xi/yi)) where i=1 to m
Why does it work?
any proof?
Basically you are checking if given set of prime frequencies of 'b' exists in the same prime set frequencies of n. If "yes" increase result by 1, and decrease all the frequencies of prime factors of n by the corresponding freq. of b prime factors. Repeat the process, until you dont found such, then return result. This is similar to finding min(floor(xi/yi)) where i=1 to m.
Idea is basically to check if (n!%b == 0) repeatedly (by doing n!/=b), so we just check prime factors of b and their frequencies in prime factorization of n!.
my solution on F is exactly same with the Tutorial but i get TLE,what's the problem of my code ?
Problem F , Is it many time-complexity difference recursive power function and bottom-up power function? First, I used recursive power function. but got TLE. so, i saw another people's codes, they used bottom-up power function. i fixed my power function, and i got accepted.
TLE : https://codeforces.com/contest/1114/submission/49850747
ACCEPTED : https://codeforces.com/contest/1114/submission/49852069
In fact recursive function is somewhat (significant enough) slower than normal function. You can compare between 49740091 {non-recursive} and 49863959 {recursive}.
Still, the calculations can be quite faster if all integers are stored in
intand casted intolongonly before multiplication.Can someone tell the explanation of first proposition in Problem C?
Let say that x=n! is some number with zeroes in the end.
Trim all those zeroes and call new number y.
Then, x = y*(b^r), — here b and r is from editorial and r is number of zeroes in the end, because b^r is 1 and r zeroes in the end similarly to decimal numbers.
Fundamental theorem of arithmetic says that there is unique factorization of any number.
Thus, x has b^r in factorization.
in F problem you have missing powers for primes in place where you proving that answer is n*product.
Can you please specify the error location?
sorry, I'm wrong. I thought ai are primes, thus, they should have powers. but in text it's values from array.
In the tutorial of Problem C: Initially, denote xi = 0. **** Repeatedly do the following: add to xi, then divide n by pi. The loop ends when n is zero. When i want to find each xi,why do this?
In n! exactly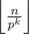 numbers are divisible by pk but some of them are also divisible by pk + 1 and so on. If you consider how many times you will count numbers that is divisible exactly by pk you'll see that they are included in all
numbers are divisible by pk but some of them are also divisible by pk + 1 and so on. If you consider how many times you will count numbers that is divisible exactly by pk you'll see that they are included in all 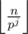 with j up to k. So, you'll count p exactly k times for this numbers. And using property that floor(n/p^k) = floor(floor(n/p)/p) you get repeated division by p.
with j up to k. So, you'll count p exactly k times for this numbers. And using property that floor(n/p^k) = floor(floor(n/p)/p) you get repeated division by p.
in problem B, how to find partions??
consider largest m*k numbers. mark them with 1 in some additional array. pick first m numbers and assign them to first segment. pick second m numbers and assign them to second segment. and so on. you'll get exactly k segments — obviously. none of segments can be smaller than m, because they all of them contain at least m numbers. all you need to do now is to cover gaps. you can do that by joining gaps to any segment nearby. other easier way to make partitions: just make cut each time when you reach m numbers in segment, and then reset counter of numbers you picking (marked ones) to zero.
Getting a strange compilation error("Compiled file is too large [53650389 bytes], but maximal allowed size is 33554432 bytes") in problem F. How to overcome it ?? My code https://ideone.com/5ijuXg
This was a really great contest by talented authors ! I learnt a lot solving problems of this contest.
I actually found the B more challenging than the C.
D was a very nice DP. I noticed the editorial used a 'forward-dp'. I tried understanding the transition and writing a 'backward-dp' so that I can understand it wel E was a good interactive problem.
F was a really good question. First, noticing that you do not need to know the exponent of each prime in the product, just their list. And then maintaining a product segment tree and a bitmask OR tree. Amazing !
Here are my solutions :)
Hello. I have a question about problem D
I made a testcase below
5
5 6 5 7 5
I think the answer is 2 ( [5 6 5 7 5] -> [5 5 5 7 5] -> [5 5 5 5 5] )
but, the output of both solution is 3.
Please anybody correct me
All transformation must include one cell being chosen as the starting cell.
Oh. I miss that condition.
Thank you!
Can I have one more question??
I just read problem D one more time.
But, I don't understand well
My question is here
In testcase [5 6 5 6 5], output is 2
In testcase [5 6 5 7 5], output is 3
What difference??
Like you might guess, the optimal solution starts with choosing the 3rd cell as the initial cell.
Then the process goes as following:
Again, we can still choose the 3rd cell as the initial cell.
Then the process goes as following:
Keep in mind that, each time you change the color of the initial cell, you change the color of all reachable cells having the same color as it as well.
Thank you!
I appreciate your kind explanation
AkiLotus you wrote in problem E's editorial: d will be calculated as greatest common divisors of all difference between all consecutive elements, provided all elements found (yes, including the max one) is kept into a list sorted by increasing order. Won't the probability of success be higher if we obtain the numbers and rather than taking the gcd of only the difference of consecutive elements take the gcd of absolute difference between all pairs of them ?
Both approaches literally yield the same value. This is due to the nature of Euclidean algorithm in finding GCD.
Can you provide any proof or references maybe ? I was thinking for some case like when the elements are a+d, a+2d, a+5d, taking adjacent elements' difference will yield d and 3d only whereas taking all pairs will yield d, 3d and 4d. I know the elements in the second list will be linear combinations of elements in the first list. So, is that somehow the reason that they don't add much value or what ?
You can refer to the Euclidean algorithm here.
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number.
Thus, the linear combinations of a set of number yield the same GCD as that set alone.
Thanks.
the problem C gives correct answer in geeks-ide (link is given below) for the 7th test case but wrong answer in codeforces not sure why::
https://ide.geeksforgeeks.org/NY6e3NArcO
https://codeforces.com/contest/1114/submission/50059493
7th test case input : 1000000000000000000 97
expected output: 10416666666666661 (i am getting this in geeks ide)
wrong output in codeforces: 10416666666666639 (not sure why )
This is one of the tests specifically designed to counter solutions with poor overflow handle.
Take a look at this part of your code:
mulmight even breach the limit of int64.In problem C, i have found some incorrectly index from editorial:
The process of finding p1, p2, ..., pn, y1, y2, ..., ym can be done by normal prime factorization of the value b.
the pi is the prime factor of b. So, the last boundary index. it's should be pm not pn.
however, it's not importance more. if you have understood in idea.
Thanks for noticing, it's fixed now. ;)
Please help me in understanding question D. Testcase: 8 4 5 2 2 1 3 5 5
Why is the answer for this 4? I think it should be 5. Where am I wrong? My procedure if I take starting square as 5: 4 5 2 2 1 3 5 5 4 2 2 2 1 3 5 5 //Step 1, 4 4 4 4 1 3 5 5 //Step 2, 1 1 1 1 1 3 5 5 //Step 3, 3 3 3 3 3 3 5 5 //Step 4, 5 5 5 5 5 5 5 5 //Step 5,
I didn't understand the explanation they gave in the question. Explanation: In the second example, a possible way to achieve an optimal answer is to pick square with index 5 as the starting square and then perform recoloring into colors 2,3,5,4 in that order.
You're taking the 2nd element (with color 5), not the 5th element.
The most optimal way is as following:
Oh thanks I got it. I thought we have to stick to a connected component but seems like we can switch between them.
No, we still have to stick into one connected component. As you can see all segments I performed color change included the 5th element (yet with different color).
For problem 'D', the claim, "Suppose squares [L, R] are flooded, then they are either of color cL or cR", I've been trying for some time to prove this claim using Mathematical Induction, but I'm unable to do it, and although it seems somewhat intuitive, it'd be great if someone can provide a proof for it. Thanks! cdkrot neko_nyaaaaaaaaaaaaaaaaa
The claim is pretty much self-explanatory.
If [L, R] is already connected at the initial state, then the claim is obviously true.
Let's denote the starting cell's index as i (L ≤ i ≤ R).
If [L, R] are flooded, then before the last flooding there exists two components [L, x] and [x + 1, R] (L ≤ x < R). Consider the two cases:
Sorry, I couldn't understand the proof properly. "Let's denote the starting cell's index as i", What is starting cell here?
Also, suppose the segment contained within [L, R] is: 1 2 2 3 3 3 4. Here we can do: 1 2 2 3 3 3 4 ---> 1 3 3 3 3 3 4 ---> 3 3 3 3 3 3 4 ---> 3 3 3 3 3 3 3, which is also optimal, and the resulting color is not 1 or 4.
If this segment contained within [L, R] was surrounded with lots of 3's on either side, then shouldn't we solve [L, R] this way, where we do not flood [L, R] with neither CL or CR? Or am I completely missing out on some point here?
Yes, you are missing out on some point. Please read the problem statement carefully.
The statement clearly says pick any square at the start of the game. Then you can only change the component containing that square. Thus, your 3rd move is not valid.
I see a lot of people have trouble with this. Maybe I should've highlighted something. I apologize for this.
Sorry, my bad.
Thanks for explaining! :)
Soln got accepted when i did 2 changes in tutorial's soln 1. I think we don't need to include Max in List, after sorting bcoz rest of the element would decide the value of d soln without including -- got accepeted 2. We only need series from 0 to +1000000000 bcoz numbers in AP can be possible from 0 to +100... not from -100... to 100... it got accepted using series from 0 to 100... correct me, if i'm wrong -- it would help me & other understanding the concept more better
Yeah, you can exclude Max from that part. The probability to get incorrect answer would be increased a little bit, but still insignificant to cause an issue for normal upsolving. ;)
For those not getting mistake in Div2 D, try this testcase- 7 4 3 4 2 5 3 5 answer should be 3 upvote if you r getting 5
can someone explain recurrence relation for first solution for prob D ?
ok