mohamedeltair's blog

Guaranteeing valid chosen segments in (Zero XOR Subset)-less problem?
By mohamedeltair, history, 5 years ago, In English

The question is about this problem: (Zero XOR Subset)-less.

The problem's editorial describes the solution as follows:

First let 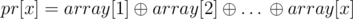. If we divided the array into k segments, where the right boundaries of these segments are (in increasing order) i1, i2, …, ik (ik must be n), Every segments subset-xor can be represented as pr[ij] subset-xor. Therefore besides maximizing k, we want to guarantee that the any pr[ij] non-empty subset has a non-zero XOR-sum. So we calculate the basis size of pr[1], pr[2], …, pr[n] numbers (binary vectors) under GF(2). Because the basis size will represent the maximum k such that all pr[ij] are linearly independent under GF(2) (no pr[ij] non-empty subset has a zero XOR-sum).

My question is: from the calculated basis size k, we know that we can choose k linearly independent (under GF(2)) pr[ij] values, but how do we guarantee that we can choose these values such that ik = n (as the last right boundary of our chosen segments has to be n)?

Thanks in advance.

  • Vote: I like it
  • +4
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it +5 Vote: I do not like it

If prn = 0 it's clear that answer does not exist (because XOR of all segments will be always 0 despite of partitioning).

Otherwise if prn is not in maximal basis let's look at basis decomposition of prn (it always exists, because otherwise it's possible to add prn to basis and basis is not maximal), remove any decomposition element from basis and add prn. Resulting set of vectors obviously has the same size as maximal basis and vectors in it are linear independent (let xi be elements in basis decomposition of prn, then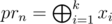 , so each non-trivial zero linear combination of vectors in new set of vectors leads to non-trivial zero linear combination of vectors in old set, which is impossible).

However, this fact wasn't required to solve this problem, you can simply add prn to basis at first stage of Gaussian elimination and basis will always contain prn (moreover, it is another proof of this fact because all bases of set of vectors have the same size).

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    So this means: for a set of vectors V with maximal basis of size k, if a non-zero vector v belongs to V, we can always construct a basis of size k which includes v.

    Thanks a lot for making it clear to me.

    → Reply