Sereja's blog

Codeforces Round #215 — tutorial
By Sereja, 10 years ago, translation, In English

Разбор задач Codeforces Round #215

368A - Sereja and Coat Rack

Each time we will go through the array and look for the minimal element which is not yet marked. If we find an item, we add it to the answer and mark it, otherwise we will subtract the penlty from answer.

368B - Sereja and Suffixes

We will count value ansi — number of different elements on the suffix from i. For calculation will walk from the end of the array, and we count ansi = ansi + 1 + newai, newai equals to 1, if element ai has not yet met and 0 otherwise.

367A - Sereja and Algorithm

If you look at what is written in the statment, it becomes clear that the algorithm finishes its work, if we can get a string like: xx, yy, zz, zyxzyxzyx... and all its cyclic shuffles. To check you just need to know the number of letters x, y and z separately. Quantities can be counted using partial sums.

367B - Sereja ans Anagrams

We will divide the sequence on min(n, p) sequences. 1-st, (1 + p)-th, (1 + 2·p)-th, ... element will go to the first sequence, 2-nd, (2 + p)-th, (2 + 2·p)-th... will go to the second sequence and so on. Now you need to find an answer for each of them, considering that p = 1. This can be solved by a simple method. You can go along the sequence from left to right and count the number of occurrences of each number. If the number of occurrences of each number will match the number of occurrences of the same number in the second sequence, then everything is OK.

367C - Sereja and the Arrangement of Numbers

Clear that we need to collect as many of the most expensive properties that would have been possible to build the array. Note that having n numbers, we have m = n·(n - 1) / 2 binding ties. See that this is a graph in which to do Euler path, adding as little as possible edges. For n%2 = 1 — everything is clear, and for n%2 = 0, you need to add an additional n / 2 - 1 rib. Why? This is your homework :)

The detailed explanation can be found here.

367D - Sereja and Sets

Replace out sets by array, where the element — the number set to which its index belongs. Now take all the consequitive sub-arrays with lengths of d and find a set of elements that were not found in that sub array. Clearly, if we as a response to select a subset of such set, it does not fit us. Remember all those "bad set." As we know all of them, we can find all the "bad" subsets. Now we choose the set with maximum count of elements which is not a bad set. It is better to work here with bit masks.

367E - Sereja and Intervals

We assume that the intervals are sorted, and in the end we will multiply the answer by n!, We can do so, as all segments are different.

Consider two cases n > m and n ≤ m. It would seem that you need to write different dynamics for them, but not difficult to show that in the first case the answer is always 0 . The second case is the following dynamics : dpi, l, r, i — how many numbers we have considered , l, r — only in this interval will be present number i. Also, we will need an additional dynamic si, l, i — how many numbers are considered , l — how many segments are already closed , and i does not belong to any segment . There will be 4 transfers, since every number we can not begin and end with more than one segment.

Now we should add x to our solution, it is quite simple: just add another parameter 0 / 1 in our dynamics, if we had such a element in the beginning of some interval or not. With out dynamics, it is not difficult.

For more details check out any solution that passed system tests.

  • Vote: I like it
  • +45
  • Vote: I do not like it

Comments Comments (14)
| Write comment?
»
10 years ago, # |
← Rev. 2   Vote: I like it +48 Vote: I do not like it

Sometimes I prefer to read the Russian tutorial, instead of the "Google Translated" one.

P.S.: I don't know Russian.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Next time change codeforces.ru to codeforces.com ayer than translate. It was hardliners to the Russian site in the initial blog.

    → Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Someone should write notes with Chinese

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could anyone please give a detailed explanation of problem B Div 1? I do not undestand why we can consider p = 1?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Split the sequence a into subsequences (vectors): subsequence ci is composed of numbers ai, ap + i, ..., akp + i (i < p). Then, we only need m consecutive elements of ci.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      why does it work fast? It will be O(p * m)?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        It's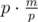

        Upd. Oh, yep, it's a crap.

        Upd2. Oh, no, it's really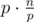 . Show why it's wrong, if it is.

        → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It's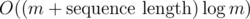 per every sequence ci which contains at least m elements; if a sequence contains less, we can just ignore it and not run any algorithm on it at all. There are at most 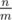such sequences, and the sum of their lengths is at most n, so it's 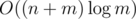amortized.

        → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have been working on "Sereja and Algorithm" for a few days, but I cannot see why we just need to count the number of x, y and z and compare them.

I understand that it's necessary, but I don't see why it's sufficient. Could someone explain that?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What you're asking about is whether it's always possible to rearrange the string to one of the form "zyxzyxz..". The algorithm doesn't specify any rules for which triples to rearrange (just that it can't be 'zyx' or its cyclic equivalents), so we can choose what's best for us.

    Imagine that there's a resulting string R, which is a permutation of letters of the input string S, and on which the algorithm terminates (the necessary condition).

    In every step, find the first position i in which S and R differ. It's obvious that the suffixes S[i..] and R[i..] will also be permutations of each other. Letter R[i] must appear in S somewhere later, let's say that S[j] = R[i]. Take the triple S[j - 1..j + 1] and rearrange (permute) it so that S[j] becomes S[j - 1]. This way, the wrong letter always moves one position left, without changing the prefix S[0..i - 1], so it eventually moves to S[i].

    Even if we can't choose the triple S[j - 1..j + 1] if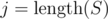 , we can just either choose S[j - 2..j] for i < j - 1, or for 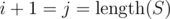permute the whole incorrect part of S (which is just 2 last letters plus the one between them) to become identical to the last triple in R.

    We see that a finite number of steps increases the longest common prefix of R and S by 1, so the 2 strings can be made equal.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thanks for your reply.

      Take the triple S[j - 1..j + 1] and rearrange

      What if S[j-1 .. j+1] is one of "zyx", "xzy", "yxz"?

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        There are more border cases to consider (and I'm sleepy), but the main idea is that you can keep taking triples which only contain the first 2 or last 2 letters of any substring that you can't choose, and shuffle those to turn it into a substring from which you can choose any triple.

        → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E has another nice solution, but I have absolutely no idea how to prove it, I found it through trail and error. Time complexity is $$$O(nm)$$$ — code

Basically it comes down to proving this: The number of sorted sequences of $$$n > 1$$$ segments such that the last segment is $$$[x,y]$$$ is $$$\frac{1}{n(n-1)}\binom{x-1}{n-1}\binom{y-1}{n-2}(ny-(n-1)x)$$$. Next, try all values of $$$y$$$ between $$$x$$$ and $$$m$$$ and all values of $$$k$$$ from 1 to $$$n$$$ — the index of the segment which has $$$x$$$ as its endpoint in the sorted sequence and apply the formula above.

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How does one come up with this formula?

    → Reply