710A - Ходы короля
Легко видеть, что в задаче возможно всего три случая. Если король находится углу доски, то у него 3 возможных хода. Если он стоит на краю доски, то у него 5 возможных хода (если конечно он не в углу). Наконец, если король не стоит на краю доски, то у него всего 8 возожных хода.
Сложность: O(1).
710B - Оптимальная точка на прямой
Легко видеть, что ответ всегд находится в одной из заданных точек (функция суммарного рассояния между парой заданных точек монотонна). Далее можно либо для каждой точки посчитать суммарное расстояние и выбрать оптимальную точку, либо заметить, что ответом является точка находящяяся посередине в отсортированном списке заданных точек (если точек чётное количетсво то слева посередине). Последний факт легко доказыватся, но можно это и не делать и сдать задачу первым способом.
Сложность: O(nlogn).
710C - Магический нечётный квадрат
Задачу предложил Resul Hangeldiyev Resul.
Решение задачи легко получить из второго примера. Легко видеть, что если расставить все нечётные числа в виде ромба посередине квадрата, то мы получим магический квадрат.
Сложность: O(n2).
710D - Две арифметические прогрессии
Эту задачу я уже давно хотел дать на раунд, она мне казалась очень стандартной, но я недооценил её сложность.
Запишем уравнение, которое описывает все решения задачи: a1k + b1 = a2l + b2 → a1k - a2l = b2 - b1. Имеем линейное диофантово уравнение с двумя неизвестными: Ax + By = C, A = a1, B = - a2, C = b2 - b1. Его решение имеет вид: 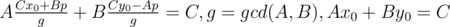 , где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям:
, где последнее уравнение решается с помощью расширенного алгоритма Евклида, а p произвольное целое число. Далее нам нужно удовлетворить двум условиям: 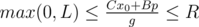 и
и 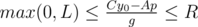 . Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
. Поскольку мы знаем знаки чисел A и B, последние уравнения задают отрезок возможных значений для переменной p, длина этого отрезка и является ответом на задачу.
Сложность: O(log(max(a1, a2))).
710E - Генерация строки
Задачу предложил Zi Song Yeoh zscoder.
У этой задачи есть простое решение, которое участники описали в комментариях. Моё решение несколько сложнее. Будем решать задачу с помощью динамического программирования. zn — наименьшее время, необходимое для получения n букв 'a'. Теперь рассмотрим переходы: переходы на дописывание одной буквы 'a' будем обрабатывать как обычно. Переходы на умножения на два и вычитание единицы будем обрабатыват одновременно: будем считать, что сразу после умножения числа i на двойку мы сразу сделаем i вычитаний и далее будем проталкивать от нашего числа вперёд такие обновления. Легко видеть, что такие обновления никогда не никогда не вкладываются, поэтому их можно хранить в очереди, дописывая очередное обновление в конец очереди, и, забирая лучшее обновление с начала очереди. Решение достаточно сложное на объяснение, но очень короткое, поэтому лучше посмотреть код :-)
Сложность: O(n).
710F - Операции над множеством строк
Задачу предложил Александр Кульков adamant.
Сначала научимся избавляться от запросов на удаление. В силу условия, что никакая строка не добавляется дважды (и, соответственно, не удаляется) нам достаточно посчитать ответ для всех добавленных строк (как будто они не удалялись) и вычесть из него ответ для уже удалённых. Таким образом, можно считать, что строки только добавляются.
Далее воспользуемся алгоритмом Ахо-Корасик. Единственная проблема, заключается в том, что алгоритм строит правильные суффиксные ссылки только после того как все строки добавлены. Чтобы решить эту проблему заметим, что ответ для набора строк равен ответу для некоторой части этого набора плюс ответ для оставшейся части. Далее воспользуемся стандартным приёмом превращения статической структуры данных (Ахо-Корасик в данном случае) в динамическую.
Пусть в данный момент в набор добавлено n строк, тогда мы будем хранить не более logn наборов строк размера разных степеней двойки. Добавим строку в набор размера нулевой степени двойки и далее перебрасывать наборы к большим степеням двойки, пока не получим инвариантный набор множеств.
Легко видеть, что каждая строка перебросится не более logm раз и на каждый запрос мы умеем отвечать за O(logm).
Сложность: O((slen + m)logm), где slen — суммарная длина всех строк во входном файле.







