Today I want to introduce you some very very useful data structures.
In this lecture, we are trying to improve your data structures skills, stay with us and click on read more. Important data structures :
Trees
Trees are one of the most useful data structures.A tree is a connected-acyclic graph.There are too many types of trees, like : rooted trees, weighted trees, directed trees, tries, etc.
Partial sum
There are two types of problems solvable by partial sum.
1.Problems which you are asked to answer some queries about the sum of a part of elements (without modify queries).
Solution of all of this problems are the same. You just need to know how to solve one of them.
Example : You are asked some queries on an array a1, a2, ...a, n. Each query give you numbers l and r and you should print al + al + 1 + ... + ar .
Solution : You need to build another array s1, s2, ..., sn which si = a1 + a2 + ... + ai and answer is sr - sl - 1 .
2.Problems which you are asked to perform some queries asking you to modify a part of elements (without printing queries.)
Solution of all of this problems are the same. You just need to know how to solve one of them.
Example : You need to perform some queries on an array a1, a2, ...a, n. Each query give you numbers l, r and v and for each i such that l ≤ i ≤ r you should increase ai by v, and then after performing all queries, you should print the whole array.
Solution : You should have another array p1, p2, ..., pn which, all of its members are initially 0, for each query, you should increase pl by v and decrease pr + 1 by v .
An then, for each i, starting from 1 you should increase pi by pi - 1. So, final array would be a1 + p1, a2 + p2, ..., an + pn .
Hard problem of partial sum : Troynacci Query
Disjoint sets
Disjoint sets are also useful data structures. Using them is fast and easy. We use theme in many algorithms, like Kruskal's and Prim's.
Disjoint sets, or DSU (Disjoint Sets Union) as their name, are sum sets. Imagine we have some boxes and some tools and initially each tool is in one box. Mostly, we are given some queries and ask to merge two boxes or print the members of a box or find which box is some tool in.
For rest of these, let's consider that initially there is exactly one tool in a box.That is, we have n tools and n boxes and initially, tool number i is in box number i.
For this propose, we can use so many containers.Like :
Trees
Trees are the most useful containers for DSU. For each vertex, we keep it's parent (and parrent of the root is -1). So, initially are parents are set to -1, and we have queries to find the root of each box(having the root, we can easily find the box's index) and queries for merging two trees. For better time complexity, every time we want to find the root of each vertex, we set it's parent to the root for the next queries.And while merging, we always want to minimize the height of the tree, so when we want to merge the boxes, it's like we put all the tools of the box with fewer tools in the other box.

The best way I've seen to code this kind of DSU, is style of bmerry : (C++)
int root(int v){return par[v] < 0 ? v : (par[v] = root(par[v]));}
void merge(int x,int y){ // x and y are some tools (vertices)
if((x = root(x)) == (y = root(y)) return ;
if(par[y] < par[x]) // balancing the height of the tree
swap(x, y);
par[x] += par[y];
par[y] = x;
}
In the code above, for each root v, par[v] equals the negative of number of tools in that box.
Arrays, vectors
We keep tools in a vector (or an array) and when we have a query to merge two boxes, we put all the tools of the box with fewer tools in the other box.
The time complexity is good because for each tool, we take and put it in an other box at most log(n) times (each time the size of the vector will be at least doubled).
So time complexity would be O(n.log(n)) .
Sets (red-black trees)
Other way is to keep them in a red-black tree (in C++ it's set). We do exactly like vectors, so time complexity would be O(n.log2(n)) . (One log is for inserting).
Problems : Hamro and tools, TROY Query (Join the group ACM-OI first)
Tries
Tries are some kind of rooted trees in which each edge has a character on it. Actually, trie is some kind of DFA (Determining Finite Automata). For a bunch of strings, their trie is the smallest rooted tree with a character on each edge and each of these strings can be build by writing down the characters in the path from the root to some node.
It's advantage is, LCP (Longest Common Prefix) of two of these strings is the LCA (Lowest Common Ancestor) of their nodes in the trie(a node that we can build the string by writing down the characters in the path from the root to that node).
Generating the trie :
Root is vertex number 0 (C++)
int x[MAX_NUMBER_OF_NODES][MAX_ASCII_CODE], next = 1; //initially all numbers in x are -1
void build(string s){
int i = 0, v = 0;
while(i < s.size()){
if(x[v][s[i]] == -1)
v = x[v][s[i++]] = next ++;
else
v = x[v][s[i++]];
}
}
Problem : A lot of games
Suffix array
Suffix array is a data structure that helps you sort all the suffixes in lexicography order.
This array consists of integers, the beginning of suffixes.
There are two ways to achieve this goal :
One) Non-deterministic algorithm : Use Robin-Carp and for check if a suffix is lexicographically less than another one, find their LCP using binary search + hash and then check the next character after their LCP.
Code :
namespace HashSuffixArray
{
const int
MAXN = 1 << 21;
typedef unsigned long long hash;
const hash BASE = 137;
int N;
char * S;
int sa[MAXN];
hash h[MAXN], hPow[MAXN];
#define getHash(lo, size) (h[lo] - h[(lo) + (size)] * hPow[size])
inline bool sufCmp(int i, int j)
{
int lo = 1, hi = min(N - i, N - j);
while (lo <= hi)
{
int mid = (lo + hi) >> 1;
if (getHash(i, mid) == getHash(j, mid))
lo = mid + 1;
else
hi = mid - 1;
}
return S[i + hi] < S[j + hi];
}
void buildSA()
{
N = strlen(S);
hPow[0] = 1;
for (int i = 1; i <= N; ++i)
hPow[i] = hPow[i - 1] * BASE;
h[N] = 0;
for (int i = N - 1; i >= 0; --i)
h[i] = h[i + 1] * BASE + S[i], sa[i] = i;
stable_sort(sa, sa + N, sufCmp);
}
} // end namespace HashSuffixArray
Two) Deterministic algorithm : We sort them log(MaxLength) steps, in the i - th step (counting from 0), we sort them according to their first 2i characters and put the suffixes whit the same prefix with 2i characters in the same buckets.
Code :
/*
Suffix array O(n lg^2 n)
LCP table O(n)
*/
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
#define REP(i, n) for (int i = 0; i < (int)(n); ++i)
namespace SuffixArray
{
const int MAXN = 1 << 21;
char * S;
int N, gap;
int sa[MAXN], pos[MAXN], tmp[MAXN], lcp[MAXN];
bool sufCmp(int i, int j)
{
if (pos[i] != pos[j])
return pos[i] < pos[j];
i += gap;
j += gap;
return (i < N && j < N) ? pos[i] < pos[j] : i > j;
}
void buildSA()
{
N = strlen(S);
REP(i, N) sa[i] = i, pos[i] = S[i];
for (gap = 1;; gap *= 2)
{
sort(sa, sa + N, sufCmp);
REP(i, N - 1) tmp[i + 1] = tmp[i] + sufCmp(sa[i], sa[i + 1]);
REP(i, N) pos[sa[i]] = tmp[i];
if (tmp[N - 1] == N - 1) break;
}
}
void buildLCP()
{
for (int i = 0, k = 0; i < N; ++i) if (pos[i] != N - 1)
{
for (int j = sa[pos[i] + 1]; S[i + k] == S[j + k];)
++k;
lcp[pos[i]] = k;
if (k)--k;
}
}
} // end namespace SuffixArray
(Codes by mukel)
Heaps
A heap is a binary rooted tree (a rooted tree that each node has at most 2 children) and each vertex has a value.
Heap property : Heap usually has a property, like the value of each vertex is equal to or greater than the value of its child(ren) (we call this a max heap). We can use heaps in heap sort.
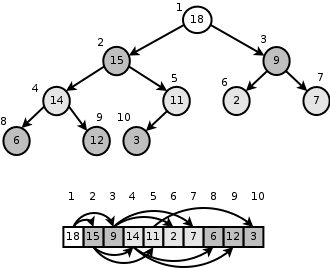
Fibonacci heaps
A fibonacci heap is a kind of heap with better complexities. We don't need to know what a fibonacci heap is.C++ already has one, priority_queue.
Binary Search Tree (BST)
A binary search tree (BST) is a binary rooted tree that every node has a value, and for each node, the value of every node in its left child's subtree is less than its value and the value of every node in its right child's subtree is greater than that. Usually we perform some queries on BSTs, like inserting, deleting, asking and ... .
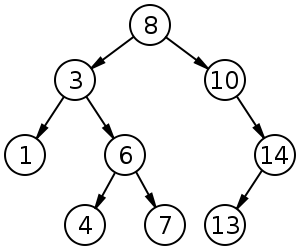
Binary search trees are too useful.
Red-black trees
A red-black tree is a kind of BST that after each query, BST will be balanced in such a way that it's height remains O(log(n)).
C++ already has a red-black tree inside, set .
You can read about them in C++ references.
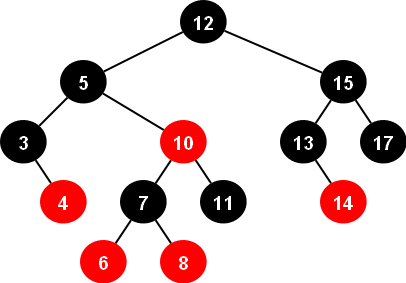
Unfortunately, set has not any function to find the k - th smallest minimum or find the index of an element, bust there is a data structure in C++ with does it in O(log(n))(also contains all set functions), tree :
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;
using namespace std;
template <typename T>
using ordered_set = tree<T, null_type, less<T>, rb_tree_tag, tree_order_statistics_node_update>;
int main(){
ordered_set<int> s;
s.insert(1);
s.insert(3);
cout << s.order_of_key(2) << endl; // the number of elements in the s less than 2
cout << *s.find_by_order(0) << endl; // print the 0-th smallest number in s(0-based)
}
(Thanks to HosseinYousefi for syntax using!)
This works even in C++ 98 !
You can read more about it, just google sgi STL.
SQRT Decomposition
Suppose we have an array a1, a2, ..., an and 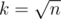 . We partition this array into k pieces each containing k elements of a.
. We partition this array into k pieces each containing k elements of a.
Doing this, we can do a lot of things in  . Usually we use them in the problems with modify and ask queries.
. Usually we use them in the problems with modify and ask queries.
Problems : Holes, DZY Loves Colors, RMQ (range minimum query) problem
Sparse Table
The main problem that we can solve is RMQ problem, we have an array a1, a2, ..., an and some queries. Each query gives you numbers l and r (l ≤ r) and you should print the value of min(al, al + 1, ..., ar) .
Solving using Sparse Table : For each i that 1 ≤ i ≤ n and for each j that 0 ≤ j and i + 2j - 1 ≤ n, we keep the value of min(ai, ai + 1, ..., ai + 2j - 1) in st[i][j] (preprocess) : (code is 0-based)
for(int j = 0;j < MAX_LOG;j++)
for(int i = 0; i < n;i ++)if(i + (1 << j) - 1 < n)
st[i][j] = (j ? min(st[i][j-1], st[i + (1 << (j-1)) - 1][j-1]): a[i]);
And then for each query, first of all, find the maximum x such that 2x ≤ r - l + 1 and answer is min(st[l][x], st[r - 2x + 1][x]) .
So, the main idea of Sparse Table, is to keep the value for each interval of length 2k (for each k).
You can use the same idea for LCA problem and so many other problems.
So preprocess will be in O(n.log(n)) and query will be in O(1)
Problems : Strip, GCDSSQ, LCM Query .
Heavy light decomposition
Heavy light decomposition is a way to partition a tree's vertices (or edges) in a good way.
In this kind of decomposition, we have some chains, and each vertex belongs to only one chain.
If vertex v is the parent of u size_of_subtree_of(v)/2 < size_of_subtree_of(u), u and v are in a chain and we call the edge uv, heavy, otherwise light.
There is at most one such child for each vertex v. If we consider the path from any vertex v to the root, there will be at most log(n) light edges there (go from v to the root, every time we see a light edge, size of subtree will be at least doubled). So, the number of chains on the way = O(log(n)) .
In each of these chains, we can contain a container or another data structure like segment tree or etc.

Problem : GRASS PLANTING
Fenwick
Suppose that we have n elements numbered from 1 to n.
Fenwick or BIT(Binary Indexed Tree) is a data structure with n nodes that node number i has some information about elements in the interval (i - i& - i, i] .
Actually, you don't need to know what each node contains. The only thing you should know, it this (then you can change and convert it) :
We have an array a1, a2, ..., an and all of them are initially 0. We are gives some queries, 1.increase ap by val and print a1 + a2 + ... + ap .
Only thing you should know is that how to solve this problem using Fenwick (and then you can change it and solve so many problems).
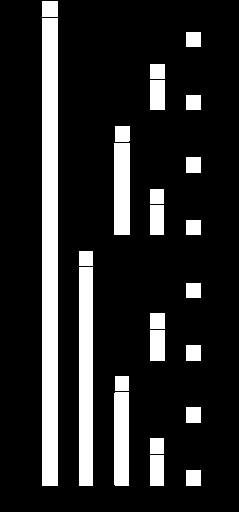
We perform each query in O(log(n)). Code : (1-based)
int fen[MAX_N];
void update(int p,int val){
for(int i = p;i <= n;i += i & -i)
fen[i] += val;
}
int sum(int p){
int ans = 0;
for(int i = p;i;i -= i & -i)
ans += fen[i];
return ans;
}
Please note that it should be 1-based. It can't be done 0-based.
Problems : Inversions, Pashmak and Parmida's problem, BST .
Segment tree
We have an array of elements and some queries on intervals. So, we will be glad if we can split this interval to O(log(n)) intervals that we have actually some information about them.
Segment tree does that for you. Segment tree is a tree that each of it's nodes belongs to an interval.
Root of the tree belongs to the interval [0, n) (0-based).
Each node, has 0 or two children. Left and right. If a node's interval is [l, r) and l + 1 ≠ r, the interval of its children will be [l, mid) and [mid, r) in order where  , so the height of this tree will be O(log(n)) .
, so the height of this tree will be O(log(n)) .

Each node has an index, we consider that root has index 1 and the children of a vertex x will have indices 2x and 2x + 1 in order.
Segment tree is the most useful data structure and every problem solvable by Fenwick is also solvable by Segment tree.
If the size of the root's interval is n, segment tree could have up to 4n nodes.
To split an interval to some nodes of this tree, we will act like this :
Suppose that S is the set of nodes which their union is [x, y) and no two different nodes in S have nonempty intersection.
A node i with interval [l, r) is in S if and only if x ≤ l ≤ r ≤ y and if it has a parent with interval [b, e), x > l or r > y .
C++ code :
vector<int> s;
void split(int x,int y, int id = 1,int l = 0, int r = n){// id is the index of the node
if(x >= r or l >= y) return ; // in this case, intersect of [l,r) and [x,y) is empty
if(x <= l && r <= y){
s.push_back(id);
return ;
}
int mid = (l+r)/2;
split(x,y,id * 2,l,mid);
split(x,y,id * 2 + 1,mid,r);
}
Example :
We have an array a1, a2, ..., an and q queries. There are 2 types of queries.
- S l r, Print al, al + 1, ..., ar
- M p x, Modify ap to x, it means ap = x .
First of all we need to build the segment tree, for each node we keep the sum of its interval, for node i we call it s[i], so we should build the initial segment tree.
void build(int id = 1,int l = 0,int r = n){
if(r - l < 2){ // l + 1 == r
s[id] = a[l];
return ;
}
int mid = (l+r)/2;
build(id * 2, l, mid);
build(id * 2 + 1, mid, r);
s[id] = s[id * 2] + s[id * 2 + 1];
}
So, before reading the queries, we should call build() .
Modify function :
void modify(int p,int x,int id = 1,int l = 0,int r = n){
s[id] += x - a[p];
if(r - l < 2){ // l = r - 1 = p
a[p] = x;
return ;
}
int mid = (l + r)/2;
if(p < mid)
modify(p, x, id * 2, l, mid);
else
modify(p, x, id * 2 + 1, mid, r);
}
(We should call modify(p, x))
Ask for sum function :
int sum(int x,int y,int id = 1,int l = 0,int r = n){
if(x >= r or l >= y) return 0;
if(x <= l && r <= y) return s[id];
int mid = (l+r)/2;
return sum(x, y, id * 2, l, mid) +
sum(x, y, id * 2 + 1, mid, r);
}
(We should call sum(l, r))
Lazy propagation
Imagine we have updates on intervals, what should we do ?
Example :
We have an array a1, a2, ..., an and q queries. There are 2 types of queries.
- S l r, Print al, al + 1, ..., ar
- I l r x, for each i such that l ≤ i < r, increase ai by x.
We shouldn't update all the nodes in this interval, just the maximal ones, then pass it to children when we need. This trick is called Lazy Propagation, so we should have another array lazy (for nodes) which are initially 0 and every time we want to perform increase query, increase lazy[id] with x.
As above, we also should have an array s for nodes.
So, build function will be same as above. But we need some more functions :
A function to update a node :
void upd(int id,int l,int r,int x){// increase all members in this interval by x
lazy[id] += x;
s[id] += (r - l) * x;
}
A function to pass the update information to its children :
void shift(int id,int l,int r){//pass update information to the children
int mid = (l+r)/2;
upd(id * 2, l, mid, lazy[id]);
upd(id * 2 + 1, mid, r, lazy[id]);
lazy[id] = 0;// passing is done
}
A function to perform increase queries :
void increase(int x,int y,int v,int id = 1,int l = 0,int r = n){
if(x >= r or l >= y) return ;
if(x <= l && r <= y){
upd(id, l, r, v);
return ;
}
shift(id, l, r);
int mid = (l+r)/2;
increase(x, y, v, id * 2, l, mid);
increase(x, y, v, id*2+1, mid, r);
s[id] = s[id * 2] + s[id * 2 + 1];
}
(We should call increase(l r x))
A function to answer to queries asking about the sum :
int sum(int x,int y,int id = 1,int l = 0,int r = n){
if(x >= r or l >= y) return 0;
if(x <= l && r <= y) return s[id];
shift(id, l, r);
int mid = (l+r)/2;
return sum(x, y, id * 2, l, mid) +
sum(x, y, id * 2 + 1, mid, r);
}
(We should call sum(l, r))
Problems : GSS1, GSS3, MULTQ3, DQUERY, KQUERY, POSTERS, PATULJCI, New Year Domino, Copying Data, DZY Loves Fibonacci Numbers, FRBSUM
Persistent data structures
Consider we have some elements, you perform some updates on it and then,and after performing all of them, you want to have the information about the elements, after each update.
For this propose, you got a data structure and somehow, you save the version of that data structure.
The most useful data structure for this propose is segment tree, I will explain persistent segment tree and all other data structures (like Fenwick) are like that.
Persistent segment tree
Example problem :
We have an array a1, a2, ..., an and at first q update queries and then u ask queries which you have to answer online.
Each update query gives you numbers p and v and asks you to increase ap by v .
Each ask query, gives you three numbers i and x and y and asks you to print the value of ax + ax + 1 + ... + ay after performing i - th query.
Each update query, changes the value of O(log(n)) nodes in the segment tree, so you should keep rest of nodes (not containing p) and create log(n) new nodes. Totally, you need to have q.log(n) nodes. So, you can not use normal segment's indexing, you should keep the index of children in the arrays L and R.
If you update a node, you should assign a new index to its interval (for i - th query).
You should keep an array root[q] which gives you the index of the interval of the root ( [0, n) ) after performing each query and a number ir = 0 which is its index in the initial segment tree (ans of course, an array s[MAXNODES] which is the sum of elements in that node). Also you should have a NEXT_FREE_INDEX = 1 which is always the next free index for a node.
First of all, you need to build the initial segment tree :
(In these codes, all arrays and queries are 0-based)
void build(int id = ir,int l = 0,int r = n){
if(r - l < 2){
s[id] = a[l];
return ;
}
int mid = (l+r)/2;
L[id] = NEXT_FREE_INDEX ++;
R[id] = NEXT_FREE_INDEX ++;
build(L[id], l, mid);
build(R[id], mid, r);
s[id] = s[L[id]] + s[R[id]];
}
(So, we should call build() )
Update function : (its return value, is the index of the interval in the new version of segment tree and id is the index of old one)
int upd(int p, int v,int id,int l = 0,int r = n){
int ID = NEXT_FREE_INDEX ++; // index of the node in new version of segment tree
if(r - l < 2){
s[ID] = (a[p] += v);
return ID;
}
int mid = (l+r)/2;
L[ID] = L[id], R[ID] = R[id]; // in case of not updating the interval of left child or right child
if(p < mid)
L[ID] = upd(p, v, L[ID], l, mid);
else
R[ID] = upd(p, v, R[ID], mid, r);
return ID;
}
(For the first query (with index 0) we should run root[0] = upd(p, v, ir) and for the rest of them, for j - th query se should run root[j] = upd(p, v, root[j - 1]) )
Function for ask queries :
int sum(int x,int y,int id,int l = 0,int r = n){
if(x >= r or l >= y) return 0;
if(x <= l && r <= y) return s[id];
int mid = (l+r)/2;
return sum(x, y, L[id], l, mid) +
sum(x, y, R[id], mid, r);
}
(So, we should print the value of sum(x, y, root[i]) )
Problems : Sign on Fence, MKTHNUM, COT, The Classic Problem











Thank you for this Useful toturial
thanks :)
Thanks for the article, especially for problems!
I didn't know that priority_queue is a Fibonacci heap. BTW, are you sure? cplusplus.com and cppreference say that push() works in logarithmic time.
P.S.1 This link (Hamro and tools problem in DSU section) gives access error: link
P.S.2 Isn't "sparse" a correct spelling?
As he said, you have to register youself in the ACM-OI group.
.
Great intro. Still have 1 question. Does order_set works only in g++? How it is going to work in Visual C++ ?
Yes. It's part of SGI STL extensions of G++.
Btw,
treeisn't part of C++ standard, it is extension of GNU C++. You can read more about this data structures here and here :)Also about persistent data structures. One can be interested in this: #TphcLk . Fully online, works with negative numbers also!)
. Fully online, works with negative numbers also!)
(k-th order statistics in the array segment using persistent bit trie.
Also you can use this structure to answer all queries from this problem.
How to apply your code to the XOR query please?
My full solution of Xor Queries: #QI8sxL
Xor query can be done greedy — we iterate through implicit bit trie of l..r subsegment and each time we try to take k-th bit in answer which is not equal to k-th bit in query.
Got it, thanks! The official solution is also based on trie. Any specific advantages over segment tree?
Actually segment tree is a kind of trie... Trie just a bit more generic
The is probably mistake in DSU implementation. par[x] += par[y] ??? What is this ?
Read it !
In the code above, for each root v, par[v] equals the negative of number of tools in that box.
So, par[x] = -sizeofbox(x), par[y] = -sizeofbox(y). so, par[x] + par[y] = -sizeofbox(x unuion y).
Have I understood it correct now ? par[v] shows the parent of v, if v is not the root, otherwise it shows negative number of nodes in group. 2 in 1 array!!!
Yep !
Actually there's an official name for the technique. It's called
union by rank. More info can be found here.Why are some comments in blue rectangles in codeforces (like the comment above) ?
It is new comments that you hadn't read before. If you update wepbage it'll be like any other comment
OK tnx :-)
I thought c++ priority queues are binary heap. As far as I remember Fibonacci heaps has huge constant factor. Could you share source where you get this information?
cplusplus.com thinks that
priority_queueis just a wrapper around push_heap/pop_heap/make_heap, which works with standard binary heap in a random access container and have logarithmic complexity.In my Visual C++ 2013 header of I have found make_heap and push_heap that use the same vector.
Maybe g++ uses Fibonacci heap. But it is no more part of STL. cplusplus.com usually hints if in different compilers something maybe different. Here it only states that priority_queue uses make_heap, push_heap, and pop_heap.
I also have found this.
Fenwick can be 0-based! Change
i+=i&-itoi|=i+1and changei-=i&-itoi=(i&(i+1))-1Why would I want to shoot in my foot :P?
Because e-maxx says so :)
Fenwick can be 12-based.
i+=i&-i->i += ((i-11)&-(i-11)):P:)
just in time :D thanx
At "Arrays, vectors", you said, "So time complexity would be O(n.log(n)) ."
However, I think the time complexity is O(n). The count of copied item is (1 + 2 + 4 + ... + N) where N < n and N = 2^k k is non-negative integer. So the count of copied item is (N * 2 — 1), if original array-modify involved, the count is (N * 2 — 1 + n). Time complexity is O(n).
Yes, and we can simply do vector.reserve(N) and problem disappears at all.
n = O(n.log(n)), I didn't say Θ(n.log(n))
And I think, the complexity will be O(nlogn) in cases where the merge operation is done like merge sort? And if we consider the merging two sets of size s1 and s2 takes O(s1+s2), is this the case?
In arrays, vectors what exactly we are doing can you please elaborate? Are we trying to implement Union-find DS using arrays or vectors? Are we using a vector at each index? So that at max each vertex has to placed O(logn) times? Thank you.
In case 2 of partial sum, can you apply your formula to binary index tree if sum within the range [l,r] is queried?
Yes. Just increase the value of al by v and increase the value of ar + 1 by - v (as I said in Fenwick).
Amazing! Thank you so much.
How to solve inversion count using BIT
For every number check how many numbers are before it? To do this, add numbers to BIT sorted from the largest to smallest.
Can you explain more?
Thank you very much for the great tutorial! :D
Dou you have any example in code of TRIES?
Thanx.
Refer this and this.
/
Nice blog/tutorial.. it would be useful for beginners as they will get an idea of what all to study.... Would have been nice if something like this was there when I started...
Good stuff. Cheers
Hi!
I don't get how suffix array (deterministic version) works.
Could you please give me some more clear description about it?
What does "tmp" store? It seems it contains something like [0,1,...,N-1], doesn't it?!
What about "pos"?
What's the initialization of "tmp"?
Thanks...
?!
http://codeforces.com/blog/entry/16541
Speaking of DSU, here's the same function, but in a more understandable way.
UPD: This is a way to compress paths, but not as efficient as the presented algorithm.
If you observe carefully, the code actually does update all the nodes in the path which is what you want to do.
the actual code compresses better All of the nodes parent will be the root but in crazzybeer's code it doesnt work also there is a closed bracket which leads to infinite loop
Mistake fixed. Now it should work. (Actually, this is the algorithm from Coursera so it works pretty well)
It works, but, I guess, it does a bit less work than the presented algorithm.
I see now. Thanks.
Do you actually want to express this idea?
Thank you for this Useful toturial.
What does the modify( p, x ) function do in the Segment tree section ?
"Modify ap to x, it means ap = x."
"The only thing you should know, it this (then you can change and convert it) :" I think "it" has to be "is",right?
Can please someone explain Partial sum part 2? What is the problem it solve? We need to find sum of elements of array a with indexes [l, r) ?
Thanks PrinceOfPersia for this very very useful article. :)
Note: please edit
line 1after R/B Tree imagebust-->but. :)how can multiple assignment modifications be done this way?please suggest an idea ,source code bingo !!
Is there a way to solve a problem which is same as partial sum instead of adding value, we need to change values in the interval [l,r] to v. Is there any good solution for this.
Segment Tree + Lazy Propagation
Astrologers proclaimed the Week of CodeChef Challenge. Amount of similar questions doubled.
In The persistent data structure function we should have a
s[id] = s[L[id]] + s[R[id]]; before the return statement
If the size of the root's interval is n, segment tree could have up to 4n nodes.How can we justify it? When I constructed an example, I got 2n-1 nodes.In what cases it will have 4n nodes.
Sorry, I didn't explain well in the previous post.
First, interval tree is balanced binary tree. So first level has 1 node, second 2, third 4... i-th level has 2^(i-1) nodes.
If your interval has lenght n, you must add some extra elements till n is not a power of two ( condition for balanced tree). Now the last level has m nodes (m=2^k) and higer levels have 2^(k-1) nodes, 2^(k-2) nodes... Sum of all nodes is 2^(k+1)-1. That is equal with 2m -1 nodes. The worst case is when n=2^x+1 and in that case you should have about 4n nodes, in best case if n=2^x you will have 2n-1 nodes.
I hope that now everything is clear.
thank you for this useful algorithms.
is there any other posts like this?
in Lazy propagation you had a function shift and function update.
what if we compare them?
like this:
and this is sum function:
In the given Trie code ( as posted by PrinceOfPersia) , It is only possible to search for prefix, How can we search if the word exist or not ?
You can add a boolean array, call it something like ends and initialize it to false, for each word you insert you set ends to true only in the last character of the word, so in your search method change the "return true" line to "return ends[v]". If you insert the word partition, if you look for part, it will return false, instead of true (which is what your code is doing).
You put this problem PATULJCI after explaining the segment tree with lazy propagation and before (Persistent).. but I can not solve it and my friend told me he solved it using (Persistent) segment tree!!!
could you please explain how to solve it without using Persistent ?!
I have no idea how to solve it with persistent!!!
This code is my friend's solution ( OmarHashim ) using persistent,
but i wanna know how to solve it without using persistent, could you please explain or give a hint on how to solve it?!!
UPD I got a O(N log N) solution with no segment tree at all, thanks :)
Hello, can you explain what are you doing , I have solved the problem using persistent segment tree(It was trivially a modification to MKTHNUM problem).
cntBit[i][j]=> means how many elements from 1 to i having 1 in the jth bit.you can see it's easy to construct that table in O(nlogn) time.
then when I get query [L,R] I iterate throw bits and see if there is more than (R-L+1)/2 elements having this bit 1, if so I set it, when I done I have a number every bit in it exists in more than siz/2 elements. so it is easy to notice that either this is the answer or there is no answer at all, to check if it is the answer or not, I count how many occurrences of this number in the interval [L,R] using binary search.
why adding -1 to i + (1 << (j-1)) in the code of sparse table?
I'll try to explain on small example.
Let's say that you have array of 10 elements, and you are on 3rd. If you want to increase 5 consecutive starting from position 3 you will have to increase elements on following positions: 3, 4, 5, 6, 7. You'd probably say 'ok, from 3 to 3+5=8', but that is not correct since 3 is considered to be one of these 5 consecutive elements.
Same is with sparse table. If you want to take 2^k consecutive elements starting from position i, last element is i+2^k-1 which is i+(1<<k)-1.
I believe it is an error. Let say i=4, j=1.
wonderful toturial:) can u please write one about DP?
Can somebody please explain how 444C - DZY Loves Colors is solved with sqrt decomposition? PrinceOfPersia
Hi! I have read that complexity of union find is
O(nlog*(n))but you have written that it's complexity isnlog(n).am i missing something?! (Can anybody help?!)it depends on the implementation, you will get
O(nlog*(n))if you do path compression, but he just mentions height balancing so the complexity will beO(nlog(n))Can any body tell me the condition when we can use lazy propagation on segment tree and when not ??
In persistent segment tree update function, i think you forgot this line of code at the end :
s[ID] = s[L[ID]] + s[R[ID]];
Why is it written as s[id] += (r — l) * x;
I am wondering why is the r-l factor there? Can someone help please
(r — l) is the length of segment [l , r) ! when we add x to each element in this segment the sum of this segment increase by (r — l) * x ! okay ?
In DSU implementation using arrays/vectors why will the size of set double every time? Example: if I have an array a[] = {a,b,c,d,e,f} and I put queries like merge(a,b), merge(b,c), merge(c,d), merge(d,e) merge(e,f) clearly it takes n-1 steps and so the size of array will increase by 1 in every step.
Also we are adding more tools to less tools to keep the height of tree less, correct me if I am wrong...
Got the answer to first question, the the author is taking about each tool.
There should be this line in the end of the update function in persistence segment tree. s[ID] = s[L[ID]] + s[R[ID]];
http://www.usaco.org/index.php?page=viewproblem2&cpid=576
Prefix sums style range modification on trees
Is there somebody who knows if it's better to merge the DSUs by height instead of by size? I think the height is more important because I think the complexity of the operating "finding the root" has more to do with the height of the tree.
In a lot of questions, we need the size of the sets.
Hence for the template, i would personally prefer 'union by size' over 'union by rank'.
after 3 years,now its 2018,and this blog is still read by many...thank you PrinceOfPersia
Thank you so much for this useful tutorial. Especially that DSU implementation — In the code above, for each root v, par[v] equals the negative of the number of tools in that box., love the way the how
pardoubles as thesize/rankarray, requiring only one array. Saved it as one of my snippets :)Wonderful !!!
Another problem on partial sum:- Queries from Pradnya wildcard 2019
thanx for this :)