Welcome to the new episode of PrinceOfPersia presents: Fun with algorithms ;)
You can find all the definitions here in the book "Introduction to graph theory", Douglas.B West. Important graph algorithms :
DFS
The most useful graph algorithms are search algorithms. DFS (Depth First Search) is one of them.
While running DFS, we assign colors to the vertices (initially white). Algorithm itself is really simple :
dfs (v):
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u)
color[v] = black
Black color here is not used, but you can use it sometimes.
Time complexity : O(n + m).
DFS tree
DFS tree is a rooted tree that is built like this :
let T be a new tree
dfs (v):
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u) and par[u] = v (in T)
color[v] = black
Lemma: There is no cross edges, it means if there is an edge between v and u, then v = par[u] or u = par[v].
Starting time, finishing time
Starting time of a vertex is the time we enter it (the order we enter it) and its finishing time is the time we leave it. Calculating these are easy :
TIME = 0
dfs (v):
st[v] = TIME ++
color[v] = gray
for u in adj[v]:
if color[u] == white
then dfs(u)
color[v] = black
ft[v] = TIME // or we can use TIME ++
It is useable in specially data structure problems (convert the tree into an array).
Lemma: If we run dfs(root) in a rooted tree, then v is an ancestor of u if and only if stv ≤ stu ≤ ftu ≤ ftv .
So, given arrays st and ft we can rebuild the tree.
Finding cut edges
The code below works properly because the lemma above (first lemma):
h[root] = 0
par[v] = -1
dfs (v):
d[v] = h[v]
color[v] = gray
for u in adj[v]:
if color[u] == white
then par[u] = v and dfs(u) and d[v] = min(d[v], d[u])
if d[u] > h[v]
then the edge v-u is a cut edge
else if u != par[v])
then d[v] = min(d[v], h[u])
color[v] = black
In this code, h[v] = height of vertex v in the DFS tree and d[v] = min(h[w] where there is at least vertex u in subtree of v in the DFS tree where there is an edge between u and w).
Finding cut vertices
The code below works properly because the lemma above (first lemma):
h[root] = 0
par[v] = -1
dfs (v):
d[v] = h[v]
color[v] = gray
for u in adj[v]:
if color[u] == white
then par[u] = v and dfs(u) and d[v] = min(d[v], d[u])
if d[u] >= h[v] and (v != root or number_of_children(v) > 1)
then the edge v is a cut vertex
else if u != par[v])
then d[v] = min(d[v], h[u])
color[v] = black
In this code, h[v] = height of vertex v in the DFS tree and d[v] = min(h[w] where there is at least vertex u in subtree of v in the DFS tree where there is an edge between u and w).
Finding Eulerian tours
It is quite like DFS, with a little change :
vector E
dfs (v):
color[v] = gray
for u in adj[v]:
erase the edge v-u and dfs(u)
color[v] = black
push v at the end of e
e is the answer.
Problems: 500D - New Year Santa Network, 475B - Strongly Connected City
BFS
BFS is another search algorithm (Breadth First Search). It is usually used to calculate the distances from a vertex v to all other vertices in unweighted graphs.
Code :
BFS(v):
for each vertex i
do d[i] = inf
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each w in adj[u]
if d[w] == inf
then d[w] = d[u] + 1, q.push(w)
Distance of vertex u from v is d[u].
Time complexity : O(n + m).
BFS tree
BFS tree is a rooted tree that is built like this :
let T be a new tree
BFS(v):
for each vertex i
do d[i] = inf
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each w in adj[u]
if d[w] == inf
then d[w] = d[u] + 1, q.push(w) and par[w] = u (in T)
SCC
The most useful and fast-coding algorithm for finding SCCs is Kosaraju.
In this algorithm, first of all we run DFS on the graph and sort the vertices in decreasing of their finishing time (we can use a stack).
Then, we start from the vertex with the greatest finishing time, and for each vertex v that is not yet in any SCC, do : for each u that v is reachable by u and u is not yet in any SCC, put it in the SCC of vertex v. The code is quite simple.
Shortest path
Shortest path algorithms are algorithms to find some shortest paths in directed or undirected graphs.
Dijkstra
This algorithm is a single source shortest path (from one source to any other vertices). Pay attention that you can't have edges with negative weight.
Pseudo code :
dijkstra(v) :
d[i] = inf for each vertex i
d[v] = 0
s = new empty set
while s.size() < n
x = inf
u = -1
for each i in V-s //V is the set of vertices
if x >= d[i]
then x = d[i], u = i
insert u into s
// The process from now is called Relaxing
for each i in adj[u]
d[i] = min(d[i], d[u] + w(u,i))
There are two different implementations for this. Both are useful (C++11).
One) O(n2)
int mark[MAXN];
void dijkstra(int v){
fill(d,d + n, inf);
fill(mark, mark + n, false);
d[v] = 0;
int u;
while(true){
int x = inf;
u = -1;
for(int i = 0;i < n;i ++)
if(!mark[i] and x >= d[i])
x = d[i], u = i;
if(u == -1) break;
mark[u] = true;
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second)
d[p.first] = d[u] + p.second;
}
}
Two) 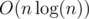
1) Using std :: set :
void dijkstra(int v){
fill(d,d + n, inf);
d[v] = 0;
int u;
set<pair<int,int> > s;
s.insert({d[v], v});
while(!s.empty()){
u = s.begin() -> second;
s.erase(s.begin());
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second){
s.erase({d[p.first], p.first});
d[p.first] = d[u] + p.second;
s.insert({d[p.first], p.first});
}
}
}
2) Using std :: priority_queue (better):
bool mark[MAXN];
void dijkstra(int v){
fill(d,d + n, inf);
fill(mark, mark + n, false);
d[v] = 0;
int u;
priority_queue<pair<int,int>,vector<pair<int,int> >, less<pair<int,int> > > pq;
pq.push({d[v], v});
while(!pq.empty()){
u = pq.top().second;
pq.pop();
if(mark[u])
continue;
mark[u] = true;
for(auto p : adj[u]) //adj[v][i] = pair(vertex, weight)
if(d[p.first] > d[u] + p.second){
d[p.first] = d[u] + p.second;
pq.push({d[p.first], p.first});
}
}
}
Problem: ShortestPath Query
Floyd-Warshall
Floyd-Warshal algorithm is an all-pairs shortest path algorithm using dynamic programming.
It is too simple and undrestandable :
Floyd-Warshal()
d[v][u] = inf for each pair (v,u)
d[v][v] = 0 for each vertex v
for k = 1 to n
for i = 1 to n
for j = 1 to n
d[i][j] = min(d[i][j], d[i][k] + d[k][j])
Time complexity : O(n3).
Bellman-Ford
Bellman-Ford is an algorithm for single source shortest path where edges can be negative (but if there is a cycle with negative weight, then this problem will be NP).
The main idea is to relax all the edges exactly n - 1 times (read relaxation above in dijkstra). You can prove this algorithm using induction.
If in the n - th step, we relax an edge, then we have a negative cycle (this is if and only if).
Code :
Bellman-Ford(int v)
d[i] = inf for each vertex i
d[v] = 0
for step = 1 to n
for all edges like e
i = e.first // first end
j = e.second // second end
w = e.weight
if d[j] > d[i] + w
if step == n
then return "Negative cycle found"
d[j] = d[i] + w
Time complexity : O(nm).
SPFA
SPFA (Shortest Path Faster Algorithm) is a fast and simple algorithm (single source) that its complexity is not calculated yet. But if m = O(n2) it's better to use the first implementation of Dijkstra.
The origin of this algorithm is unknown. It's said that at first Chinese coders used it in programming contests.
Its code looks like the combination of Dijkstra and BFS :
SPFA(v):
d[i] = inf for each vertex i
d[v] = 0
queue q
q.push(v)
while q is not empty
u = q.front()
q.pop()
for each i in adj[u]
if d[i] > d[u] + w(u,i)
then d[i] = d[u] + w(u,i)
if i is not in q
then q.push(i)
Time complexity : Unknown!.
MST
MST = Minimum Spanning Tree :) (if you don't know what it is, google it).
Best MST algorithms :
Kruskal
In this algorithm, first we sort the edges in ascending order of their weight in an array of edges.
Then in order of the sorted array, we add ech edge if and only if after adding it there won't be any cycle (check it using DSU).
Code :
Kruskal()
solve all edges in ascending order of their weight in an array e
ans = 0
for i = 1 to m
v = e.first
u = e.second
w = e.weight
if merge(v,u) // there will be no cycle
then ans += w
Time complexity : 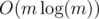 .
.
Prim
In this approach, we act like Dijkstra. We have a set of vertices S, in each step we add the nearest vertex to S, in S (distance of v from 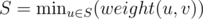 where weight(i, j) is the weight of the edge from i to j) .
where weight(i, j) is the weight of the edge from i to j) .
So, pseudo code will be like this:
Prim()
S = new empty set
for i = 1 to n
d[i] = inf
while S.size() < n
x = inf
v = -1
for each i in V - S // V is the set of vertices
if x >= d[v]
then x = d[v], v = i
d[v] = 0
S.insert(v)
for each u in adj[v]
do d[u] = min(d[u], w(v,u))
C++ code:
One) O(n2)
bool mark[MAXN];
void prim(){
fill(d, d + n, inf);
fill(mark, mark + n, false);
int x,v;
while(true){
x = inf;
v = -1;
for(int i = 0;i < n;i ++)
if(!mark[i] and x >= d[i])
x = d[i], v = i;
if(v == -1)
break;
d[v] = 0;
mark[v] = true;
for(auto p : adj[v]){ //adj[v][i] = pair(vertex, weight)
int u = p.first, w = p.second;
d[u] = min(d[u], w);
}
}
}
Two) 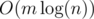
void prim(){
fill(d, d + n, inf);
set<pair<int,int> > s;
for(int i = 0;i < n;i ++)
s.insert({d[i],i});
int v;
while(!s.empty()){
v = s.begin() -> second;
s.erase(s.begin());
for(auto p : adj[v]){
int u = p.first, w = p.second;
if(d[u] > w){
s.erase({d[u], u});
d[u] = w;
s.insert({d[u], u});
}
}
}
}
As Dijkstra you can use std :: priority_queue instead of std :: set.
Maximum Flow
You can read all about maximum flow here.
I only wanna put the source code here (EdmondsKarp):
algorithm EdmondsKarp
input:
C[1..n, 1..n] (Capacity matrix)
E[1..n, 1..?] (Neighbour lists)
s (Source)
t (Sink)
output:
f (Value of maximum flow)
F (A matrix giving a legal flow with the maximum value)
f := 0 (Initial flow is zero)
F := array(1..n, 1..n) (Residual capacity from u to v is C[u,v] - F[u,v])
forever
m, P := BreadthFirstSearch(C, E, s, t, F)
if m = 0
break
f := f + m
(Backtrack search, and write flow)
v := t
while v ≠ s
u := P[v]
F[u,v] := F[u,v] + m
F[v,u] := F[v,u] - m
v := u
return (f, F)
algorithm BreadthFirstSearch
input:
C, E, s, t, F
output:
M[t] (Capacity of path found)
P (Parent table)
P := array(1..n)
for u in 1..n
P[u] := -1
P[s] := -2 (make sure source is not rediscovered)
M := array(1..n) (Capacity of found path to node)
M[s] := ∞
Q := queue()
Q.offer(s)
while Q.size() > 0
u := Q.poll()
for v in E[u]
(If there is available capacity, and v is not seen before in search)
if C[u,v] - F[u,v] > 0 and P[v] = -1
P[v] := u
M[v] := min(M[u], C[u,v] - F[u,v])
if v ≠ t
Q.offer(v)
else
return M[t], P
return 0, P
EdmondsKarp pseudo code using Adjacency nodes:
algorithm EdmondsKarp
input:
graph (Graph with list of Adjacency nodes with capacities,flow,reverse and destinations)
s (Source)
t (Sink)
output:
flow (Value of maximum flow)
flow := 0 (Initial flow to zero)
q := array(1..n) (Initialize q to graph length)
while true
qt := 0 (Variable to iterate over all the corresponding edges for a source)
q[qt++] := s (initialize source array)
pred := array(q.length) (Initialize predecessor List with the graph length)
for qh=0;qh < qt && pred[t] == null
cur := q[qh]
for (graph[cur]) (Iterate over list of Edges)
Edge[] e := graph[cur] (Each edge should be associated with Capacity)
if pred[e.t] == null && e.cap > e.f
pred[e.t] := e
q[qt++] : = e.t
if pred[t] == null
break
int df := MAX VALUE (Initialize to max integer value)
for u = t; u != s; u = pred[u].s
df := min(df, pred[u].cap - pred[u].f)
for u = t; u != s; u = pred[u].s
pred[u].f := pred[u].f + df
pEdge := array(PredEdge)
pEdge := graph[pred[u].t]
pEdge[pred[u].rev].f := pEdge[pred[u].rev].f - df;
flow := flow + df
return flow
Dinic's algorithm
Here is Dinic's algorithm as you wanted.
Input: A network G = ((V, E), c, s, t).
Output: A max s - t flow.
1.set f(e) = 0 for each e in E
2.Construct G_L from G_f of G. if dist(t) == inf, then stop and output f
3.Find a blocking flow fp in G_L
4.Augment flow f by fp and go back to step 2.
Time complexity : 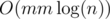 .
.
Theorem: Maximum flow = minimum cut.
Maximum Matching in bipartite graphs
Maximum matching in bipartite graphs is solvable also by maximum flow like below :
Add two vertices S, T to the graph, every edge from X to Y (graph parts) has capacity 1, add an edge from S with capacity 1 to every vertex in X, add an edge from every vertex in Y with capacity 1 to T.
Finally, answer = maximum matching from S to T .
But it can be done really easier using DFS.
As, you know, a bipartite matching is the maximum matching if and only if there is no augmenting path (read Introduction to graph theory).
The code below finds a augmenting path:
bool dfs(int v){// v is in X, it reaturns true if and only if there is an augmenting path starting from v
if(mark[v])
return false;
mark[v] = true;
for(auto &u : adj[v])
if(match[u] == -1 or dfs(match[u])) // match[i] = the vertex i is matched with in the current matching, initially -1
return match[v] = u, match[u] = v, true;
return false;
}
An easy way to solve the problem is:
for(int i = 0;i < n;i ++)if(match[i] == -1){
memset(mark, false, sizeof mark);
dfs(i);
}
But there is a faster way:
while(true){
memset(mark, false, sizeof mark);
bool fnd = false;
for(int i = 0;i < n;i ++) if(match[i] == -1 && !mark[i])
fnd |= dfs(i);
if(!fnd)
break;
}
In both cases, time complexity = O(nm).
Problem: 498C - Array and Operations
Trees
Trees are the most important graphs.
In the last lectures we talked about segment trees on trees and heavy-light decomposition.
Partial sum on trees
We can also use partial sum on trees.
Example: Having a rooted tree, each vertex has a value (initially 0), each query gives you numbers v and u (v is an ancestor of u) and asks you to increase the value of all vertices in the path from u to v by 1.
So, we have an array p, and for each query, we increase p[u] by 1 and decrease p[par[v]] by 1. The we run this (like a normal partial sum):
void dfs(int v){
for(auto u : adj[v])
if(u - par[v])
dfs(u), p[v] += p[u];
}
DSU on trees
We can use DSU on a rooted tree (not tree DSUs, DSUs like vectors).
For example, in each node, we have a vector, all nodes in its subtree (this can be used only for offline queries, because we may have to delete it for memory usage).
Here again we use DSU technique, we will have a vector V for every node. When we want to have V[v] we should merge the vectors of its children. I mean if its children are u1, u2, ..., uk where V[u1].size() ≤ V[u2].size() ≤ ... ≤ V[uk].size(), we will put all elements from V[ui] for every 1 ≤ i < k, in V[k] and then, V[v] = V[uk].
Using this trick, time complexity will be 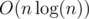 .
.
C++ example (it's a little complicated) :
typedef vector<int> vi;
vi *V[MAXN];
void dfs(int v, int par = -1){
int mx = 0, chl = -1;
for(auto u : adj[v])if(par - u){
dfs(u,v);
if(mx < V[u]->size()){
mx = V[u]->size();
chl = u;
}
}
for(auto u : adj[v])if(par - u and chl - u){
for(auto a : *V[u])
V[chl]->push_back(a);
delete V[u];
}
if(chl + 1)
V[v] = V[chl];
else{
V[v] = new vi;
V[v]->push_back(v);
}
}
LCA
LCA of two vertices in a rooted tree, is their lowest common ancestor.
There are so many algorithms for this, I will discuss the important ones.
Each algorithm has complexities < O(f(n)), O(g(n)) > , it means that this algorithm's preprocess is O(f(n)) and answering a query is O(g(n)) .
In all algorithms, h[v] = height of vertex v.
One) Brute force < O(n), O(n) >
The simplest approach. We go up enough to achieve the goal.
Preproccess :
void dfs(int v,int p = -1){
if(par + 1)
h[v] = h[p] + 1;
par[v] = p;
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}
Query :
int LCA(int v,int u){
if(v == u)
return v;
if(h[v] < h[u])
swap(v,u);
return LCA(par[v], u);
}
Two) SQRT decomposition 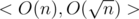
I talked about SQRT decomposition in the first lecture.
Here, we will cut the tree into  (H = height of the tree), starting from 0, k - th of them contains all vertices with h in interval
(H = height of the tree), starting from 0, k - th of them contains all vertices with h in interval 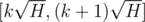 .
.
Also, for each vertex v in k - th piece, we store r[v] that is, its lowest ancestor in the piece number k - 1.
Preprocess:
void dfs(int v,int p = -1){
if(par + 1)
h[v] = h[p] + 1;
par[v] = p;
if(h[v] % SQRT == 0)
r[v] = p;
else
r[v] = r[p];
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}
Query:
int LCA(int v,int u){
if(v == u)
return v;
if(h[v] < h[u])
swap(v,u);
if(h[v] == h[u])
return (r[v] == r[u] ? LCA(par[v], par[u]) : LCA(r[v], r[u]));
if(h[v] - h[u] < SQRT)
return LCA(par[v], u);
return LCA(r[v], u);
}
Three) Sparse table 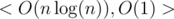
Let's introduce you an order of tree vertices, haas and I named it Euler order. It is like DFS order, but every time we enter a vertex, we write it's number down (even when we come from a child to this node in DFS).
Code for calculate this :
vector<int> euler;
void dfs(int v,int p = -1){
euler.push_back(v);
for(auto u : adj[v]) if(p - u)
dfs(u,v), euler.push_back(v);
}
If we have a vector<pair<int,int> > instead of this and push {h[v], v} in the vector, and the first time {h[v], v} is appeared is s[v] and s[v] < s[u] then LCA(v, u) = (mini = s[v]s[u]euler[i]).second.
For this propose we can use RMQ problem, and the best algorithm for that, is to use Sparse table.
Four) Something like Sparse table :) 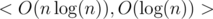
This is the most useful and simple (among fast algorithms) algorithm.
For each vector v and number i, we store its 2i-th ancestor. This can be done in 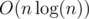 . Then, for each query, we find the lowest ancestors of them which are in the same height, but different (read the source code for understanding).
. Then, for each query, we find the lowest ancestors of them which are in the same height, but different (read the source code for understanding).
Preprocess:
int par[MAXN][MAXLOG]; // initially all -1
void dfs(int v,int p = -1){
par[v][0] = p;
if(p + 1)
h[v] = h[p] + 1;
for(int i = 1;i < MAXLOG;i ++)
if(par[v][i-1] + 1)
par[v][i] = par[par[v][i-1]][i-1];
for(auto u : adj[v]) if(p - u)
dfs(u,v);
}
Query:
int LCA(int v,int u){
if(h[v] < h[u])
swap(v,u);
for(int i = MAXLOG - 1;i >= 0;i --)
if(par[v][i] + 1 and h[par[v][i]] >= h[u])
v = par[v][i];
// now h[v] = h[u]
if(v == u)
return v;
for(int i = MAXLOG - 1;i >= 0;i --)
if(par[v][i] - par[u][i])
v = par[v][i], u = par[u][i];
return par[v][0];
}
Five) Advance RMQ < O(n), O(1) >
In the third approach, we said that LCA can be solved by RMQ.
When you look at the vector euler you see that for each i that 1 ≤ i < euler.size(), |euler[i].first - euler[i + 1].first| = 1.
So, we can convert the euler from its size(we consider its size is n + 1) into a binary sequence of length n (if euler[i].first - euler[i + 1].first = 1 we put 1 otherwise 0).
So, we have to solve the problem on a binary sequence A .
To solve this restricted version of the problem we need to partition A into blocks of size 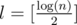 . Let A'[i] be the minimum value for the i - th block in A and B[i] be the position of this minimum value in A. Both A and B are
. Let A'[i] be the minimum value for the i - th block in A and B[i] be the position of this minimum value in A. Both A and B are 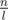 long. Now, we preprocess A' using the Sparse Table algorithm described in lecture 1. This will take
long. Now, we preprocess A' using the Sparse Table algorithm described in lecture 1. This will take 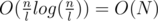 time and space. After this preprocessing we can make queries that span over several blocks in O(1). It remains now to show how the in-block queries can be made. Note that the length of a block is
time and space. After this preprocessing we can make queries that span over several blocks in O(1). It remains now to show how the in-block queries can be made. Note that the length of a block is 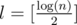 , which is quite small. Also, note that A is a binary array. The total number of binary arrays of size l is
, which is quite small. Also, note that A is a binary array. The total number of binary arrays of size l is 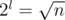 . So, for each binary block of size l we need to lock up in a table P the value for RMQ between every pair of indices. This can be trivially computed in
. So, for each binary block of size l we need to lock up in a table P the value for RMQ between every pair of indices. This can be trivially computed in 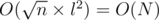 time and space. To index table P, preprocess the type of each block in A and store it in array
time and space. To index table P, preprocess the type of each block in A and store it in array 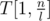 . The block type is a binary number obtained by replacing - 1 with 0 and + 1 with 1 (as described above).
. The block type is a binary number obtained by replacing - 1 with 0 and + 1 with 1 (as described above).
Now, to answer RMQA(i, j) we have two cases:
- i and j are in the same block, so we use the value computed in P and T
- i and j are in different blocks, so we compute three values: the minimum from i to the end of i's block using P and T, the minimum of all blocks between i's and j's block using precomputed queries on A' and the minimum from the beginning of j's block to j, again using T and P; finally return the position where the overall minimum is using the three values you just computed.
Six) Tarjan's algorithm O(na(n)) (a(n) is the inverse ackermann function)
Tarjan's algorithm is offline; that is, unlike other lowest common ancestor algorithms, it requires that all pairs of nodes for which the lowest common ancestor is desired must be specified in advance. The simplest version of the algorithm uses the union-find data structure, which unlike other lowest common ancestor data structures can take more than constant time per operation when the number of pairs of nodes is similar in magnitude to the number of nodes. A later refinement by Gabow & Tarjan (1983) speeds the algorithm up to linear time.
The pseudocode below determines the lowest common ancestor of each pair in P, given the root r of a tree in which the children of node n are in the set n.children. For this offline algorithm, the set P must be specified in advance. It uses the MakeSet, Find, and Union functions of a disjoint-set forest. MakeSet(u) removes u to a singleton set, Find(u) returns the standard representative of the set containing u, and Union(u, v) merges the set containing u with the set containing v. TarjanOLCA(r) is first called on the root r.
function TarjanOLCA(u)
MakeSet(u);
u.ancestor := u;
for each v in u.children do
TarjanOLCA(v);
Union(u,v);
Find(u).ancestor := u;
u.colour := black;
for each v such that {u,v} in P do
if v.colour == black
print "Tarjan's Lowest Common Ancestor of " + u +
" and " + v + " is " + Find(v).ancestor + ".";
Each node is initially white, and is colored black after it and all its children have been visited. The lowest common ancestor of the pair {u, v} is available as Find(v).ancestor immediately (and only immediately) after u is colored black, provided v is already black. Otherwise, it will be available later as Find(u).ancestor, immediately after v is colored black.
function MakeSet(x)
x.parent := x
x.rank := 0
function Union(x, y)
xRoot := Find(x)
yRoot := Find(y)
if xRoot.rank > yRoot.rank
yRoot.parent := xRoot
else if xRoot.rank < yRoot.rank
xRoot.parent := yRoot
else if xRoot != yRoot
yRoot.parent := xRoot
xRoot.rank := xRoot.rank + 1
function Find(x)
if x.parent == x
return x
else
x.parent := Find(x.parent)
return x.parent











Wow! Nice post! Please add Dinic's algorithm and an algorithm to find Euler tour to this list! I remember a problem which appeared on Euler tour here recently.
Done.
i think the answer is the reverse of e isn't it ? also you can add 508D to eulerian tours. thanks for the great tutorial :D
WTF? The reverse of an Eulerian tour is itself, isn't it ?
P.S: I was talking about bidirectional graphs.
well yes... but you should note that the starting point will be at the end, someone would make a mistake :D
It should be "sort" instead of solve. "solve all edges in ascending order of their weight in an array e." in the Kruskals Algorithm.
Great... Really very helpful post... Thanks a lot :)
what about bidirectional component searching algorithm?
It is modification of Ford-Bellman, so worst case complexity is O(nm), isn't it?
Also you didn't mention, but this algorithm also works for graphs with negative edges :)
The worst case is obvious, but important thing is its exact complexity(or at least average).
As mentioned above, it's easy to see, that this algo is just accurately written ford-bellman. So complexity is O(nm). It's easy to construct graph on which its complexity is C * n * m. For example full graph with
If you would go through edges always in decreasing order, then on every iteration every not satisfied vertex will be added to queue.
Once Burunduk1 told me that on average this algo works in $O(m log n)$, but i think this bound is from experience, i.e. not proved.
P.S. We always used this algo in finding MaxFlowMinCost, because it's easier to write than Dijkstra with potentials. And it works fast, because graph is changed on every step, so it's almost impossible to create anti-test(although i think once we've got TL...).
Could you show you MaxFlowMinCost code? I try to find something faster than O(V^3 * E)) and really dijkstra with potentials not to pleasant=)
do you have any mathematical proof for spfa algorithm?
Yeah I'm A Potato
Yeah I'm A Potato !!
"Bellman-Ford... ...(but if there is a cycle with negative weight, then this problem will be NP)."
Could you explain what you mean by NP?
We know that longest path is a NP-hard problem. When we can have negative cycles, then we have no condition at all, so we can multiply all weights by -1 (in longest path problem), and shortest path here, will be a longest path there. So this problem is NP-hard.
Actually, when we have a negative cycle there's no shortest path defined for vertices which are reachable from this cycle as we can go along the cycle unlimited number of times.
I believe PrinceOfPersia forgot to mention that he meant the longest simple path problem.
You are talking about shortest walk, shortest path is different. A path can't contain repeated vertex.
OK, then:)
Actually, I've never heard that shortest path problem states that the path must be simple. (And I've never heard of shortest walk either)
The "Finding cut vertices" pseudocode claims that the root of dfs is cut vertice in all cases where the root has 2 or more adjacent vertices. Instead, it should be that the root of dfs is cut vertice iff it has 2 or more children in the dfs tree.
Is there any difference ???
Think of a graph which is a cycle. Every vertice has 2 adjacent vertices, but every vertice has 1 child in dfs tree, except the last vertice reached by dfs which has no children in dfs tree.
The graph you are talking about doesn't have any cut vertex. My algorithm works fine.
P.S: I meant adj[v].size() is the number of children.
No, your algorithm returns that the root of the dfs is cut vertex, because it has 2 adjacent vertices.
Ok, you should clarify that adj[v].size() is the number of children in dfs tree because clearly adj[v] is the adjacency list of v in the graph, not adjacency list of v in the dfs tree.
Happy being in top contributors!
http://en.m.wikipedia.org/wiki/Tarjan%27s_off-line_lowest_common_ancestors_algorithm
Tarjan's Offline LCA algorithm is the LCA algorithm I usually use. It is based on dsu hence it costs O(n * a(n), O(1)), where a(n) is the inversw ackermann function. It is very essential and should be added to this post.
Thank you for your update. I'm surprised by your high efficiency!
For competitive programmers, I recommend the implementation of dsu below:
s[x] denotes parent of x
function f(x) finds the root of x
We can write
return x == s[x] ? x : s[x] = f(s[x]) as FIND
s[f(x)] = f(y) as UNION
With your union it works in ..
..
I read somewhere it's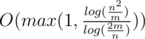 Where n is the number of union actions and m is the number of find queries.
Where n is the number of union actions and m is the number of find queries.
Great post!!! (Topological sort algoritms ;-) )
"haas and I named it Euler order." You and haas ?! Really ?! I doubt that :P But it was a fine post after all. :D Thanks :D
Why not ? In summer OI camp.
P.S: I didn't mean NAMED, meant called.
Then all your class CALLED it Euler order. Not just you and haas. :D
No, actually, he was teaching and I made up this name and said it, and since then every time haas wanted to talk about this order, he used it.
well written :)
In Dijkstra's algorithm using std::priority_queue is better to use the comparison function "greater <pair <int,int> >" instead of "less <pair <int,int> >" because takes less time to find the shortest path :).
what do you mean?
Is a DFS tree equivalent to a Union Find structure created using given edge pairs ?I am relatively new to graphs and find them similar :)
A simple typo: inversw ackermann function -> inverse ackermann function
I think there's no need to use color array in finding eulerian tour. You can visit each vertex several times.
What you mean by "Finding Eulerian tours"? I have some problems with terminology:)
Your code makes no sense for me while solving this problem — and one may call it Euler tour problem. Is it actually related to this technique instead? For a tree with 5 vertices and edges
your algorithm is printing 3-2-5-4-1. Can you please explain how is it related to Eulerian path/Eulerian tour/Eulerian cycle?
For SPFA you wrote
Time complexity : Unknown!.
This algorithm is modification of Bellman–Ford algorithm, and worst-case running time is O(V*E). It runs in O(E) on random graphs, but problem setter can actually make it run in O(V*E) if he isn't lazy to prepare good testcases :D
P.S. Thanks to Burunduk1 for teaching me how to actually create tests to make SPFA work in O(V*E) :)
Edit: Sorry, my old comment was irrelevant. I thought by SPFA you meant mincost-maxflow using SPFA..
If SPEA work in O(V*E) in worst-case , then it's better to use Bellman–Ford algorithm :) (when problemsetter like you ! )
Worst Test Case : Suppose one wants the shortest path from vertex 1 to vertex n. Then we can add edge (i, i + 1) with a small random weight for 1 ≤ i < n (thus the shortest path should be 1-2-...-n), and randomly add 4n other heavy edges. For this case, the so-called SPFA algorithm will be very slow.
How to make worst case tests for SFPA?
And is it recommended to use SFPA in general on Shortest Path Problems?
Yes, I accepted an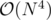 solution with N = 500 as I remember. Actually the tests was bad :D.
solution with N = 500 as I remember. Actually the tests was bad :D.
Can anyone link problems using tree sqrt decomposition
welcome to the Top 10 contribution list PrinceOfPersia :D
can't wait for more posts like this one
Nice work you've done :D
Thank you! Also it will be nice to see MaxFlowMinCost tutorial here.
I am going to learn a LCA algorithm and I have a question. @PrinceOfPersia, you wrote that Four) fourth method called : "Something like Sparse table" is " the most useful and simple (among fast algorithms) algorithm." Why it is better than third method where query takes O(1) instead of log(n) ? Is it because 3rd solution is hard to implement ?
Using 4-th method , what about adding new vertices to a tree ? After adding a vertex I have to recalculate everything, right ?
Because its code is much shorter and it's faster to type.
I think Path-based SC is also simple and it performs one DFS so it's faster.
In implementation of Dijkstra with priority, doesn't the size of queue grow much?
So, given arrays st and ft we can rebuild the tree.How we can build the tree?
How is the algorithm?
Could someone post practice problems that use the ideas behind each of those algorithms? Or perhaps link an existing post?
Thanks!
Can someone explain how complexity of DSU on trees is O(nlogn) ?
easy e-maxx, easy life
what do you mean??
Real fan of Justin Bieber
Nice post!
It was very useful for me. I hope that there are more users like me. Thanks very much.. :)
Please someone explain type 3(Sparse table), along with complexity, for finding LCA.
A sample code with pre-process and query would be of great help.
In type 3 after making euler vector we will find the node with minimum height such that it occur in euler vector between the position at which query node a & b comes first time in euler vector. logic behind this is if you observe in euler vector when query node a & b(let suppose a comes first in euler vector than b) then firstly there will be node of its child (in this case node with minimum height will be a if a is ancestor of b) and after completing dfs of its own it will go through the parent from where dfs of child is processing until b comes and in between a and b the node with minimum height will be LCA of a & b. there can not be any node b/w a & b with height less than LCA of a & b because a & b came into the dfs of LCA and parent of LCA came before starting the dfs of LCA and it will come again after completing dfs of LCA so it can't be present b/w a & b.
Time complexity will be O(n) for dfs and O(nlogn) for pre-processing of sparse table and query will be in O(1).
Hope it help here is my accepted code for problem LCA code i used the same logic with only one diff i used vector instead of vector<pair<int,int> > to store euler vector
Can someone explain why DSU on tree has O(nlogn) complexity... I understood the concept of DSU (in Kruskal) but could not have any clues about DSU on tree (in this post and http://www.codeforces.com/blog/entry/44351)
In Dijkstra Algorithm, using
std :: priority_queue,Declaration is priority_queue<pair<int,int>,vector<pair<int,int> >, less<pair<int,int> > > pq;
and during pushing in queue is pq.push({d[p.first], p.first});
Shouldn't it be
greater<pair<int,int>instead ofless<pair<int,int>, for getting minimum distance node first ?0 1 7 0 2 8 1 2 1 0 3 1 1 3 5 1 4 1 3 4 8 i am getting wrong output for this it should be greater instead of less
Can somebody add problems to the topics which lack practice problems?
You can use tags to find related problems. These are problems on Graphs sorted by the most solved (in decreasing order)
Is there a way to filter problems by algorithms on CodeForces? If not could somebody please give a list of Graph problems on each of these?
I believe this might sort out your problem :)
http://codeforces.com/problemset/tags/graphs?order=BY_SOLVED_DESC
for any other type of problems , just replace graphs with the keyword . Like if you want problems on dynamic programming , you can type
http://codeforces.com/problemset/tags/dp?order=BY_SOLVED_DESC
and many more ..
And even one of the website is also there which sorts out all problems of codeforces , spoj and other competitive coding websites i.e. www.a2oj.com
Second version of Dijkstra works in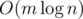 , not in
, not in 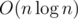 .
.
That's why O(n2) is also useful in case of dense graphs.
How to find cycle in an undirected graph?
https://e-maxx-eng.appspot.com/graph/depth-first-search.html#toc-tgt-2
Does cut edge algorithm work for parallel edges?
Nice collection. What about Min Cost Flow?
Thank PrinceOfPersia Good and informative
Anyone can suggest me a problem, where I've to detect all the nodes part of the negative cycle?
I am sorry but is that
parthe short form ofparents?Shouldn't the syntax of Priority Queue in Dijkstra code be:
priority_queue<pair<int,int>,vector<pair<int,int> >, greater<pair<int,int> > > pq;
Deleted