This is my first attempt at writing something useful, so your suggestions are welcome.
Most participants of programming contests are familiar with segment trees to some degree, especially having read this articles http://codeforces.com/blog/entry/15890, http://e-maxx.ru/algo/segment_tree (Russian only). If you're not — don't go there yet. I advise to read them after this article for the sake of examples, and to compare implementations and choose the one you like more (will be kinda obvious).
Segment tree with single element modifications
Let's start with a brief explanation of segment trees. They are used when we have an array, perform some changes and queries on continuous segments. In the first example we'll consider 2 operations:
- modify one element in the array;
- find the sum of elements on some segment. .
Perfect binary tree
I like to visualize a segment tree in the following way: image link
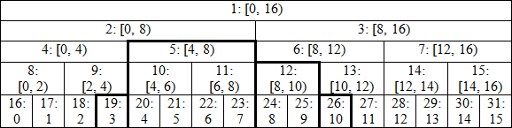
Notation is node_index: corresponding segment (left border included, right excluded). At the bottom row we have our array (0-indexed), the leaves of the tree. For now suppose it's length is a power of 2 (16 in the example), so we get perfect binary tree. When going up the tree we take pairs of nodes with indices (2 * i, 2 * i + 1) and combine their values in their parent with index i. This way when we're asked to find a sum on interval [3, 11), we need to sum up only values in the nodes 19, 5, 12 and 26 (marked with bold), not all 8 values inside the interval. Let's jump directly to implementation (in C++) to see how it works:
const int N = 1e5; // limit for array size
int n; // array size
int t[2 * N];
void build() { // build the tree
for (int i = n - 1; i > 0; --i) t[i] = t[i<<1] + t[i<<1|1];
}
void modify(int p, int value) { // set value at position p
for (t[p += n] = value; p > 1; p >>= 1) t[p>>1] = t[p] + t[p^1];
}
int query(int l, int r) { // sum on interval [l, r)
int res = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l&1) res += t[l++];
if (r&1) res += t[--r];
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", t + n + i);
build();
modify(0, 1);
printf("%d\n", query(3, 11));
return 0;
}
That's it! Fully operational example. Forget about those cumbersome recursive functions with 5 arguments!
Now let's see why this works, and works very efficient.
As you could notice from the picture, leaves are stored in continuous nodes with indices starting with n, element with index i corresponds to a node with index i + n. So we can read initial values directly into the tree where they belong.
Before doing any queries we need to build the tree, which is quite straightforward and takes O(n) time. Since parent always has index less than its children, we just process all the internal nodes in decreasing order. In case you're confused by bit operations, the code in build() is equivalent to
t[i] = t[2*i] + t[2*i+1].Modifying an element is also quite straightforward and takes time proportional to the height of the tree, which is O(log(n)). We only need to update values in the parents of given node. So we just go up the tree knowing that parent of node p is p / 2 or
p>>1, which means the same.p^1turns 2 * i into 2 * i + 1 and vice versa, so it represents the second child of p's parent.Finding the sum also works in O(log(n)) time. To better understand it's logic you can go through example with interval [3, 11) and verify that result is composed exactly of values in nodes 19, 26, 12 and 5 (in that order).
General idea is the following. If l, the left interval border, is odd (which is equivalent to l&1) then l is the right child of its parent. Then our interval includes node l but doesn't include it's parent. So we add t[l] and move to the right of l's parent by setting l = (l + 1) / 2. If l is even, it is the left child, and the interval includes its parent as well (unless the right border interferes), so we just move to it by setting l = l / 2. Similar argumentation is applied to the right border. We stop once borders meet.
No recursion and no additional computations like finding the middle of the interval are involved, we just go through all the nodes we need, so this is very efficient.
Arbitrary sized array
For now we talked only about an array with size equal to some power of 2, so the binary tree was perfect. The next fact may be stunning, so prepare yourself.
The code above works for any size n.
Explanation is much more complex than before, so let's focus first on the advantages it gives us.
- Segment tree uses exactly 2 * n memory, not 4 * n like some other implementations offer.
- Array elements are stored in continuous manner starting with index n.
- All operations are very efficient and easy to write.
You can skip the next section and just test the code to check that it's correct. But for those interested in some kind of explanation, here's how the tree for n = 13 looks like: image link
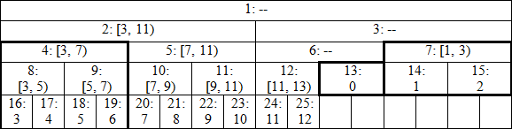
It's not actually a single tree any more, but a set of perfect binary trees: with root 2 and height 4, root 7 and height 2, root 12 and height 2, root 13 and height 1. Nodes denoted by dashes aren't ever used in query operations, so it doesn't matter what's stored there. Leaves seem to appear on different heights, but that can be fixed by cutting the tree before the node 13 and moving its right part to the left. I believe the resulting structure can be shown to be isomorphic to a part of larger perfect binary tree with respect to operations we perform, and this is why we get correct results.
I won't bother with formal proof here, let's just go through the example with interval [0, 7). We have l = 13, r = 20, l&1 => add t[13] and borders change to l = 7, r = 10. Again l&1 => add t[7], borders change to l = 4, r = 5, and suddenly nodes are at the same height. Now we have r&1 => add t[4 = --r], borders change to l = 2, r = 2, so we're finished.
Modification on interval, single element access
Some people begin to struggle and invent something too complex when the operations are inverted, for example:
- add a value to all elements in some interval;
- compute an element at some position.
But all we need to do in this case is to switch the code in methods modify and query as follows:
void modify(int l, int r, int value) {
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l&1) t[l++] += value;
if (r&1) t[--r] += value;
}
}
int query(int p) {
int res = 0;
for (p += n; p > 0; p >>= 1) res += t[p];
return res;
}
If at some point after modifications we need to inspect all the elements in the array, we can push all the modifications to the leaves using the following code. After that we can just traverse elements starting with index n. This way we reduce the complexity from O(nlog(n)) to O(n) similarly to using build instead of n modifications.
void push() {
for (int i = 1; i < n; ++i) {
t[i<<1] += t[i];
t[i<<1|1] += t[i];
t[i] = 0;
}
}
Note, however, that code above works only in case the order of modifications on a single element doesn't affect the result. Assignment, for example, doesn't satisfy this condition. Refer to section about lazy propagation for more information.
Non-commutative combiner functions
For now we considered only the simplest combiner function — addition. It is commutative, which means the order of operands doesn't matter, we have a + b = b + a. The same applies to min and max, so we can just change all occurrences of + to one of those functions and be fine. But don't forget to initialize query result to infinity instead of 0.
However, there are cases when the combiner isn't commutative, for example, in the problem 380C - Sereja and Brackets, tutorial available here http://codeforces.com/blog/entry/10363. Fortunately, our implementation can easily support that. We define structure S and combine function for it. In method build we just change + to this function. In modify we need to ensure the correct ordering of children, knowing that left child has even index. When answering the query, we note that nodes corresponding to the left border are processed from left to right, while the right border moves from right to left. We can express it in the code in the following way:
void modify(int p, const S& value) {
for (t[p += n] = value; p >>= 1; ) t[p] = combine(t[p<<1], t[p<<1|1]);
}
S query(int l, int r) {
S resl, resr;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l&1) resl = combine(resl, t[l++]);
if (r&1) resr = combine(t[--r], resr);
}
return combine(resl, resr);
}
Lazy propagation
Next we'll describe a technique to perform both range queries and range modifications, which is called lazy propagation. First, we need more variables:
int h = sizeof(int) * 8 - __builtin_clz(n);
int d[N];
h is a height of the tree, the highest significant bit in n. d[i] is a delayed operation to be propagated to the children of node i when necessary (this should become clearer from the examples). Array size if only N because we don't have to store this information for leaves — they don't have any children. This leads us to a total of 3 * n memory use.
Previously we could say that t[i] is a value corresponding to it's segment. Now it's not entirely true — first we need to apply all the delayed operations on the route from node i to the root of the tree (parents of node i). We assume that t[i] already includes d[i], so that route starts not with i but with its direct parent.
Let's get back to our first example with interval [3, 11), but now we want to modify all the elements inside this interval. In order to do that we modify t[i] and d[i] at the nodes 19, 5, 12 and 26. Later if we're asked for a value for example in node 22, we need to propagate modification from node 5 down the tree. Note that our modifications could affect t[i] values up the tree as well: node 19 affects nodes 9, 4, 2 and 1, node 5 affects 2 and 1. Next fact is critical for the complexity of our operations:
Modification on interval [l, r) affects t[i] values only in the parents of border leaves: l+n and r+n-1 (except the values that compose the interval itself — the ones accessed in for loop).
The proof is simple. When processing the left border, the node we modify in our loop is always the right child of its parent. Then all the previous modifications were made in the subtree of the left child of the same parent. Otherwise we would process the parent instead of both its children. This means current direct parent is also a parent of leaf l+n. Similar arguments apply to the right border.
OK, enough words for now, I think it's time to look at concrete examples.
Increment modifications, queries for maximum
This is probably the simplest case. The code below is far from universal and not the most efficient, but it's a good place to start.
void apply(int p, int value) {
t[p] += value;
if (p < n) d[p] += value;
}
void build(int p) {
while (p > 1) p >>= 1, t[p] = max(t[p<<1], t[p<<1|1]) + d[p];
}
void push(int p) {
for (int s = h; s > 0; --s) {
int i = p >> s;
if (d[i] != 0) {
apply(i<<1, d[i]);
apply(i<<1|1, d[i]);
d[i] = 0;
}
}
}
void inc(int l, int r, int value) {
l += n, r += n;
int l0 = l, r0 = r;
for (; l < r; l >>= 1, r >>= 1) {
if (l&1) apply(l++, value);
if (r&1) apply(--r, value);
}
build(l0);
build(r0 - 1);
}
int query(int l, int r) {
l += n, r += n;
push(l);
push(r - 1);
int res = -2e9;
for (; l < r; l >>= 1, r >>= 1) {
if (l&1) res = max(res, t[l++]);
if (r&1) res = max(t[--r], res);
}
return res;
}
Let's analyze it one method at a time. The first three are just helper methods user doesn't really need to know about.
Now that we have 2 variables for every internal node, it's useful to write a method to apply changes to both of them. p < n checks if p is not a leaf. Important property of our operations is that if we increase all the elements in some interval by one value, maximum will increase by the same value.
build is designed to update all the parents of a given node.
push propagates changes from all the parents of a given node down the tree starting from the root. This parents are exactly the prefixes of p in binary notation, that's why we use binary shifts to calculate them.
Now we're ready to look at main methods.
As explained above, we process increment request using our familiar loop and then updating everything else we need by calling build.
To answer the query, we use the same loop as earlier, but before that we need to push all the changes to the nodes we'll be using. Similarly to build, it's enough to push changes from the parents of border leaves.
It's easy to see that all operations above take O(log(n)) time.
Again, this is the simplest case because of two reasons:
- order of modifications doesn't affect the result;
- when updating a node, we don't need to know the length of interval it represents.
We'll show how to take that into account in the next example.
Assignment modifications, sum queries
This example is inspired by problem Timus 2042
Again, we'll start with helper functions. Now we have more of them:
void calc(int p, int k) {
if (d[p] == 0) t[p] = t[p<<1] + t[p<<1|1];
else t[p] = d[p] * k;
}
void apply(int p, int value, int k) {
t[p] = value * k;
if (p < n) d[p] = value;
}
These are just simple O(1) functions to calculate value at node p and to apply a change to the node. But there are two thing to explain:
We suppose there's a value we never use for modification, in our case it's 0. In case there's no such value — we would create additional boolean array and refer to it instead of checking
d[p] == 0.Now we have additional parameter k, which stands for the lenght of the interval corresponding to node p. We will use this name consistently in the code to preserve this meaning. Obviously, it's impossible to calculate the sum without this parameter. We can avoid passing this parameter if we precalculate this value for every node in a separate array or calculate it from the node index on the fly, but I'll show you a way to avoid using extra memory or calculations.
Next we need to update build and push methods. Note that we have two versions of them: one we introduces earlier that processes the whole tree in O(n), and one from the last example that processes just the parents of one leaf in O(log(n)). We can easily combine that functionality into one method and get even more.
void build(int l, int r) {
int k = 2;
for (l += n, r += n-1; l > 1; k <<= 1) {
l >>= 1, r >>= 1;
for (int i = r; i >= l; --i) calc(i, k);
}
}
void push(int l, int r) {
int s = h, k = 1 << (h-1);
for (l += n, r += n-1; s > 0; --s, k >>= 1)
for (int i = l >> s; i <= r >> s; ++i) if (d[i] != 0) {
apply(i<<1, d[i], k);
apply(i<<1|1, d[i], k);
d[i] = 0;
}
}
Both this methods work on any interval in O(log(n) + |r - l|) time. If we want to transform some interval in the tree, we can write code like this:
push(l, r);
... // do anything we want with elements in interval [l, r)
build(l, r);
Let's explain how they work. First, note that we change our interval to closed by doing r += n-1 in order to calculate parents properly. Since we process our tree level by level, is't easy to maintain current interval level, which is always a power of 2. build goes bottom to top, so we initialize k to 2 (not to 1, because we don't calculate anything for the leaves but start with their direct parents) and double it on each level. push goes top to bottom, so k's initial value depends here on the height of the tree and is divided by 2 on each level.
Main methods don't change much from the last example, but modify has 2 things to notice:
- Because the order of modifications is important, we need to make sure there are no old changes on the paths from the root to all the nodes we're going to update. This is done by calling push first as we did in query.
- We need to maintain the value of k.
void modify(int l, int r, int value) {
if (value == 0) return;
push(l, l + 1);
push(r - 1, r);
int l0 = l, r0 = r, k = 1;
for (l += n, r += n; l < r; l >>= 1, r >>= 1, k <<= 1) {
if (l&1) apply(l++, value, k);
if (r&1) apply(--r, value, k);
}
build(l0, l0 + 1);
build(r0 - 1, r0);
}
int query(int l, int r) {
push(l, l + 1);
push(r - 1, r);
int res = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
if (l&1) res += t[l++];
if (r&1) res += t[--r];
}
return res;
}
One could notice that we do 3 passed in modify over almost the same nodes: 1 down the tree in push, then 2 up the tree. We can eliminate the last pass and calculate new values only where it's necessary, but the code gets more complicated:
void modify(int l, int r, int value) {
if (value == 0) return;
push(l, l + 1);
push(r - 1, r);
bool cl = false, cr = false;
int k = 1;
for (l += n, r += n; l < r; l >>= 1, r >>= 1, k <<= 1) {
if (cl) calc(l - 1, k);
if (cr) calc(r, k);
if (l&1) apply(l++, value, k), cl = true;
if (r&1) apply(--r, value, k), cr = true;
}
for (--l; r > 0; l >>= 1, r >>= 1, k <<= 1) {
if (cl) calc(l, k);
if (cr && (!cl || l != r)) calc(r, k);
}
}
Boolean flags denote if we already performed any changes to the left and to the right. Let's look at an example: image link
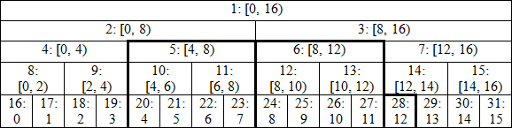
We call modify on interval [4, 13):
- l = 20, r = 29, we call apply(28);
- l = 10, r = 14, we call calc(14) — first node to the right of current interval is exactly the parent of last modified node;
- l = 5, r = 7, we call calc(7) and then apply(5) and apply(6);
- l = 3, r = 3, so the first loop finishes.
Now you should see the point of doing --l, because we still need to calculate new values in nodes 2, 3 and then 1. End condition is r > 0 because it's possible to get l = 1, r = 1 after the first loop, so we need to update the root, but --l results in l = 0.
Compared to previous implementation, we avoid unnecessary calls calc(10), calc(5) and duplicate call to calc(1).











Is lazy propagation possible this way?
Of course. Modification is more complex of course, but almost all principles are already described.
I just want to polish the implementation before posting.
i most of the time use this method of segment tree & i also coded lazy propagation! :)
I tried lazy propagation for long but couldn't code the iterative version of it. Can you share your code for iterative lazy propagation?
Can You share your implementation
can you share your code about the range update?
atcoder's impl is nice
Also for reference: Urbanowicz's post about non-recursive segment tree implementation: https://codeforces.com/blog/entry/1256
Thanks ! First time I know something new that segment tree with no-recursive .
True, my implementation is basically a refinement of the one in that post and in goo.gl_SsAhv's comment to that post. But for some reason it's still not well known and not really searchable, and I wasn't aware of that post. Also I hope to provide more knowledge, especially after I add the section about lazy propagation.
Just wondering, how did you write codes like this?
for (t[p += n] = value; p > 1; p >>= 1) t[p>>1] = t[p] + t[p^1];
Did you write it in the first attempt or you wrote something else and compressed that?
I don't remember, but of course it wasn't the first version, the code was revisited several times.
I think at first it looked like the code as I posted for non-commutative combiners, which is also used in build method.
^1 trick is used in max flow implementation where edge is stored adjacent to it's reverse, so we can use ^1 to get from one to another. I'm not sure, but probably it came from there.
I believe smth like this is more understandable and is equivalently short:
Well, it's a matter of style. I prefer not to write modifications inside a loop condition.
I'm just saying that this way it's more similar to traditional segment tree implementation and thus easier to follow the logic. But you are right, it's just a matter of style :)
it so useful for non-red participants
Hello, can you explain this line ? ~~~~~ t[p>>1] = t[p] + t[p^1] ~~~~~
Specifically, why are you xor-ing it?
p>>1 is a parent of p in the tree. Another son of p>>1 is p^1, since x^1 gives you x with reversed parity(last bit).
So basically, p^1 equals p/2 + 1 ?
No, p^1 equals to p+1 if p is even, and p-1 if p is odd.
xor will give the other child of the parent. For example if p is left child, p^1 will give the right one. Quite an interesting way of doing this in fact.
Thank you!
Hello, sorry to ask another silly question. Al.Cash says :
"l, the left interval border, is odd (which is equivalent to l&1)”
I am not familiar with bit operations too much, and I am having difficulty how
x AND 1gives odd/even value. Thanks in advance :)Every odd value ends with 1(3 = 11, 5 = 101) and every even value ends with 0(2 = 10, 4 = 100).
Hi, I am new in competitive programming, I was reading this article and trying to use it , but i dont understand how the function query works, for example if I have these numbers 1 47 45 23 348 and I would like the sum from 47 to 23, whats numbers should I put in the arguments???? please help, thanks
well your array starts from position 0. Position of 47 is 1 and of 23 is 3. The Query will give you an answer for [l, r) so you should pass as arguments (1, 4). Hope it helps!
Section about lazy propagation has been added.
I did some speed comparison between recursive and non-recursive lazy segment trees. With array size of 1<<18 and 1e7 randomly chosen operations between modifications and queries. Array size of 1<<18 is of course easier for my recursive code which uses arrays of the size 2^n but on practise it doesn't affect much to the speed of the code.
My recursive ( http://paste.dy.fi/BUZ ): 6 s
Non-recursive from the blog: ( http://paste.dy.fi/kBY ): 3 s
That's quite big difference in my opinion. Unfortunately the non-recursive one seems to be a bit more painful to code but maybe it's just that I'm used to code it recursively.
I think your modification on all element in an interval is not incrementing every element in an interval.You should check it.
Ex: n=8 0 1 2 3 4 5 6 7 modif(0,8,5); It should increment all places by 5.According to your algorithm array t is- 33 6 22 1 5 9 13 0 1 2 3 4 5 6 7
but clearly all element isn't incremented by 5.
Probably you're talking about the last example, but the operation there is assignment, not increment. And array looks absolutely correct except it should start with 40 not 33 (I believe 33 is a typo — let me know if it's not the case).
That's the point of 'lazy propagation' — not to modify anything until we really need it. You shouldn't access tree elements directly unless you called push(0, 8).
I was talking about this modify function: void modify(int l, int r, int value) { for (l += n, r += n; l < r; l >>= 1, r >>= 1) { if (l&1) t[l++] += value; if (r&1) t[--r] += value; } }
I see. Again, if you want to get an element — call query, don't access the tree directly. And you don't need to call build in this example.
Is it possible to extend this form to Multiple dimensions !
Sure, just change one loop everywhere into two nested loops for different coordinates.
Is it possible to implement lazy propogation in 2D?
How to perform find-kth query? For n that is not the power of 2.
One way is to make it next power of two and fill rest with zeros. Then the K-th one query can be calculated iteratively as:
could you explain how this is correct or how it works?
Hi. I have a question. When should it be considered necessary to use lazy propagation?
When you have both range modifications and range queries, or just range modifications for which order is important (for example, assignment).
Understood. + for you!
Can anyone please explain how the code in section "Modification on interval, single element access" actually work with a small example if possiple explaining how to we get sum over a range after the update(which also I am not able to understand!) ?
This example doesn't support getting sum over a range, only single element access (I was hoping it's clear from the heading). It only shows that sometimes we can invert basic operations, but for more complex operations you need lazy propagation.
can you give an example of single element access after some update , i am not able to grasp how query() would return a[p] (as u mentioned in some earlier comment to call query to access an element or simply what does the query() do ?
query() doesn't simply access the element — it calculates it as a sum of all the updates applied to that element.
Can someone explain logic(bit operations) here (t[p += n] = value; p > 1; p >>= 1)
The above expression is from the below function void modify(int p, int value) { // set value at position p for (t[p += n] = value; p > 1; p >>= 1) t[p>>1] = t[p] + t[p^1]; }
It is equivalent to this simplified code:
For the explanation of using xor(^) you can check the previous comment that I made.
Can u explain query function a bit more clearly Thanks for ur previous answer
Thanks for this post, it is very useful for beginners like me. But there is a small problem; the picture of the segment tree at the very beginning of the post is not showing. It would be nice if you fixed that :)
Please can somebody explain how to change all the elements of an array in an interval [l,r]to a constant value v using lazy propagation.
Thanks.
The last example does exactly that, assignment on an interval.
how to scale values in a given range say [L,R] with constant C by segment tree or BIT . Thanks in advance :D
I dont know for BIT but for segtree you can store additional
factorfor all nodes (initialized by 1). For each scale query, just scale this factor properties as always.I have a little question. In this problem, 533A — Berland Miners, I used this. I used this before, so I thought it works perfectly.
My submission with N = 106 + 5 got WA. When I changed it to N = 220, it took AC.
N = 106 + 5 --> http://codeforces.com/contest/533/submission/12482628
N = 220 --> http://codeforces.com/contest/533/submission/12483080
220 is bigger than 106 + 5 but problem isn't this. I tried it with N = 2 * 106 + 5 but I got WA again.
N = 2 * 106 + 5 --> http://codeforces.com/contest/533/submission/12483105
Do you have any idea about it?
As said in this post:
Not sure, where exactly that fails for you, but I guess it's here:
Seems like you intend to take left child of
opand right child ofcl, but when you have a set of trees it doesn't always work.I didn't understand the problem on here. Is it different from maximum of range or another segment operation?
But it works with N = 3·106 + 5... 12484538
I think the problem is in this line:
if(op[1] == 0)Node 1 is a true root only if N is a power of 2, otherwise it's not trivial to define what's stored there (just look at the picture).
Everything is guaranteed to work only if you use queries and don't access tree element directly (except for leaves).
Great and efficient implementation. Could you please say more about "Modification on interval [l, r) affects t[i] values only in the parents of border leaves: l+n and r+n-1.". Because, the inc method modifies more than the parents of the border leaves.
If I well understood, you want to explain the fact that in query method (max implementation) we need only to push down ONLY to the left border and right border nodes. Since when computing the query we will be using only the nodes along the route. Moreover, this explains the fact that when we finish increment method, we need ONLY to propagate up to to root of the tree starting from the left and right border leaves, so that the tree and the lazy array will be consistent and representing correct values.
You're right. I wanted to say what values are affected except the ones we modify directly in the loop (the ones that compose the interval). Will think how to formulate it better.
If you prefer closed interval, just change
r += ntor += n+1, otherwise it's easy to make mistakes.You said that range modifications and point updates are simple, but the following test case doesn't give a correct example (if I understood the problem correctly): - 5 nodes - 1 2 4 8 16 are t[n, n + 1, n + 2, n + 3, n + 4] - one modification: add 2 to [0, 5) - query for 0
returns 59, while it should be 3.
Code (same as all the functions given above, but for unambiguity:
Input: 5 1 2 4 8 16
Just remove build — it doesn't belong to this example.
Al.Cash , I am finding the code inside the header of for-loop too confusing, Can you please tell me the easy and the common version of theirs ?
Like this :
What does it mean ? Its tough for me to understand. Would be great if you could clarify this.
Thanks Alot. PS. Nice work on the tutorial, CF needs more articles like this one :)
Step-by-step, in the simpler case (when n = 2k and we have full binary tree). Consider n = 16:
landrfrom [0, 16], as outer world does not know anything about tree representation — it gives is bounds of the query.foris executed exactly once before any iteration (as per definition). That is: add n (16 in our case) to bothlandr, i.e. convert "array coordinates" to numbers of vertices in the tree.landrby two.>>= 1means "bitwise shift by one bit", which works exactly like division by two with rounding down for non-negative integers.5 elements. (Read as 'count of 0 is 5') 0->5 1->0 2->0 3->0 4->0. Therefore for query <1, the answer should be 4 cuz 4 slots have value <1 (1,2,3 and 4).
according to this implementation when array is not of size 2^n, the tree is coming out to be wrong. n=5. so we start filling at n=5.
We have 4 slots with value [0,1) and 1 slot with value [5-6). The array would be like: (started filling at 5 cuz n=5, representing [0,1)) 0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 4 0 0 0 0 1
now when making segment for array index 10, the value at index 5 gets overwritten. How to handle this?
To this line
I have a question: If the apply operation does not satisfy the associative law, is it still work?
For example:
modify(3, 11, value1)1 If I use push(3, 11), operations on node 5 is:
1.1 apply(2, d[2]); ( in the
pushloop);1.2 d[5] += d[2] ( in the
apply);1.3 d[2] is passed to 5's son, d[5] = 0 (in the
apply(5, d[5]);1.4 d[5] = value (in the
modifyloop);...
value is passed to 5's son 10 and 11, so:
1.5 d[10] = (d[10] + d[2]) + value; ( same to 11)
2 If I use push(3, 4), push(10, 11), operations on node 5 is:
2.1 apply(2, d[2]); (in the
pushloop);2.2 d[5] += d[2]; (in the
apply);2.3 d[5] += value; (in the
modifyloop);...
d[5] is passed to 5's son 10 and 11, so:
2.4 d[10] = d[10] + (d[2] + value);
1.5 is equal to 2.4, because (a+b)+c = a+(b+c), but if I replace the
+to other special operation which does not satisfy the associative law, what should I do inLazy propagation.Hi, I enjoy your post. Just wondering do you have templates for 2-D segment tree as well?
PrinceOfPersia has post about data structures:Link.
And for segment tree:Link.
He is PrinceOfPersia now
He is PrinceOfPersia now.
He is PrinceOfPersia now
Million Dollar question (for everyone AmirMohammad Dehghan) except his future handle will be ???
Who can guess? ;)
N.A.
I solved some questions based on this method (non-recursive segment trees) and it worked like a charm,but I think this method fails when building of tree depends on position of nodes for calculations, i.e. when there is non-combiner functions. Example: https://www.hackerearth.com/problem/algorithm/2-vs-3/
Is it possible to solve this problem using above mentioned method ?
Sure. Non-recursive bottom-top approach changes order of calculations and node visiting only. If that does not matter (and it does not if there are no complex group operations), you can apply all top-bottom tricks, including dependency on node's position. One way is to get node's interval's borders based on its id, another way is to simple 'embed' all necessary information into node inself, so it not only know value modulo 3, but also its length (or which power of 3 we should use when appending that node to the right).
the range modify function is not working can you explain it please ?
void modify(int l, int r, int value) { for (l += n, r += n; l < r; l >>= 1, r >>= 1) { if (l&1) t[l++] += value; if (r&1) t[--r] += value; } }
First thank you for this awesome tutorial.But one thing I was confused about ever since I read the first code was why do you always say :
if (r&1)shouldn't it beif ((r^1)&1)? because if r is odd then we have all of the children of its parent , so we do the changes to its parent rather than r itself.remember that operations are defined as [l, r), so r always refers to the element in the right of your inclusive range.
Yeah. Thx. got it
This blog is brilliant! Can you also add a section on Persistent Segment Tree? We need to create new nodes when updating a node, how can it be done efficiently using this kind of segment tree? Thanks!
Hi, Al.Cash!
Frankly saying, I didn't watch the whole entry. But anyway I want to coin something.
The reason I use recursive implementation of segment trees besides that it is clear and simple is the fact that it is very generic. Many modifications of it come with no cost. For example it is the matter of additional 5-10 lines to make the tree persistent or to make it work on some huge interval like [0;109]. Your tree is heavily based on binary indexation. So, such modifications should be pretty hard. Am I correct?
True, is't impossible to modify this approach to support persistency or arbitrary intervals. However it handles all other cases better and they are the vast majority. Especially it's noticeable in the simplest (and the most common) case.
The choice is up to you, of course :)
BTW you can just use unordered_map instead of array in order to make it work on some huge interval like [0;109]. AFAIK it's well known trick used with Fenwick Tree.
Noooo. Very, very, very bad idea. The constant is too large even for Fenwick. Many problems where [0;109] expect participant to compress the data instead of using dynamic structure, so it is usually hard to get accepted even with fair dynamic tree. Using unordered_map instead of it is simply waste of time, in my opinion.
Yes, you are right, data compression of course better. But I guess that perfomance of BIT + unordered_map is not so much worse than performance of dynamic tree. From another hand it's extremely easy way to modify this data structure and it's also possible for some problems.
I'm not that much into C++, but shouldn't this statement
scanf("%d", t + n + i);be actually:
scanf("%d", t[n + i]); // since t is an array?
Those are equivalent. In the first case C treats t as a pointer.
PS: in the second you would need to write
&t[n+i], that's why the first one is easier.PPS: C/C++ is very crazy,
3["abcd"]works and is equivalent to"abcd"[3], this is shit.I want to update every element E in range L,R with => E = E/f(E); I tried hard but can't write lazy propagation for it. function is LeastPrimeDivisor(E) . Can anybody help me?
Don't answer this question as it belongs to live contest
Is lazy propagation always applicable for a segment tree problem ? Suppose we have to find the lcm of a given range, and there are range update operation of adding a number to the range. Is Lazy propagation applicable here?
No. You should know how to fix the answer without knowing the exact elements in that range.
How do I optimize solution to such problems then? It will TLE for range updates ( no lazy ) for N <= 10^6.
Can you provide the link or the full problem statement?
I would but there is a similar problem in a live running contest, where I have to make range updates to a similar problem. I think i should discuss after the contest ends.
Could you please explain the theory behind the first query function? I get how it works but i don't know how to prove it is always correct. I am doing a dissertation on range queries and i am writing about iterative and recursive segment trees, but i have to prove why these functions are correct and i'm struggling right now.
Thanks in advance.
Under "Modification on interval, single element access", in the query function, why we need to sum up the res? We are asked to give the ans 'What is the value at position p?'. We need to reply a single value, why we are summing multiple values in res?
I didn't understand. Can anyone please explain me?
is it always give the right answer ??
int query(int l, int r) { // sum on interval [l, r)
int res = 0;
for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
}
return res;
}
suppos int array[]={154,382,574,938,827,923,949,748,806,78};
if we build segment tree it will look like this t[1]=6379,t[2]=3117,t[3]=3262,t[4]=2581,t[5]=536,t[6]=1512,t[7]=1750,t[8]=1697,t[9]=884,t[10]=154,t[11]=382,t[12]=574,t[13]=938,t[14]=827,t[15]=923,t[16]=949,t[17]=748,t[18]=806,t[19]=78;
int query(5,8);
answer should be 3426.
but it gives 2620
Right end should not be included into the sum.
For the sake of breaking language barrier, this bottom-up implementation is called “zkw segment tree” in China, because it was (supposedly) independently discovered by Zhang Kunwei in his famous paper. Not sure who was the earliest inventor though.
Is there a way that we could do better for non-commutative segment trees? For this implementation sometimes node are just not being used, as extra merging were done. (eg: for size 13 in the example shown, we merged 2 and 3 even though it is meaningless)
I just wonder if i could make arbitrary size of array to some nearest power of 2 if i put useless values which don't affect to final result of each query to the rest of indices? For example, making a size of array from 13 to 16, or 29 to 32 and putting -inf for the additional indices in a max-segtree(or 0 in a sum-segtree)
Sure you can.
thank you for your reply. But I'm just wondering how people usually implement codes for range operation. For example, fenwick tree with lazy propagation for some situation or non-recursive segment tree(like this article) or recursive segment tree. Which one is the most simple for specific situation? I just heard that it is easier to implement segment tree with lazy propagation with recursive way. So I just wanna know.
Implementing lazy propagation in recursive way is much easier yet less efficient than iterative approach
I would go with Fenwick Tree if it's sum/xor or something similar and with iterative segment tree otherwise unless the update function is hard to implement and debug in time
So you would go Fenwick Tree whenever you have to do range sum/xor stuff even if you need lazy propagation and would go iterative segtree if there is no need of lazy propagation or complicated stuff in operations except for sum/xor and recursive way for the others, right?
Right :D
There is also a trick to do both range queries and lazy range updates with Fenwick tree here
Can you explain how does it handle both of them more clearly?
Here is a good explanation — GeeskForGeeks — Binary Indexed Tree : Range Update and Range Queries
How to find index of segment tree by given sum. example acm.timus.ru 1896
I mean, need find that i, which query(0,i) == sum.
Please, can someone explain apply and build functions in lazy propagation in max queries...?? Really need help there.
Some theory: initial: we have array a[0...n-1] — initial array. t[ 0 ... n + n ] — segment tree array. d[0...n + n ] — lazy propogation array. d[i] = 0 (i=0..n+n-1) initially.
1) t[ i + n ] == a[i], if 0 <= i < n. So if a[i] increments a
value, t[i+n] also increments thevalue.2) t[i] = max(t[i * 2] , t[i * 2 + 1]) , if 0<= i < n. we call t[i] as i-th root of segment tree, because, t[i] = max{ a[ i * 2^k + h — n ], where i*2^k >=n, and 0<=h<2^k } for example, n = 8. so t[3] = max{ a[3*4 — 8], a[3*4 + 1 — 8], a[3*4+2 — 8], a[3*4+3-8]} = max{ a[4], a[5], a[6], a[7] }
3) d[i] = 0, if there not increment operation in the i-th root. d[i] > 0, need increment all of t[i*2^k + h] element by d[i]. see below.
4) if t[i*2] and t[i*2+1] — incremented same
valueso, t[i] — maximum of t[i*2] , t[i*2+1] also incremented tovalue. It's applied recursive.5). if need increment i-th root to
value, by standard algorithm need increment t[i], t[i*2], t[i*2+1], t[i*4], t[i*4+1], t[i*4+2], t[i*4+3], ...., t[i*2^k+h] nodes tovalue. but, with lazy propogation, all these operations absent. Need only increment t[i] and d[i] tovalue`. d[i] > 0 means, t[i*2^k+h] values will incremented some later.GoOd LuCk.
Thank you very much...... Such a great help.... I was really stuck there.
Thanks for yur help. Can you tell how build and push works in sum queries (It says new build and push methods incorporated both types of build and push methods mentioned before). I can't seem to get it. Also why does both calc and apply update t[p]. NO understanding these both methods...
By compacting the code (by author), code longer is simple in understanding although it is simple in implementing....
Which :
1) update: Assignment in range, and query: sum in range ??? OR
2) update: Increment in range, and query : sum in range ??
increment in range query.
This entry explains for Assigment in range, sum in range — and it is difficult than increment operation.
But, If you want increment in range, it simple than assignment.
Let Theory, again; 1<=n<=N ~ 10^5. a[0], a[1], ... , a[n-1] — given array. Need apply two operations:
increment a[L], a[L+1],... a[R-1] to
value, i.e [L..R) range.find sum a[L] + a[L+1] + ... + a[R-1] , i.e. [L..R) range.
t[0..n+n] — segment tree array. d[0..n+n] — lazy propogation.
where
t[i] = a[ i — n], n<=i < n+n. and
t[i] = t[i*2] + t[i*2+1], for 0<=i<n.
If a[i] incremented by
value, so t[i+n] also incremented byvalue.if t[i*2] and t[i*2+1] incremented by
value, they root t[i] incremented2* value. and its applied recursive down.In general, if all
leafnodes of i-th root incremented byvalue, so t[i] should increment thevaluemultiply number ofleafchildren of i-th root.for example: n = 8. if a[4] , a[5], a[6], a[7] increment by 5, so t[12], t[13], t[14], t[15] incremented by 1*5, t[6], and t[7] — incremented by 2*5, and t[3] incremented by 4*5. t[3] — has 4 children.
leafnodes from i-th root of segment tree will increment by d[i], and applied 2.step operation recursivily.For example: if need increment a[4..7] to 5. There only increment t[3] to 5*4, and put d[3] = 5. This
applyoperation. Other nodes t[6], t[7], t[12], t[13], t[14], t[15] nodes will incremented some later (may never).You are great, man!!! Really. Very very much helpful
Last very silly question. What if n is not power of 2. Do we have to first increase n to the nearest power of 2 and fill values with zeroes or there is a way getting around it??
Hmm, Did not test for n != 2^k . There may some bug when calculate children of i-th root, iff n != 2^k, be careful.
In competitive programming, I, always, use n = 2^k.
For example:
Thanks man for all your help. I was stuck here for very long time......
All the codes in the article work for any n.
but for n!=2^n wouldn't there be one entry left which will have parent whose range will be 2 already and on adding this additional child its range become (2+1) ????
Thanks in advance
Could you explain how the query function for this question would be? 380C - Sereja and Brackets I've done it with the recursive approach, but am not able to code the query function using this method.
I too have encountered the same problem.BRCKTS is the easier version of 380C — Sereja and Brackets but how to modify query function according to the problem as t[p>>1] = t[p] + t[p^1] logic will work for only all problems related with associative operations but here it is not.So I solved this problem by changing the logic to t[p]=combine(t[i << 1], tree[i << 1 | 1]) where p goes from (n+p)/2 to 1 in reverse for loop.Anyone has much more easier modification idea please share.
my incorrect solution of that problem: 5684965
how I fixed it: 5685269
Actually in 380C — Sereja and Brackets no update type of query is present so no need of modify function is there which will be easy to do with the above mentioned optimized segment tree implementation. Try this BRCKTS using the same modify function as mentioned by Al.Cash you will realize it will not work in that way.
there are at least 3 ways to solve this problem.
if memory is not an issue then you can just set array length to the power of 2
modify query function: 6026442
split queries: 6006570
I implemented a generic segment tree based on this article: Code. Usage: simply write two structures
struct nodeandstruct node_updaterepresenting your tree nodes and updates, then provide function pointers that merge two nodes together, apply an update to a node, and merge two updates.Example: 27103823
As a noob I am still confused that what is the requirement of modify() function. As you are just doing the same thing that you did in build() function. Please explain.... But I must say you explained the whole concept in a nice manner..
The idea is that modify() runs in O(logn) so doing it for every point is O(nlogn). build(), on the other hand, does the same thing but runs only in O(n).
This might not be significant in simple cases but will make a difference for complicated operations, or when num_queries < n.
noob here, Say the input is of size 6
Following parent child relationships are made:
If the usage context is such that the rules are different for processing left and right childs, then we will have wrong result, since node 2 should ideally be processed as a right child .
e.g. http://www.spoj.com/problems/BRCKTS/
I have been testing other sizes that incur in the same problem, as size 7 or 5. I do also agree that in these cases, if the operations is not conmutative or handles differently left and right children, this implementation will give an incorrect answer. Can you clarify Al.Cash?
EDIT: Autocorrection: Those nodes are not used in the queries.
Can somebody please explain what the bitwise operators do here cause its very difficult to catch up?
P.S — I know about Bitwise operators but have never used them in my code.
Thanks.
If p is a node in the tree, then
p >> 1is its parent,p >> sis its sth ancestor,p << 1is its left child, andp << 1 | 1is its right child.Thank you soo much!!!
Is Binary Search possible like classic Segmented Tree ?
int ask(int id, int ID, int k, int l = 0,int r = n){// id is the index of the node after l-1-th update (or ir) and ID will be its index after r-th update if(r — l < 2) return l; int mid = (l+r)/2; if(s[L[ID]] — s[L[id]] >= k)// answer is in the left child's interval return ask(L[id], L[ID], k, l, mid); else return ask(R[id], R[ID], k — (s[L[ID]] — s[L[id]] ), mid, r);// there are already s[L[ID]] — s[L[id]] 1s in the left child's interval }
http://codeforces.com/blog/entry/15890
If n is a power of 2, than you can use the identical code as in the classic recursive Segment Tree.
If n is not a power of 2, it is still possible, but it is definitely harder.
One possible approach: - collect all indices of the segements that partition the query segment (be careful here, the iterative version alternatively finds such segments from the left and right border): there are O(log n) many - then iterate over them from the most left segment to the most right one, until you find the segment that contains the element you want to find. - then continue traversing to either the left or right child until you reach the leave node (this can be done iteratively or recursively).
I have a question about this part of the code on the section: Modification on interval, single element access
int query(int p) { int res = 0; for (p += n; p > 0; p >>= 1) res += t[p]; return res; }
Why do we travel all the way up the tree? Why do we not just return t[p+n]? I think I am missing something.
Edit: It's prefix sums.
I wrote some notes for query function, might be useful to others
I've modified the code lazy propagation for sum queries (Increment modifications), but it isn't working. What's the problem?
https://ideone.com/TQsEjs
When you increment the interval by a value, you need to add this value times the interval length to the sum. So, you need to modify the last example where the interval length is maintained, not the one you took.
ok, thanks!
Hi,
I also have some issue with this. The code in the link looks perfectly fine to me, even though it may not be working...
Edit 2.: Task using below code was accepted, so there is a chance that below procedures are correct for range increment and sum queries.
http://codeforces.com/problemset/problem/914/D — Can non-recursive segtree be used for this problem ?
Yes : http://codeforces.com/contest/914/submission/34679495
Thanks for writing!I think this blog very useful for everyone,especially people who want to study about segment tree.Segment tree is a data structure that very amazing and great.This blog give me more knowledge about segment tree
Could anybody share a 2d implementation of this segtree? Specifically, I'm trying to solve http://www.spoj.com/problems/MATSUM/ with it, but can't get it right :c
Thanks you for awesome post! Do you mind if I translate this post into Korean and share it on my blog? Of course I will cite this page and make sure that you are the original writer.
Sure, no problem.
[sorry, i was asking a stupid question, i got the answer myself]
For the first code snippet, why does this not work ? The only thing I changed is I wanted L, R to be inclusive. If R is even which means its the left child meaning it should be added and moved left and iterate over its parents.
Try calling
sumRange(1, 1). What happens?You must do
l <= rinstead ofl < r.Is it possible to do Binary Search on this kind of Segment Tree?
This write-up is amazing. I come back to this every year and learn something new.
Read this(seg_tree_blog) after this(for me).
Hi Al.cash , after watching few tutorial videos and understanding segment tree, I tried to implement it by understanding your tutorial. I never knew I would be able to implement it so quickly and so efficiently. I can't thank you enough for providing this tutorial. Thankyou so much!!
As mentioned, the push function takes O(log(n) + |r - l|) time to complete and it is called on every call to modify(). isn't O(|r — l|) = O(n) which makes push take O(n) time in worst case?
Why doesnt it work for gcd?
https://cses.fi/problemset/task/1190/ Can someone solve this question?
I have tried to solved it. It is giving correct answer for small values but it is giving wrong answer for large values. Here is my solution. https://ide.geeksforgeeks.org/XMbjHTJeEQ
Thanks :)
Problem Statement says, "Empty subarrays are allowed".
So, I guess, you're printing $$$-10^{17}$$$ in case you should print $$$0$$$. Just initialize everything in query to $$$0$$$, instead of $$$inf$$$.
https://ideone.com/W2obub It is still giving WA. :(
Okay, so I implemented it on my own and now I know where the problem is.
During implementation, I was stuck at query function. I asked myself, from which side do I want to combine the left and the right values. This is the problem. ( AI has explained it under the section "Non-commutative combiner functions" ).
We need to keep two answers. One from the left (lans ), and for each l-type ( fancy term for if(l&1) case ) node, merge lans with l ( order matters ). And for each r-type, merge r with rans.
Finally merge lans and rans. Code here
Also, thanks to your query, I have learned something new today ( which hopefully I won't ever forget ). So, thanks a lot. And ofcourse, Al.Cash thanks to you too for so many helpful blogs.
Thanks a lot! :)))))
I am not sure but I think a short correction is needed when query is made with right border.
May be it should be like:
instead of
Read this comment
Can someone plz. provide me with an implementation for binary search in this kind of seg tree, coz. now i am really hooked to this style. BTW what i want to do is like find the first element which is greater or equal than some k(queries) using seg tree coz. there can be updates in the array. I am not able to do it for n which are not powers of 2. Thanks in advance any help will be appreciated.
with the case :
the modify and query functions are :
.
Read the tutorial examples carefully. [r, l] and [r, l) -- see any difference?
.
Come on, just sit and iterate your algorithm manually and see what goes wrong. It will not do any good to you if you just use the code without understanding how it works.
Note that there are sometimes reasons to round up the tree size to the nearest power of 2. This uses more memory, but forces the shape into the "perfect binary tree" which makes some operations possible/easier, like unconditional $$$O(1)$$$ access to the root (especially useful if the combining op is expensive), or in-place binary search in $$$O(\log n)$$$. Not to mention also somewhat simplifying the tree structure for relative beginners who need to make sure their lazy propagation or other modification works right.
I totally agree. It's a good example for "a coin has two sides". We can't say that which one is better.
Sorry, but I think tradition/recursive implementation is much much simpler and easy to understand(at least for me) and also is less prone to mistakes. It's Just what I felt after reading traditional implementation after this one. Though I must say its really interesting and well-written blog.
.
Is it possible to find kth-order statistics in the problem 1354D - Multiset using the non-recursive implementation of segment trees mentioned in this blog in which the array is arbitrarily sized(i.e the segment tree array size is not some power of 2).
use fenwik tree it is standard ques https://codeforces.com/contest/1354/submission/80799964
Yes I did actually previously solved it using Fenwick tree. But recently I was learning about the non-recursive segment tree and so to practice I thought of solving the same problem using it. But I was unable to code for finding the kth-order statistics using the non-recursive approach of segment trees.
search "seg tree question codeforces" on google you will find a great blog which have very good practice queue on seg tree
can you plz share your seg tree approach if you got solved!!
Here. Just find and store all the roots when initializing.
Can anyone explain this part "scanf("%d", t + n + i)"? where does scanned element get stored?
It will be stored in array with name t, at location n+i
Is it possible to do a range sum update and make a range product query?
Can someone help me, I try my best but cant solve this problem using Iterative Implemenetation
The problem
Modification on interval, single element accessI can't understand how these functions are working and I try to implement them on an array and it is giving wrong output can anyone plz check it
an example where it failed
array = 3 2 1 2 now after build, the tree should look like this 0 8 5 3 3 2 1 2
now we will modify range 0 — 1 inclusive and add value 1 so after this, the tree looked like this 0 8 6 3 3 2 1 2
now if we query the 0 indexed element output is 17 whereas it should be 3
Here's a quick implementation you can compare with.
thanx for showing that cool struct. The update function in that struct works for a particular index type query whereas I have doubt in the modification in interval type query. Sorry if I was misunderstood something.
It does range addition and point queries. I can wrap that up in the struct as well. But the segment tree is actually the difference array. Just input $$$n$$$, then $$$A_1, A_2 \dots A_n$$$, then $$$q$$$, then $$$q$$$ lines of $$$l r v$$$, where it adds $$$v$$$ to the indexes $$$i$$$ such that $$$l\le i \le r$$$.
Hello, I was wondering how would you convert the following into querying for minimum? I've tried substituting the logic in the loop but was getting some weird answer. Thanks
EDIT: I figured it out forgot to change build() as well.
Is there any way to convert this iterative segment tree into querying the number of minimums within the range?
Thanks in advance!
You can store pairs instead of numbers, so the first element will store the value, and the second the count. When merging nodes, compare for the first of the pair: If they are equal, sum the second elements. If not, just keep the node with smaller first.
Init is t[i+n] = {a[i], 1}, for i=0,...n-1
Hi. For the range modification and range quesry shouldn't it be
if (!(r&1)) res += st[r--]I am confused as to how your approach works, since I used it for a submission in a problem and it didn't pass, while the one I mentioned above did. Can u pls explain?Everything he has written, was for half open interval $$$[l,r)$$$, and in particular, changing
--rtor--will not always work. When you query for a range $$$[l,r]$$$ just put the parameters in the function as $$$(l,r+1)$$$.Hi. Could you please tell how would the code you have provided be modified for the problem of "Count elements which divide all numbers in range L-R"?
You can make a tree for gcd and a tree for min (with count). If the min of the interval is equal to the gcd, nice, the count of the mins is your answer. Otherwise is 0.
This is because the required numbers should divide the gcd of all the elements in the interval, but at the same time are elements, so just the minimum could be a value to count
given an array of n elements, and q queries with two types 1 l r s e indicates flip bits of positions [s,s+1,....e] of subarray [al,..ar], 2 l r s e indicates print the number of set bits [s,s+1,...e] of subarray [al,...ar] n<=q<= 10^5, a[i] < 10^9 0<s<e<30
Can anyone help me in doing this?
Great Tutorial !!!
What is the difference between these two
modifymethodsCode 1-
Code 2-
Why
code 1cannot keep the order of the children and we needcode 2to keep the order to usecombine(...)method ?There is no big different when you compare their modify function, the most important different is when you do non-commutative query, you should keep two empty node(let's call it left/right node), and during the query, if t[l] need to be combine, you should combine it to left node, when t[r] need to be combine, you should combine it to right node, and combine left node and right node in the end.
Thanks for explaining it. Can
code 1changed as below to keep order —Actually both code1 and code2 keep their order.The reason why author use combine() instead of + in code2 is to convey that the data we want to maintain is no longer commutative(unlike"+" operation).
If I have only 3 elements, t[1] should be combine(t[3], t[2]), but I think this algorithms does combine(t[2], t[3]), If I'm not mistaken I think it doesn't work on non-perfect binary tree
Same goes for modifying function
If you only have 3 element in your segment tree, t[1] will be useless because element 1 will be stored in t[3], element 2 in t[4], element 3 in t[5].
when you do query/modify on this segment tree, you will only use t[2], t[3], t[4], t[5].
If I want to make tree node can take 4 values {suffix,prefix,sum,segment maximum sum}.
How can I build or modify tree by this non recursive method??Al.Cash
Thanks Al.Cash for the awesome version of segment tree. Once you understand it, it really is super simple! Far better than recursive.
Easier version for beginner to read( i don't think so...)
thanks man
Is it possible to implement functions such as Finding subsegments with the maximal sum with this implementation?
Hello,
Thanks for the wonderful post!
Beside saving memory, did anyone compare real speed (not BigO) of "range query" and "range update" with "lazy propagation" between this bottom-up and the classical top-down?
From the code with extra calls push() (aka. pushDown) and build() (aka. popUp), I guess that the bottom-up is 3x slower than the top-down solution, right?
What are the limitations of the bottom-up solution you experienced so far?
Not sure why people down vote my questions? I am sorry if my questions are stupid. I would like to understand the down vote reasons so I could improve my communication with this community. I saw that a previous comment, just saying "Great Tutorial !!!" got -28 down votes. What's going on here?
To be emphasized, I am asking only about the "lazy propagation" version. The simple version without it, is for sure faster than top-down solution.
The push function if called with a range of 1 doesn't need the r variable, so one can create a push1 function (which only pushes 1 element). It actually provided me with a 2x speedup in 1440E - Greedy Shopping.