** UPD: Formulas are already fixed. **
163A - Substring and Subsequence
Solution summary: dynamic programming.
Sample jury solution: 1415300 (author = levlam)
The problem could be solved with the following dynamic programming. Let f[i, j] be the number of distinct pairs ("substring starting at position i" and "subsequence of the substring t[j... |t|]")
Then:
f[i, j] = f[i, j + 1];
if (s[i] == t[j])
add(f[i, j], f[i + 1, j + 1] + 1)
Answer = 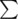 f[i,0]
f[i,0]
Solution summary: sorting + binary search.
Sample jury solution: 1415306 (author: Burunduk1)
We need to find the minimal time T. Let us find it using binary search.
Once the time is fixed, one can arrange lemmings using greedy approach starting either from the top or from the bottom. In this solution we consider the way to start from the bottom. Among all lemmings, that can get on the first ledge, let's choose the lemming with the minimal weight (and among all such lemmings the one with the minimal speed). Why is it correct? Assume that we used some heavier lemming, then we can't use any lighter lemming anywhere, so we could replace it. Among all lemmings with the minimal weight we choose the slowest, as the faster ones can climb higher.
To arrange lemmings fast, we can sort them beforehand, comparing first the weight and then the speed. After if, we consider all the lemmings in that order and either choose the current one, if it can get in time, or leave it. It is useless to consider one lemming twice, as we won't be able to use it anyway.
So, the solution consists of sorting and a binary search with a linear search inside. The time is  .
.
However, that was not enough. One also had to deal with precision problems. Let us evaluate the number of binary search iterations.
0 ≤ T ≤ H * K (the maximal time does not exceed 109). We need to understand how the times can differ. In the case of "N = K = 105, H = 104, V about 109" the times needed for two lemmings to get on some ledges, can differ by 10 - 18, as the times are fractions like 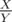 , where X and Y are about 109.
, where X and Y are about 109.
So we need to make log21027 = 90 iterations. In fact, jury solution made 75 and that was enough, however 70 was not. The idea above shows that 90 will be definitely enough.
Solution summary: events along the circle or binary search.
Sample solution: 1415310 (author: Burunduk1)
Sample solution: 1415316 (author: arseny30)
Wherever Anton starts, he will run along the conveyor a segment of length 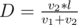 . Consider one candy. To eat it, he needs to get on the conveyor in any moment of the segment [ai - D..ai]. Consider all points like ai - D and ai (add 2l if that is negative). Also add points 0 and 2l.
. Consider one candy. To eat it, he needs to get on the conveyor in any moment of the segment [ai - D..ai]. Consider all points like ai - D and ai (add 2l if that is negative). Also add points 0 and 2l.
Sort these points. Consider two neighboring points: x[i] и x[i+1]. If Anton starts at any moment between them, he will eat the same amount of candies.
From now on, we can create one of the solving solutions:
Start from every middle of the segment M = (x[i]+x[i+1]) / 2 and use binary search to find the number of candies on the segment [M..M + D].
Consider events along a circle like (a[i] — D, +1) and (a[i], -1). One needs to move twice along the circle and use the second run to add the current length to the answer for the current number of candies.
The both solutions require 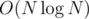 time.
time.
Solution summary: backtracking + boundaries evalutaion.
Sample solution: 1415320 (author: Burunduk1)
The solution consists of three main ideas:
V = ABC, A ≤ B ≤ C тогда A ≤ N1 / 3, B ≤ (N / A)1 / 2.
A and B are divisors of V, as we are already given the factorization of V, we can run only through the divisors
Given fixed A, the optimal real B and C are (N / A)1 / 2 (denote this values as X). I.e. the square will always be greater than ≥ 2(2AX + X2). So we can use this value as a boundary for the answer.
If that still was not enough, one could optimize using the following ideas:
Border evaluation will be more useful while running through possible values of A in descending order
A and B are 32-bit integers.
Once we have calculated the answer for V, memoize it (this one makes possible maximal test a bit smaller).
If anyone needs any theoretical base, here's some statistical information:
The maximal number of divisors of numbers from 1 through 1018 is 103860 (the number 897612484786617600 = 2834527211 ...)
Using only first two optimizations, the number of numbers A, found by our solution, is 10 471 (in the case of the number with maximal number of divisors)
Using only first two optimizations, the number of pairs of A and B, found by our solution, is 128 264 (in the case of the number with maximal number of divisors)
Solution summary: Aho-Corasick and finding the sum along a way in a tree of suffix links
Sample solution: 1415345 (author: arseny30)
We assume that the reader is familiar with the Aho-Corasick algorithm (http://en.wikipedia.org/wiki/Aho-Corasick)
Consider a trie of names and suffix links over it. For every vertex v one can calculate the number of names, ending in that vertex (end[v]).
Then, the "add name i" operation is end[v[i]] += 1, where v[i] is ending vertex of i-th name.
Similarly, "remove name i": end[v[i]] -= 1.
To answer a request "calculate how politicized the text is", one needs to know, that the suffix links form a tree. Once we move though the text and simultaneously through the trie with suffix links, we add the sum of all end[v[i]] along the path to the root of the tree of suffix links the politicization of the text.
Now, there's another problem: we need to calculate the sum of weights along a way to the root, the weights may change.
One can do it in the following way:
Move the weights from vertices to corresponding edges to vertices' parents
Build the Eulerian traversal of the tree, where the down-move will store positive weight of the edge and up-move will store its negation.
The sum along a path to the root if the sum on a segment of the Eulerian traversal (the endpoints are any entries of the vertices in the traversal).
A fast and short way to calculate the sum on a segment is Fenwick's tree.
Here's a solution running in O(|SumLen| * log) time and 26 * |SumLen| memory (the trie will not be compressed).











Thanks for the editorial. Please provide an English edition. Meanwhile I noticed that the author's submissions aren't accessible at this moment.
I'll give access to the solutions soon.
Fixed
In problem B " So we need to make log (10^27) = 90 iterations " where from 10^27 came ?.....i just want to know how you concluded that 75 iterations will be enough.
You have a range of doubles [0, 1e9] and two doubles here are considered "equal" if their substraction is less than 1e-18. Then you actually have 1e27 "different" double values, don't you?
please help!! i tried to submit my solution to the problem E many times, but my solution couldn't be received. the screen says "Ooops! Something has broken down in Codeforces. Do not panic, you can try to reload the page or return Home. Anyway we will carefully read megabytes of logs, analyze stacktraces and fix the problem.". i tried submitting a empty-code to it,and the code was received(of course, wrong answer). and i tried log-out and log-in,but the situation didn't improve. ??why?? my code is no compile-error, or memory limit exeed. also, i tried the custom test,and the custom test was no problem.
thank you for fixing the problem ^_^ my cause of trouble is using the "%lld". now,the program doesn't be received,too,however,the screen told me a proper warning.
Could someone explain me, why mathematicaly 90 iterations is enough for 163B — Lemmings? I have done a solution with 40
can someone please elaborate the dp states and transition of A.
In problem 163A - Подстрока и подпоследовательность, should the formula for
Answerbe the summation overioff[i,|t|]instead off[i,0]? 39291217Update: The answer is NO! The editorial code reverses the direction of the
jloop, and the original formula is correct.