Very interesting contest.
But, how to solve task L, G and J?
Thanks in advance.
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Very interesting contest.
But, how to solve task L, G and J?
Thanks in advance.
| Name |
|---|



L: For each color check all cells in its bounding box. It will work in O(n3), because if bounding box has dimensions w and h, then there should be at least w + h - 1 cells of this color.
J: Run 1 iteration of Boruvka's algorithm.
It seems that the tests are too weak.
An O(n3logn) solution with BIT can pass problem L and an O(mlogm) solution using Kruskal can pass problem J.
I got O(n3log4(n) accepted...
That should be logarithm overflow.
I've got TLE with my O(n^3) solution :/
We solved problem L with O(N^3) complexity and got TLE!
Maybe someone can explain L more verbosely? I can't understand neither aid nor witua's team explanations :(
I didn't realized how to solve cases
Suppose that n = m for simplicity.We want to prove that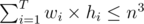 . We have that
. We have that 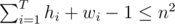 (as explained above), multiply both sides by n and obtain that
(as explained above), multiply both sides by n and obtain that  .
.
You can also approach it from the other end — instead of trying to find all boxes contained inside this box, you may try to find all boxes which contain given box.
Just pick any row which intersects with our box and check all colors presented in this row — there will be O(n) of them, and clearly any valid box containing our box should have at least one cell in this row, because of connectivity.
P.S. We had to optimize it a little bit (like "let's only check boxes which have area larger or equal than area of our box") because initially it gave TL.
I didn't realize there is an easy solution in L and solved it in O(n2) time similarly to this problem
Can you please elaborate how you do it in O(n2)? It's not clear to me even after reading the hackerrank editorial...
For each component choose some point to be its' representative. Now consider some bounding box b. Calculate amount of representatives inside it with prefix sums in O(1). Some components were added to the answer incorrectly, some components were not added to the answer, but should be. Both of them going through the border of b so can be handled in O(h(b) + w(b)).
Oh, so this is O(n2)? That's what we did during the content, but we thought it is O(n3). Actually makes sense, number of cells in a connected component is at least len(border) / 4, and I see a similar explanation in the thread-starting comment. Thanks!
G: We can take size of each pile module A + B.
It's obviously correct when second player wins smaller game (make turn to the same pile as first player it's possible, or use his strategy in smaller game otherwise). First player makes first move as in smaller game and becomes second.
Only one player can make a move on the one pile, because size of pile < A + B. Then both players should always choose the biggest pile, so we can just iterate the process.
How to solve The Most Expensive Gift?
Our solution was to check all possible cycles of length <= 6. And it got AC. I am not sure if it is right.
At least one of the characters has to be present times. So we definitely have some subsequence with score
times. So we definitely have some subsequence with score 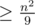 . So checking all cycles up to 9 definitely works. We didn't reduce the bound any further as this was enough to pass.
. So checking all cycles up to 9 definitely works. We didn't reduce the bound any further as this was enough to pass.
Oh. Really easy proof!
Hm. One can proof why we can check all periods of length <= 9. Because due to the Dirichlet principle one letter will occur ≥ N / 3 times. So, using one letter we can reach answer N2 / 9.
The numerator of the fraction is always < = N2, so to reach better answer, we should have smaller denominator. So, the length of the period shuld be < = 9.
UPD: late
For example if S =
("ab" + "c" * 5 + "ab") * 2, then( length(ab) * count(ab) ) ^ 2 / length(ab) = ( 2 * 4 ) ^ 2 / 2 =32 and( length(abcccccab) * count(abcccccab) ) ^ 2 / length(abcccccab) = ( 9 * 2 ) ^ 2 / 9 =36Just take cycle = "c". Answer will be 100
You are right, then instead of 'ccccc' -> 'cdefg'.
You don't have defg in your alphabet.
Ah, ok. My bad. I haven't solved this problem and later forgot about a size of alphabet.
Actually, c<=6 is correct bound.
Let k be the number of times cycle of length c appears in the string. So its score is c·k2. On the other case some letter appears at least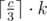 times. Solving inequality
times. Solving inequality 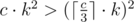 gives c ≤ 6.
gives c ≤ 6.
Lost 20 minutes on E thinking why TC #4 is going to be correct but not Error :D But later realised that Error can be correct.
How to solve I?
Count occurrences of
"1"in each line and each row. Then goup->down, and laterleft->right, and try to cut pie. After you cut it inton^2pieces, check every peace if it has exactly 1"1".(UPD: somehow Div.2 I is not same as in Div.1 but corresponds to D)
It seems we never need to take balls from three different boxes. Does anyone have a proof?
I’m not sure it’s ok, but I believe there is an equivalent problem, where after you get a ball, you remove all balls with the same color, and the game ends when there are some empty set of boxes which initially had at least 2 balls of some color. This is a state game, where the state is the mask of balls that you removed. And all the final states can be covered by states where you emptied one or two boxes (and possibly some other along the way, but they are irellevant). There is only one minimax path along this graph, and it will always end up in some state where you emptied one or two boxes. Now, supposing that you have infinite computing power and you find the optimal final state to converge to, you can then apply the strategy to only clear those boxes.
It should probably be
because it's possible there are no duplicates in boxes at all.
How to solve H? I got WA 41
How to solve C?
You may want to check out our short descriptions of the solutions.
Explain, please, how to participate Grand Prix of Ukraine ???
How can I upsolve the contest?
Where can I find the problemset?