Tutorial is loading...
Solution By: Bingheng Jiang (NOIRP)
PS: The characters in problem 894A is Diamond and Bort from Land of the Lustrous.
Tutorial is loading...
Solution By: ZeRui Cheng (Marco_L_T)
Tutorial is loading...
Solution By: Bingheng Jiang (NOIRP)
Tutorial is loading...
Solution By: Bingheng Jiang (NOIRP)
Tutorial is loading...
Solution By: Yiming Feng (whfym)
Hope you had fun in this contest and got high rating!
See you next time!











Thanks for light speed editorial and system test :)
Our pleasure :)
Maybe it is because there are not many submissions to test? Therefore, the system test is very fast?
Hope you had fun with this contest and get high rating! See you next time!
Hi! Problem A has an O(n^3) solution, where n is the size of the input string. I was working out the DP solution for the same, but I am getting wrong answers. It'll be a great help if you please post a DP solution as well, please?
Thanks a lot! :D
You can look up a DP solution in contest status.
I opened about 40-45 solutions, all of them are brute-force (including mine) and including people in red color. Looks very less number of people have written the DP solution.
I understand that it's pointless when the bound is <= 100, but this (or similar) question might come up as C-D with higher bounds. If not the whole code, is it possible to get only the psuedocode, please?
But it is not hard to solve this problem in O(n) XD
O(n) solution
What is this -> \t{1}?? Mathematical Processing error or anything else?
emmm... it means 1 the \t{} maybe a processing error?
Sorry it's my mistake. And I have fixed it now.
Hats off to codeforces! Really showed the class today. Whether it be the Amazing tricky Questions or the bullet like speed of system test! Everything was just amazing today.
Can you sort of give me a proof or an intuitive example why the lowest element must always divide all the elements in the set?
UPD I mean i understand why the answer will always be what it is whenever the smallest element divides all but i guess what i'm really asking is how to come up with such a solution. My bad I guess I need to improve my skills a lot.
Use the GCD of all the numbers to divide all the elements in the set. Then GCD of the range which includes that GCD number will be GCD of all numbers.
The statement says that all the gcds are in the set, alright? So, the gcd of ALL the elements of the answer must be in the set.
Besides that, gcd(a, b) <= min(a, b), so the gcd of all of the elements of the answer must be the smallest number in the set, so every number must divide it.
(PS: I tried to explain my intuition on it, hope it helps! o/)
Yes this surely helps :). Thank You very much. Like a lot of the participants today I too had misunderstood the question.
However I had thought some parts of what you are trying to explain over here. (Ex- All the elements must be in the set). But the thing is i dont know if I'd be able to solve it or not during the contest. Guess one never knows whether he/she would be able to solve a particular question or not without participating.
Thanks a lot though! :)
I'm sorry, but I still don't understand something: why the gcd of all numbers in the set must divide all the others gcd's? I think that there's something that may be obvious, but i'm not seeing it :(
thanks in advance!
Let's call the gcd of all numbers (sequence [0,n-1] of the answer) x, ok? We know x divides all the numbers in the answer, because it's the gcd of all numbers in the answer.
Now, choose any pair of indexes i and j. x divides all numbers in [i,j], so the gcd of the sequence [i,j] must be a multiple of x.
It helped me a lot, too. Thanks :)
so the gcd of the sequence [i,j] must be a multiple of x.Wait, that isn't obvious. If x divides A and y also divides A, then it is not true that x divides y.
Actually the proof of the statement EdsonSousa was asking for is this: X divides all numbers in in [i,j]. OK. Now, the gcd of [i,j], lets say k, must be greater or equal to x, since if not, x is a better candidate for gcd than k. Now k>=x. Assume now that x does not divide k. This implies that there are some prime factors in x that are not in k (again by contradiction). Since these prime factors divide all the elements of the array, they also divide each element of [i,j]. This implies that multiplying k with these prime factors still makes it a common divisor, and now a multiple of x too.
Hence k is a multiple of x.
Even editorial strongly disagrees with this clarification I got in-contest... Hope it doesn't happen again...
http://codeforces.com/blog/entry/55858#comment-396071
I'm sorry :( Maybe someone replied you in a hurry and made a mistake. You know there were a lot of questions at that time.
Btw, Sharon,Your submission for A and this is too similar.
It's exactly the same method.
The contest was fun..... Thanks for such a great contest!!!!!
Is there a solution for D that works for arbitrary trees instead of (almost) complete binary trees?
Edit: Solved.
In problem B, why If k equals to -1 and the parity of n and m differ, the answer is obviously 0?
suppose that n is even and m is odd. if an answer exists then we have even rows each with odd -1s (even -1 in total) and odd columns each with odd -1s (odd -1 in total) => contradiction
Thanks
Sorry, what does mean [] in 2[(n - 1) * (m - 1)]?
oh, got it. It means 2^((n — 1) * (m — 1))
plz someone explane about "C" . I couldn't understand what I do
if gcd of all set is not smallest element in set — answer is -1; else input: 4 2 4 6 12 output 2 4 2 6 2 12. U insert the smallest element between every two.
Hope i got all correctly
here What is "S"??
S contains all of GCD?????
yes, it contains all gcd for all subarrays
For 894B — Ralph And His Magic Field: if we have case with non 0 answer, why is it that for all possible (n-1) lines and (m-1) columns filled area the uniquely determined solution will not have conflict in [n][m] cell (bottom right)? Why can't it happens that for our right column number of -1 (elements [1][m] to [n-1][m]) will differ in parity from number of -1 in bottom row (elements [n][1] to [n][m-1])?
!Not true, see updated post!
Oh, nevermind, i think I got it. If k == 1, every -1 in row or column should be balanced out by odd number of -1s. So, that means that number of -1s in last row (without [n][m] element) should have same parity as number of -1s in last row (without [n][m] element). For k == 1, same can be said for number of 1 elements. And given that we know that n%2 == m%2, same can be said for number of -1s. Please correct me if I'm wrong
Sorry, my previous post was not a valid proof. I think this one is, though
In case of k == 1 if we have -1 in some cell in last row, let's say it's cell[n][x], for cells in that column x (cells from [1][x] to [m-1][x]) we we can say that there is odd number of -1, because their product should be -1.
If we have 1 in same cell, we can say that number of -1 is even for that column, because their product should be -1.
If we have -1 in some cell in last column, let's say it's cell [x][m], for cells in that row x (cells from [x][1] to [x][m-1]) we can say that there is odd number of -1, because their product should be -1.
If we have 1 in same cell, we can say that number of -1 is even for that column, because their product should be -1.
Let's say there is P -1 in (n-1)(m-1) filled area
Let's say we have x1 -1 elements in last column (without [n][m] element). Let's calculate parity of number of -1 in (n-1)x(m-1) filled area. Sum of -1 in all rows ending (ending meaning [i][m] element is -1) with 1 will be even (sum of whatever number of even numbers is even). Sum of -1 in all rows ending with -1 will depend on x1. For every such row there is odd number of -1. If a1 is even (sum of even number of odd numbers is even), if a1 is odd, sum is odd (sum of odd number of odd numbers is odd). So, we can say that x1= P (mod 2).
For last row (without [n][m] element), let's say we have x2 -1 elements. Using same logic as above, we'll discover that x2 = P(mod 2), giving us that x1 = x2(mod 2). (parity is same)
Therefore, we won't have any conflicts in [n][m] cell.
We'll apply almost similar logic to k == -1 case.
In case of k == -1, if we have -1 in some cell in last row, let's say it's cell[n][x], for cells in that column x (cells from [1][x] to [m-1][x]) we we can say that there is even number of -1, because their product should be -1.
If we have 1 in same cell, we can say that number of -1 is odd for that column, because their product should be -1.
If we have -1 in some cell in last column, let's say it's cell [x][m], for cells in that row x (cells from [x][1] to [x][m-1]) we can say that there is even number of -1, because their product should be -1.
If we have 1 in same cell, we can say that number of -1 is odd for that column, because their product should be -1.
We can do the same as we did before, but this time we'll prove that y1 = y2(mode 2), where y1 and y2 are number of 1 elements in last row / column (not number of -1 elements, as before).
B we already know that for k == -1 case, n = m (mod 2). Therefore, x1 =x2 (mode2), where x1 and x2 are number of -1 elements in last row/column (parity is same)
Therefore, we won't have any conflicts in [n][m] cell
in problem B, why "if k equals to -1 and the parity of n and m differ, the answer is obviously 0"?
If n is even and k = - 1, then the product of all the elements in the grid is the product of all the rows, which is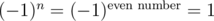 .
.
If m is odd and k = - 1, then the product of all the elements in the grid is the product of all the columns, which is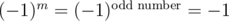 .
.
So n cannot be even if m is odd. Similarly, m cannot be even when n is odd. So m and n must have the same parity when k = - 1.
I still don't get it at all! Not all numbers have to be -1.
suppose k=-1,the product of all n*m elements can be (-1)^(n) = (-1)^(m), so if n is even , the left result is 1, so m must be even as n, so as to get 1 in result; when n is odd , the left result is -1, so m must be odd too. In total, n must have the same parity as m, when k == -1. when k ==1, you can derive the conclusion in similary supposition
Still don't understand ((
now understand. the product of the columns must be equal to the product of the lines. but 1 != -1 so its impossible.
or number of -1's will differ (link comment)
In problem 894B, how will you find 2^((m-1)*(n-1))? I mean the expression (m-1)*(n-1) can even be greater than a 64-bit integer.
By Fermat's Little Theorem, 2(109 + 6) ≡ 20 (mod (109 + 7)). So you can find a and b less than (109 + 7) with m - 1 ≡ a (mod 109 + 6), n - 1 ≡ b (mod 109 + 6) and use Fast Exponentiation to find 2ab.
Hi ntfoim, in your submission why do you add up INF-1 to m and n?
In the case when N = INF - 1, (Nmod(INF - 1)) - 1 = - 1, which can screw everything up in the exponentiation (because my fast exponentiation doesn't support negative numbers). Adding INF-1 after taking mod was just my way of fixing this issue.
We know that:
2(m - 1) * (n - 1) = (2m - 1)n - 1
So first you can solve x: = 2m - 1 mod 1e9 + 7
Then the answer is xn - 1 mod 1e9 + 7
you could also use __int128
Can someone give a more detail explanation of D's solution?
Is there a DP solution for QAQ?
Yes, 32477025. Basically
dp[i][j]is the number of subsequences oft[0..j]ins[0..i]. And to save memory you can get rid of one dimension.it's my opinion, for problem D, time limit is not enough, it's my ac solution after contest http://codeforces.com/contest/894/submission/32482217, it's my my TLE solution during contest http://codeforces.com/contest/894/submission/32473208, both are (n + m) * log2(n) * log2(n), but only one difference is scanf, printf, instead of cin, cout, WHY?
It's common problem that
iostreamis not fast enough for reading 1000000 numbers. You could use the following lines in the beginning of yourmain():And it will become fast.
Author's solution is O(nlogn+mlog^2n) using merge sort.Your solution isn't the intended one,and that's why your solution can't fit in the time limit.
For problem D, Why is it O(n(log(n))^2) for using std::sort? I thought that std::sort was implemented as introsort, which is O(n(log(n)))?
Also, would std::stable_sort be better for this problem since it (given enough space) defaults to mergesort.
std::sorttakesO(n log(n))time. In the editorial they meant that the construction of the complete tree takesO(n log(n)^2)time.Thanks for the clarification
in problem D how do we take into account the nodes not in its subtree?
For each query we go up to the root. So, we change v from a to 1 (excluding) with a = a / 2. Then for each v we take its parent p and p's other child u (if it exists). We could easily take p into account and then take all u's subtree using precalculated data. Note that each vertex belongs to its subtree in this solution.
I wonder in D why my (n*log2(2000000)+m*log2(2000000)*log2(1000000)) is getting tle. http://codeforces.com/contest/894/submission/32482922 I have made a test case where n=1000000,m=100000,it runs successfully.I am using persistent segment tree. I think at least 10^8 operations can be done within 1 second on compiler,so my codes complexity is enough for 2.5 second.If anyone has a explanation where is my mistake,it will be helpful
The logarithm of segment tree usually has relatively big constant C (maybe because of many divisions and random array access). 1e5 * log(1e5) * log(2e5) * C could easily TLE.
Thank u so much
Still I am a bit confuse,how Should I calculate the complexity when there is a segment tree involved .To get TLE the constant factor must be at least 4.
Dunno. You could just try to test some trivial task (e.g. RMQ) with segment tree and watch for how big the constant is compared to some faster (e.g. fenwick tree).
(e.g. fenwick tree).
Perosnally I assume that for most tasks (nmax ≥ 100000) segment tree is slow enough to TLE if there is something like
Could you please explain this line a bit more in problem D?
The root of the complete binary tree is at 1. Each node has a level. The solution identifies tours by the smallest level node on them. For example 9->4->2->5->10->21 is identified by 2, and it's added to the solution, when going through node 2. The "highest" node, thus the smallest level one will be a node from the path of v, 1 (endpoints included), and because it's a complete binary tree, this path has at most log(N) nodes.
Well, the solution of the B problem makes me feel kinda stupid. Well, thanks for the editorial anyway!
Could you please prove both "obvious" parts of div2B? Why there is no sulution when parity is different and why all the cells exist if we set first (n — 1) * (m — 1) as we wish? There may be problems with the one which is in right-bottom corner.
I don't understand solution for 894B at all. I've read editorial many times, I've read comments. The explanation doesn't make sense to me at all.
First, it's absolutely not obvious to me why parity of n and m should be the same if k = -1. Why it couldn't be some combination of 1s and -1s when the number of -1s in each row and column is odd?
Second, I absolutely don't understand why any random rectangle of size (n — 1), (m — 1) can be extended to proper n, m rectangle. In particular, what if parity of -1s in added row and column is different. I don't see why it shouldn't happen.
P.S. With such cryptic explanation it could be the same not having editorial at all. If amount of effort to understand solution from reading others submissions is the same as amount of effort to read editorial, then we don't need editorial.
Observe that the product of all the numbers in the rectangle is equal to both the product of all the columns as well as the product of all the rows. This means that
You can use this to prove why the special case mentioned above does not work, while all other cases do.
Thanks, now I understand why answer is
0whenk == -1 && n % 2 != m % 2.But it's still not clear to me why if you are extending some randomly generated rectangle (marked as
x), it could not be the case when parity of-1sin new extended row and new extended column is different, say something like this:So as I understand by extending row or column, you are forced to put certain digit. So in case when parity of
-1sin added column or row is different then no matter what you put inyyou can't make them both equal correct parity.By a similar argument, the product of the incomplete last row (excluding the final element) must be equal to the product of the incomplete last column. This is not the case in your example.
I know it must be equal but since we have randomly generated square (let's assume we denote these numbers as letters a..i):
a b c
d e f
g h i
Then to extend this square, we are forced to put certain number 1 or -1 so that for example, a * b * c * x == k.
Obviously, for a any given a, b, c there is only one choice of x to make a * b * c * x == k.
Now, it's not clear to me that in a new extended square:
a b c x
d e f y
g h i z
f g h r
There would be x * y * z * r != f * g * h * r in case parity of -1s in x, y, z, r and f, g, h, r is different.
When we put x, y, z and f, g, h in one forced choice to satisfy existing numbers (for example: a * b * c * x == k). There is no guarantee that this case wouldn't happen.
Fix the upper 3-by-3 matrix. Then
This implies that
because when we substitute with the above two expressions, we cancel out all the variables of the upper 3-by-3 matrix and end up with
which is true. Now we can just select the value of
which works.
Big thanks Benq!!!
To me it was a very big surprise that, you can swap from:
a * b * c * x = k
to:
a * b * c * k = x
(in case when a, b, c, x, k are numbers either -1 or 1)
In my head, I couldn't do that swap since I operated them as general integers instead of doing special case when only integers 1 and -1.
I know I'm late but thanks for this, this is amazing.
In fact, I found another problem on Xor on grid which uses the same idea. I immediately got solution to that problem after I read your comment. I couldn't resist thanking.
Thanks a lot, Benq amazing explanation.
" If amount of effort to understand solution from reading others submissions is the same as amount of effort to read editorial, then we don't need editorial."
well said (y)
In problem C this test ->
31 15 25The author's solution produces ->
51 1 15 1 25so if these numbers are valid how come
gcd(15, 25) == 5isn't in thegcd set {1, 15, 25}?UPD : I'm sorry I think I misunderstood the problem, I was thinking the input set was the gcd(a[i], a[j]) for every pair in the sequence! this variation (present in the contest is a bit easier!)
can someone help me find a solution to this variation I thought the problem was? NOIRP
5 is the number of solution
For problem B:
It’s obvious that we could get an unique answer right.
But could anyone help me to understand the unique answer is always a valid answer.
For example I put 1 in all (n-1,m-1)entries and I got a valid answer,now I change some entries from 1 to -1 ,here why can we guarantee that we could get a valid answer rather than a conflict answer
Let's assume our k=1 and look at a particular row. If the product of the first m-1 elements in this row is equal to 1 we set the mth element to 1 and the row is valid since the product of the m elements remains 1. If the product the first m-1 elements i equal to -1 we set the mth element to -1 and the row becomes valid since the product of the m elements becomes 1. We can repeat the process for all the rows and columns to make them valid. The same approach works if k=-1, although we have to handle the edge cases where m is odd and n is even and n is odd and m is even.
I’am sorry but it seems that you didn’t solve my confusion
You just say
repeat the process for all rows and columns to make them valid.Here I understand right,but why can you guarantee we can put the (n,m) entry to satisfy both n-row and m-column after doing the above steps,could you please prove it,thx:)That's a good point I didn't consider that. Thinking about it for a bit I came up with the following argument.
Let's consider the case k=1 and two cases. First case we have an even number of -1s in the sub-matrix A[1...n-1][1...m-1]. With our construction each row product is 1 so the total product of the of the sub-matrix A[1...n-1][1...m] is 1. This means the column A[1...n-1][m] must also have an even number of -1s, since if it had an odd number of -1s the total product of the sub-matrix A[1...n-1][1...m] would be -1. With a similar argument we can show we will also have an even number -1s in the row A[n][1...m-1]. This means in this case we can set A[n][m] to 1 and the product of the n-row and m-column will be 1.
For the case where there are an odd number of -1s in the submatrix and k=1 the argument is similar but now A[1...n-1][m] and A[n][1...m-1] will have an odd number of 1s and we set A[n][m]=-1.
The same argument should work if k=-1 assuming there are valid solutions.
Excellent!
Now you have solved my confusion!
The case for k=-1 could be a little different though.
Thx:)
For Problem B:
I have read and understood the editorials and I am trying to implement the solution but am getting the wrong answer, can someone assist me. Here is my logic:
Is there something wrong with this logic? edge cases? I have been trying for a few hours now and I can't figure out whats wrong.
Your logic is correct, but you have to take modulo by 10^9 + 7.
Why was the constraints for problem C this low? if it was for the checker it can be implemented in O(nlog(n)). You can use the implementation for problem 475D - CGCDSSQ.
The checker should be easy and readable so we reduced the constraints from 1e5 to 1000. And reducing it to 1000 will make some contestants come up with some other constructive ways to solve the problem. It's very ok for a Div.2 C.
Auto comment: topic has been updated by whfym (previous revision, new revision, compare).
In problem B what is parity ? and what is the proof behind the solution in editorial ?
For B, how can this code not be TLE? 32471265. Owner does fast exponentiation (binpow) on this way, to compute x^k :
If k is even, then binpow(x, k) = binpow(x, k/2) * binpow(x, k/2);
This way, the binpow function will be called k times (and not log(k)). As k can be large, it should TLE. On my computer it is veryy long. Why not on codeforces?? Is there an option i didn't know?
I think it's because the compiler optimization sees that it's the same call and same result and must do some kind of auto-memoization. When I add a global counter variable and increment it each time we call the function, it takes ages, but it works instantly without this counter variable.
piece of shit
So in 894C, it's valid to have a number in S which is not gcd of any sub array?
For example, with this sample test:
4
2 4 6 12
The output (from the above tutorial) will be:
2 2 4 2 6 2 12
From the above result, 2 will be gcd of all sub-arrays, and 4, 6, 12 are not gcd of any sub-array.
Sorry got it, I thought i must be different than j.
May I ask for a more specific tutorial on question B? Too many "obvious" in the tutorial provided and I cannot get the point.
We can only use 1 and -1 because otherwise the product won't be 1 or -1.
First for the invalid case, it's because product of all row == product of all column == product of entire rectangle. So you can't have k = -1 with odd row and even column (and vice versa) because row product == 1 and column product == -1 which is different.
Now for the valid case, let's say we want to fill n*m rectangle. The formula given in editorial pow(2, [(n - 1) * (m - 1)]) can be rephrased as: The value of the last row and the last column is predetermined by the first (n-1) row and (m-1) column. Also, the formula implies that any arbitrary filling of the first (n-1) row and (m-1) column is always valid; We can always correct any wrong product with the last row and last column.
To see why any arbitrary filling is correct, consider the following 4x4 rectangle (it can easily be generalized to any other size), and k == 1. Suppose we have randomly filled 3x3 with 1 and -1:
xxxa
xxxb
xxxc
def?
Where x is the random filled value. a-f and ? is the value we will insert to correct the product of the 3x3 rectangle.
First, notice that the value a-f is already predetermined. For example, if the product of the first row (without "a") is -1, then "a" must be -1 because k == 1. "a" == 1 otherwise. The same goes for bcdef.
Now the part that may get confusing is, how do we fill the "?". If the sign of a*b*c != d*e*f, then obviously the rectangle is invalid. For example a*b*c = -1, and d*e*f = 1. Then we cannot correct both product with a single "?". Fortunately, we can prove that it is impossible for (a*b*c) to be different from (d*e*f).
Consider the 3x3 rectangle. Observe that a == product of first row, b == product of second row and c == product of third row. This means that a*b*c == product of all row(3*3) == product of 3*3 rectangle.
Similar thing with d,e,f. d == product of first column, e == product of second column, and f == product of third column. This means that d*e*f == product of all column(3*3) == product of 3*3 rectangle.
But since a*b*c == d*e*f == product of 3*3 rectangle, they must have the same sign, so the value of "?" is also predetermined!
You can use very similar logic to prove things for k = -1. Sorry if the proof is not mathematical enough, but I hope it's clear.
*Just noticed there are many users already explaining B above. If you have trouble understanding mine, you can try the others
Yes I completely understand now, thanks you. Actually I could understand the idea here but just could not find the proof. The critical fact here is abc = cdf, and it is the key to prove that for any filling of the (n-1)*(m-1) matrix, we can always generate one and only one matrix of size n*m.
Thank you for writing good editorial for this problem!
To me it was very big surprise. In fact, I suffered a lot till Benq explained it to me. I don't think I would find this observation even after a week of thinking because I would overlook this.
Since numbers are only 1 and -1 we can change the following equation:
x1 * x2 * x3 * a == k
To:
x1 * x2 * x3 * k == a
I checked this observation on concrete numbers in all cases, it works:
k == -1, odd number of -1s in x1, x2, x3:
1 -1 1 1 = -1, after swapping a and k equality still holds 1 -1 1 -1 = 1.
For all others cases it's the same.
I have to remember this nice property!
Thanks, glad I could be of help.
Very nice analogy!
A doubt in b's tutorial,providing random values from the set {-1,1} for n-1 rows and m-1 columns,we would have definite values for nth row and mth column entries.Now for a[n][m](value at index n,m)what if we need to have contrary values?
You'll have contrary values on a[n][m] only if k=-1 and n%2 != m%2 (try on a simple example to see why), That's why in this case, answer is 0. In all other cases, the value on a[n][m] will be uniquely defined.
Why always in queue?
As regards D. It can be solved in O((n+m)logn). You don't have to do any sort — all the arrays are sorted, so you just merge them in linear time. Also you do not need any binary search — for each sorted query just progress the pointer in sorted distances array until distance is too big for that query.
Wow!
Yes,it can be solved in O((n+m)logn),thanks a lot for pointing it out!
I also did not manage to edit my post yesterday (cf was quite slow) but memory is linear O(n+m) — you just compute the size of the subtree and fill that space with sorted distances. As regards queries, you remove them from children, merge them in ascending order and assign to parent. There is no need to duplicate or to keep old values in children.
Can someone please help me find the bug in this:
http://codeforces.com/contest/894/submission/32906228
its code for problem E. I did: 1) SCC 2) DAG construction 3) DP
IN problem C If Input 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Participant's output 10 15 14 13 12 11 10 9 8 7 6 Jury's answer 29 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 1 10 1 11 1 12 1 13 1 14 1 15 Checker comment wrong answer Integer 2 appears in the set, but not produced by the sequence.
I am not able to find why It is giving wrong answer gcd(14,12) = 2 then why it is saying that we can't produce 2 by sequence. Can anyone help me??
Your output sequence can't produce 2. 10 15 14 13 12 11 10 9 8 7 6 You can't find a range of number which GCD = 2 in your sequence. Please read the statement carefully :)
In Problem C, My Solution: http://codeforces.com/contest/894/submission/33303911
My Solutions is printing every element Twice because GCD(9,9) = 9.
I am not able to find why It is giving the wrong answer on test 15.
Please read the statement carefully.
And this input may help you:
3
2 12 18
Your output: 2 2 12 12 18 18
GCD(12,18)=6
However 6 is not in the set.