Converting 2D Dominance Relation to a DAG

#	User	Rating
1	ecnerwala	3649
2	Benq	3581
3	orzdevinwang	3570
4	Geothermal	3569
4	cnnfls_csy	3569
6	tourist	3565
7	maroonrk	3531
8	Radewoosh	3521
9	Um_nik	3482
10	jiangly	3468

#	User	Contrib.
1	maomao90	174
2	awoo	164
3	adamant	161
4	TheScrasse	159
5	nor	158
6	maroonrk	156
7	-is-this-fft-	151
8	SecondThread	147
9	orz	146
10	pajenegod	145

Hi all,

Consider n lattice points in a 2D grid {(x₁, y₁)....(x_n, y_n)}. A point (x₁, y₁) is said to dominate another point (x₂, y₂) if and only if x₁ > x₂ and y₁ > y₂. Obviously this dominance relation defines a DAG: G has an edge 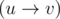$\text{[math]}$ if point u dominates point v. Let us call this the dominance graph.

My question is this, is it possible to efficiently (say in time O(nlog(n))) compute the dominance graph?

Obviously, the dominance graph could have O(n²) edges. For example, if every point lies on the x = y line, then each point would dominate all points below it, giving us ⁿC₂ edges. But I would be happy with a graph that would INDUCE the dominator graph by transitivity.

So, in the example above, instead of ⁿC₂ edges, it is sufficient to keep n - 1 edges.

This is not from any contest. It's just something that I'm curious about and haven't been able to make progress on. I don't even know if this graph is going to be sparse enough to be explicitly computed.

Comments (13)

Write comment?

amnesiac_dusk

5 years ago, # |

+21

The dominance graph can have O(n^2) edges. For example- in this case-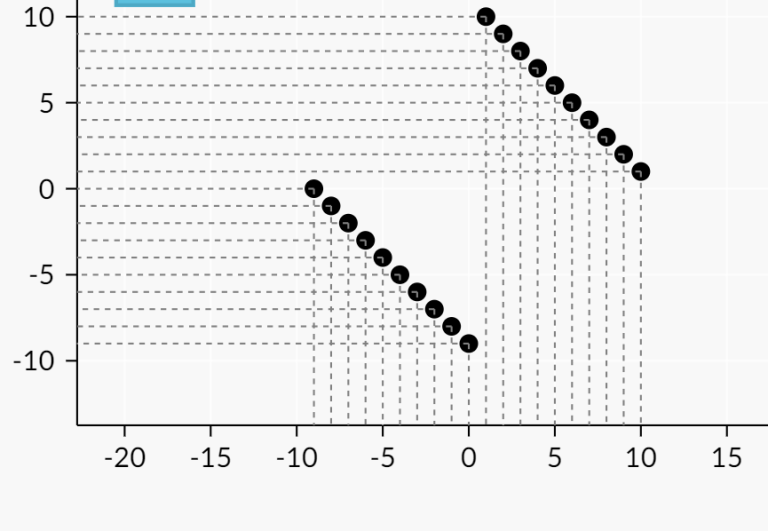

→ Reply

proofbycontradiction

5 years ago, # ^ |

Wow. That absolutely settles it.

How about this follow-up question: If we decided to clump the nodes that have the same ancestors and the same descendants, then would the graph be smaller than O(n^{2})?

Because we have derived this graph from such a compact representation, I want to see if the graph has some interesting properties.

← Rev. 4 →

Edit: Its possible with some additional nodes. See radoslav11's comment below.

I don't think there will be less than O(n^2) edges. Just move any of these lines parallely towards the other and we will have different nodes having different set of ancestors. While all over it will still be O(n^2).

Also, how did you generate this graph?

I used csacademy geometry tool.

radoslav11

+16

You can actually create a dominance graph with some additional nodes that will have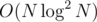 $\text{[math]}$ edges.

The overall idea is to imagine you have a 2D segment tree and for each node in it create an additional vertex that has directed edges to its children nodes. We will also add edges from the leaf nodes of the tree to the corresponding vertices at that coordinate. Then if we want to add an edge from a vertex to all other vertices that are dominated by it, we do 2D query for the interval [(x_i + 1, y_i + 1), (∞, ∞)] and add directed edges from the current node to the corresponding nodes. This way if we use dynamic segment tree we will have only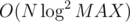 $\text{[math]}$ edges and the amount of vertices will be $\text{[math]}$ .

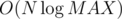By compressing the coordinates we can easily achieve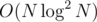 $\text{[math]}$ edges and $\text{[math]}$ memory.

The same thing can be done with Quad-tree and in practice it should perform better.

← Rev. 2 →

+10

Your construction is quite ingenious.

So, if I understand your idea correctly, the length of the maximum antichain doesn't change in your new construction. Could you confirm that?

If you don't include the additional nodes in the antichain — yes, because you can think of the additional nodes as blocks of compressed edges.

If you do include them, I again think the size of the antichain will stay the same. But I unfortunately don't have a nice proof for that.

On a side note, I also found an easier and better way to compress the dominance graph. It works in $\text{[math]}$ and the memory is also $\text{[math]}$ . If anyone is interested I can explain the idea. In short it's based on persistent trees and going through the points from right to left, based on their X.

I am VERY interested.

For convenience, imagine that all X are different. Also we will compress the coordinates.

Now sort the points in decreasing order of their X and go through them one by one. If the current point has coordinates (x_i, y_i), we need to add edges from it to all points that we have already passed with a larger y.

Let's maintain a 1D persistent segment tree. Initially build it like normally creating O(n) new vertices and linking them to their children. You can think about it as a vertical line, where each leaf is linked to the points with the corresponding Y that we have already passed.

So back to looking at a point (x_i, y_i). We basically want to add edges from it to the part of the "line"/persistent tree that is the interval [y_i + 1;n]. Well we will make a query on the tree and add $\text{[math]}$ edges to the needed nodes. With this we have finished adding the edges from point i.

Now the last part is to add the point to our "line". We create $\text{[math]}$ new vertices for the path from the root of the persistent tree to the leaf for y_i. We will also add edge from the new leaf to the vertex i. Now we add edges from this new path to its prototype and replace the old path with the new one in the "line".

This way the complexity and memory will be $\text{[math]}$ .

Oh, I understand. This construction is quite magical.

Again, just to reconfirm, in the final graph we will have ...

... all the edges of the persistent segment tree + edges from leaf to relevant nodes of the previous version of the tree.

Yep.

proofbycontradiction's blog