Cheers everyone.
Today, on June 13 at 10:00 MSK the third and final qualification round of Yandex.Algorithm 2016 tournament will take place. I am the author of all tasks in this round. I wish to thank Ivan Gassa Kazmenko, Oleg snarknews Khristenko, and espically Aleksey Chmel_Tolstiy Tolstikov and Maxim Zlobober Akhmedov for their immense contribution to problems preparation. I also thank Yandex employees who were involved in testing this round.
Best of luck!
UPD: the round is complete! Congratulations to Um_nik, who was the only one to solve all problems!
You can find the elimination standings here. Congratulations to 25 best participants!
Editorial here










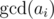 . Actually, it may be zero,
. Actually, it may be zero, 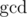 or its divisor.
or its divisor.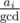 beads of
beads of 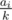 beads of color
beads of color 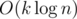 time, for a total complexity of
time, for a total complexity of  .
.
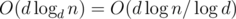 where
where  time? Maybe even faster?
time? Maybe even faster? time.
time.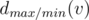 for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain
for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain 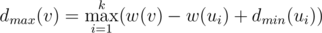 . Thus, if we know
. Thus, if we know 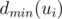 for all children, the value of
for all children, the value of 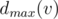 can be determined.
can be determined.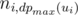 is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most
is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most 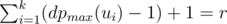 . Indeed, if all the numbers
. Indeed, if all the numbers 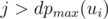 should also be greater than
should also be greater than 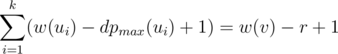 numbers
numbers 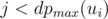 , and
, and 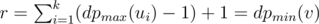 .
.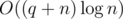 solution. Estimate
solution. Estimate 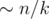 non-leaf vertices, thus the total number of queries will be
non-leaf vertices, thus the total number of queries will be 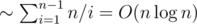 (harmonic sum estimation). To sum up, this solution works in
(harmonic sum estimation). To sum up, this solution works in 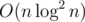 time.
time.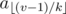 . One can show that there are only
. One can show that there are only 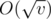 different elements that can be the parent of
different elements that can be the parent of 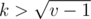 , the index of the parent is less that
, the index of the parent is less that 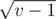 , and all
, and all 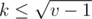 produce no more than
produce no more than 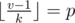 for
for 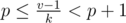 ,
, 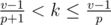 ,
, 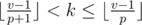 . For every
. For every 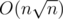 queries to the delta array (as this is the number of different child-parent pairs for all
queries to the delta array (as this is the number of different child-parent pairs for all  ? In
? In 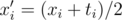 . If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because
. If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because 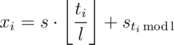 holds, because the full cycle is executed
holds, because the full cycle is executed 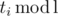 more first commands. From this, we deduce
more first commands. From this, we deduce 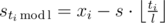 .
.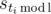 ; they are fixed from now on. One more important fixed value is
; they are fixed from now on. One more important fixed value is 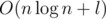 , or even in
, or even in 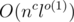 , for example?)
, for example?)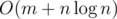 using an efficient data structure like
using an efficient data structure like 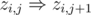 . As
. As 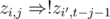 (here
(here 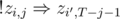 for a similar reason. In this,
for a similar reason. In this, 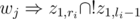 and
and 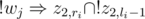 are pretty much self-explanating. A conflicting pair of teachers
are pretty much self-explanating. A conflicting pair of teachers 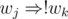 ,
, 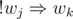 .
. .
.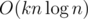 solution? An
solution? An 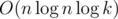 solution? Maybe even better? (Hint: the modulo should be an appropriately chosen prime number for a fast solution =)).
solution? Maybe even better? (Hint: the modulo should be an appropriately chosen prime number for a fast solution =)).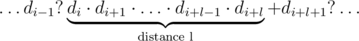
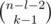 . A similar reasoning implies that if the digit
. A similar reasoning implies that if the digit 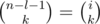 .
.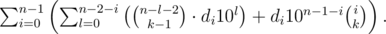
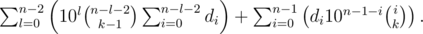
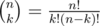 , so it is enough to know all the numbers
, so it is enough to know all the numbers 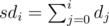 . The rest is simple evaluation of the above sums.
. The rest is simple evaluation of the above sums.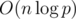 , because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of
, because the common algorithms for modular inverses (that is, Ferma's little theorem exponentiation or solving a diophantine equation using the Euclid's algorithm) have theoritcal worst-case complexity of 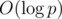 . However, one can utilize a neat trick for finding modular inverses for first
. However, one can utilize a neat trick for finding modular inverses for first 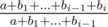 . Now, with that ratio determined unambigiously for each addition upgrade, every addition has actually become a multiplication. =) So we have to compute the ratios for all additions (that is, we sort
. Now, with that ratio determined unambigiously for each addition upgrade, every addition has actually become a multiplication. =) So we have to compute the ratios for all additions (that is, we sort 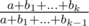 . As
. As  and
and  we should compare the products
we should compare the products 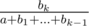 . Now, the numerator is up to
. Now, the numerator is up to 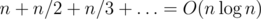 (which is the famous harmonic sum). Using one of the approaches discussed above, one obtains a solution with complexity of
(which is the famous harmonic sum). Using one of the approaches discussed above, one obtains a solution with complexity of 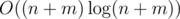 .
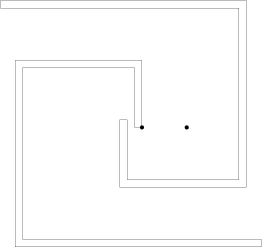
.
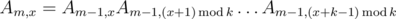 . This formula allows us to count
. This formula allows us to count 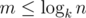 and all
and all 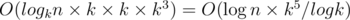 time. Now, upon having all
time. Now, upon having all 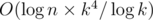 time, which fits the limits by a margin.
time, which fits the limits by a margin.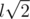 ,
, 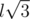 . A cube must contain exactly
. A cube must contain exactly 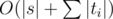 . The code for this problem pretty much consists of the above formula, so implementation is as easy as it gets once you grasp the idea. =)
. The code for this problem pretty much consists of the above formula, so implementation is as easy as it gets once you grasp the idea. =) we get nothing, and with probability
we get nothing, and with probability 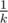 we get out item with level distributed as usual. Denote
we get out item with level distributed as usual. Denote 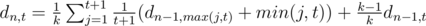 , which is equal to
, which is equal to 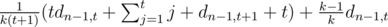 =
=  . To get the answer note that
. To get the answer note that 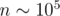 .
.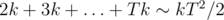 . So, in common case our level can get up to about
. So, in common case our level can get up to about 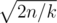 , which does not exceed
, which does not exceed 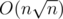 complexity is obtained (here we assert that
complexity is obtained (here we assert that 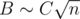 , and constant
, and constant 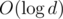 , so our solution has
, so our solution has 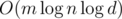 complexity. However, great caution is needed to achieve a practical solution.
complexity. However, great caution is needed to achieve a practical solution. new nodes are created on every query (which is impossible to achieve with any kind of propagation which would require at least
new nodes are created on every query (which is impossible to achieve with any kind of propagation which would require at least 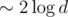 ), and also nodes need to store less information and become lighter this way. Also, no "push" procedure is required now.
), and also nodes need to store less information and become lighter this way. Also, no "push" procedure is required now.
