Всем привет.
Сегодня, 13 июня в 10:00 MSK состоится третий и последний отборочный раунд Яндекс.Алгоритма 2016. Я являюсь автором всех задач этого раунда. Благодарю за помощь Ивана Gassa Казменко, Олега snarknews Христенко, и особенно Алексея Chmel_Tolstiy Толстикова и Максима Zlobober Ахмедова, которые внесли большой вклад в подготовку задач. Также благодарю сотрудников Яндекса, которые прорешивали раунд.
Желаю удачи!
UPD: раунд завершен! Поздравляем Um_nik, единственного, решившего все задачи!
Общую таблицу результатов отборочного этапа можно найти здесь. Поздравляем 25 лучших участников, прошедших в финал!
Разбор (пока что только на английском) можно найти тут











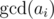 . Actually, it may be zero,
. Actually, it may be zero, 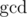 or its divisor.
or its divisor.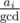 beads of
beads of 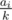 beads of color
beads of color 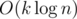 time, for a total complexity of
time, for a total complexity of  .
.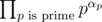 , where
, where 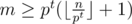 ; there is a case when the new number divides some greater power of
; there is a case when the new number divides some greater power of 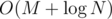 solution is possible.
solution is possible.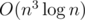 solution, also probably a highly optimized
solution, also probably a highly optimized 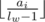 (be careful not to divide by zero of
(be careful not to divide by zero of  solution. I tried to make sure no
solution. I tried to make sure no 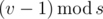 . We have reduced the problem to the similar one concerning the subtree; treat it recursively. The sequence of sizes provides all the necessary information; thus, the depth can be found in
. We have reduced the problem to the similar one concerning the subtree; treat it recursively. The sequence of sizes provides all the necessary information; thus, the depth can be found in 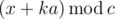 , which is the same set of ends as the periodical sequence with diffence
, which is the same set of ends as the periodical sequence with diffence 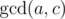 ; thus the
; thus the 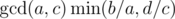 . Do not forget to use 64-bit integers for multiplication.
. Do not forget to use 64-bit integers for multiplication.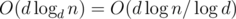 where
where  time? Maybe even faster?
time? Maybe even faster?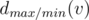 for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain
for the maximal possible result if the maximizing/minimizing (depending on the lower index) player starts. From the previous discussion we obtain 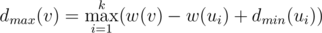 . Thus, if we know
. Thus, if we know 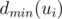 for all children, the value of
for all children, the value of 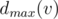 can be determined.
can be determined.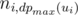 is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most
is minimal. For every arrangement, the minimizing player can guarantee himself the result of at most 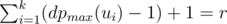 . Indeed, if all the numbers
. Indeed, if all the numbers 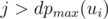 should also be greater than
should also be greater than 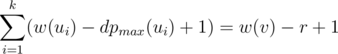 numbers
numbers 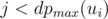 , and
, and 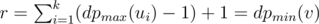 .
.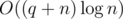 solution. Estimate
solution. Estimate 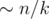 non-leaf vertices, thus the total number of queries will be
non-leaf vertices, thus the total number of queries will be 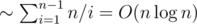 (harmonic sum estimation). To sum up, this solution works in
(harmonic sum estimation). To sum up, this solution works in 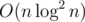 time.
time.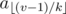 . One can show that there are only
. One can show that there are only 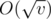 different elements that can be the parent of
different elements that can be the parent of 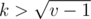 , the index of the parent is less that
, the index of the parent is less that 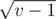 , and all
, and all 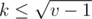 produce no more than
produce no more than 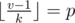 for
for 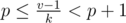 ,
, 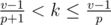 ,
, 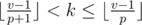 . For every
. For every 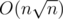 queries to the delta array (as this is the number of different child-parent pairs for all
queries to the delta array (as this is the number of different child-parent pairs for all 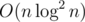 ? In
? In 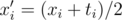 . If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because
. If the division fails to produce an integer for some entry, we must conclude that the data is inconsistent (because 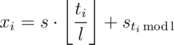 holds, because the full cycle is executed
holds, because the full cycle is executed 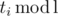 more first commands. From this, we deduce
more first commands. From this, we deduce 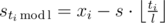 .
.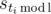 ; they are fixed from now on. One more important fixed value is
; they are fixed from now on. One more important fixed value is 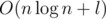 , or even in
, or even in 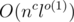 , for example?)
, for example?)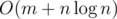 using an efficient data structure like
using an efficient data structure like 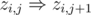 . As
. As 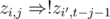 (here
(here 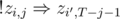 for a similar reason. In this,
for a similar reason. In this, 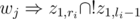 and
and 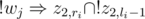 are pretty much self-explanating. A conflicting pair of teachers
are pretty much self-explanating. A conflicting pair of teachers 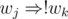 ,
, 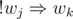 .
.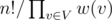 , where
, where 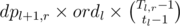 , where
, where  .
.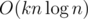 ? За время
? За время 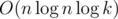 ? Может быть, еще быстрее? (Подсказка: для быстрого решения необходим удачно подобранный простой модуль. =))
? Может быть, еще быстрее? (Подсказка: для быстрого решения необходим удачно подобранный простой модуль. =))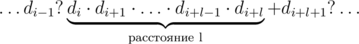
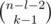 . Рассуждая схожим образом, получим, что если цифра
. Рассуждая схожим образом, получим, что если цифра 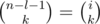 .
.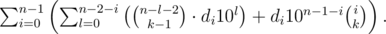
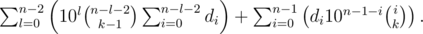
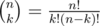 , поэтому достаточно вычислить все
, поэтому достаточно вычислить все 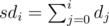 . Осталось просто просуммировать произведения этих величин.
. Осталось просто просуммировать произведения этих величин.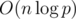 , поскольку стандартные алгоритмы для поиска обратных по модулю (а именно, малая теорема Ферма с бинарным возведением в степень и решение диофантова уравнения при помощи обобщенного алгоритма Евклида) имеют верхнюю оценку сложности
, поскольку стандартные алгоритмы для поиска обратных по модулю (а именно, малая теорема Ферма с бинарным возведением в степень и решение диофантова уравнения при помощи обобщенного алгоритма Евклида) имеют верхнюю оценку сложности 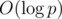 . Однако, можно воспользоваться интересным трюком и вычислить все обратные элементы для первых
. Однако, можно воспользоваться интересным трюком и вычислить все обратные элементы для первых 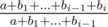 . Теперь, когда это отношение однозначно определилось для каждого прибавления, мы можем считать любое прибавление умножением. =) Теперь посчитаем такие отношения для всех прибавлений (т.е., отсортируем
. Теперь, когда это отношение однозначно определилось для каждого прибавления, мы можем считать любое прибавление умножением. =) Теперь посчитаем такие отношения для всех прибавлений (т.е., отсортируем 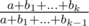 . Поскольку
. Поскольку  и
и  , мы сравниваем произведения
, мы сравниваем произведения 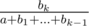 . Теперь, числитель стал всего лишь порядка
. Теперь, числитель стал всего лишь порядка 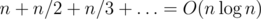 (известная сумма гармонического ряда). В зависимости от способа обработки одного сета итоговая сложность составляет
(известная сумма гармонического ряда). В зависимости от способа обработки одного сета итоговая сложность составляет 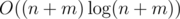 .
.
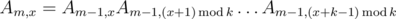 . Эта формула позволяет нам вычислить
. Эта формула позволяет нам вычислить 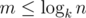 и
и 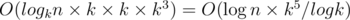 . Теперь, имея все
. Теперь, имея все 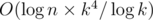 , что укладывается в ограничения с запасом.
, что укладывается в ограничения с запасом.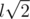 ,
, 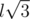 . Куб должен содержать ровно 12 пар первого типа, 12 пар второго типа и 4 пары третьего типа. Можете ли вы доказать, что это необходимое условие является достаточным для того, что конфигурация является кубом? Верно ли это, если координаты могут быть нецелыми? Можете ли вы придумать еще более простой способ проверки на куб?
. Куб должен содержать ровно 12 пар первого типа, 12 пар второго типа и 4 пары третьего типа. Можете ли вы доказать, что это необходимое условие является достаточным для того, что конфигурация является кубом? Верно ли это, если координаты могут быть нецелыми? Можете ли вы придумать еще более простой способ проверки на куб?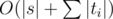 . Код по сути состоит из одной формулы, поэтому реализация получается проще некуда.
. Код по сути состоит из одной формулы, поэтому реализация получается проще некуда. нам ничего не выпадает, а с вероятностью
нам ничего не выпадает, а с вероятностью 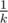 мы получаем предмет, уровень которого распределен как обычно. Обозначим за
мы получаем предмет, уровень которого распределен как обычно. Обозначим за 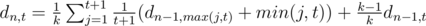 , что то же самое, что и
, что то же самое, что и 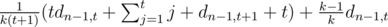 =
=  . Ответ находится как
. Ответ находится как 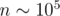 .
.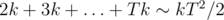 . Поэтому в общем случае уровень нашего предмета будет равен примерно
. Поэтому в общем случае уровень нашего предмета будет равен примерно 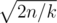 , что в наших ограничениях не превосходит
, что в наших ограничениях не превосходит 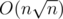 (мы опираемся на то, что
(мы опираемся на то, что 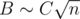 , и константа
, и константа 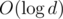 , поэтому наше решение работает за время
, поэтому наше решение работает за время 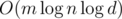 . Однако, реализовывать его надо было аккуратно.
. Однако, реализовывать его надо было аккуратно.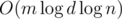 памяти, что в ML уже не влезает никак. От этого можно избавляться по-разному; например, если мы приходим в вершину, из которой надо что-то протолкнуть вниз, это значит, что весь отрезок этой вершины состоит из одинаковых чисел, поэтому ответить на запрос о сравнении можно уже сейчас.
памяти, что в ML уже не влезает никак. От этого можно избавляться по-разному; например, если мы приходим в вершину, из которой надо что-то протолкнуть вниз, это значит, что весь отрезок этой вершины состоит из одинаковых чисел, поэтому ответить на запрос о сравнении можно уже сейчас. новых вершин (с ленивым проталкиванием такого достичь не удастся, придется создавать минимум
новых вершин (с ленивым проталкиванием такого достичь не удастся, придется создавать минимум 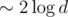 ), кроме того, вершины хранят в себе меньше информации и занимают меньше памяти. И про проталкивание чего бы то ни было думать не надо. Красота.
), кроме того, вершины хранят в себе меньше информации и занимают меньше памяти. И про проталкивание чего бы то ни было думать не надо. Красота.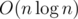 (или
(или 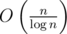 .
.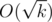 перебрать все делители
перебрать все делители 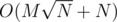 . Можно решать и быстрее, если для каждого числа сохранить список его простых делителей и поддерживать описанный выше массив только для простых чисел. Суммарный размер списков для чисел от
. Можно решать и быстрее, если для каждого числа сохранить список его простых делителей и поддерживать описанный выше массив только для простых чисел. Суммарный размер списков для чисел от 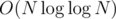 (это следует из оценки на сумму ряда
(это следует из оценки на сумму ряда 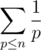 по всем простым, не большим
по всем простым, не большим 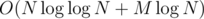 , т.к. количество простых делителей
, т.к. количество простых делителей 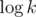 (точная верхняя оценка —
(точная верхняя оценка — 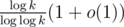 ).
).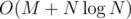 .
.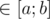 , выигрывает первый игрок, т.к. он может свести игру к предыдущему случаю, предоставив второму игроку ход в проигрышной для него ситуации.
, выигрывает первый игрок, т.к. он может свести игру к предыдущему случаю, предоставив второму игроку ход в проигрышной для него ситуации.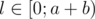 . Ситуация
. Ситуация 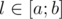 — выигрышные. Если
— выигрышные. Если 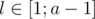 , мы не можем сходить в проигрышную ситуацию (пользуемся предположением индукции для меньших
, мы не можем сходить в проигрышную ситуацию (пользуемся предположением индукции для меньших 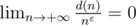 , где
, где 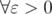
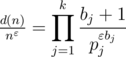
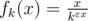 , где
, где 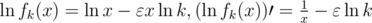
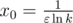 — глобальный максимум (т.к. других нулей у производной нет).
— глобальный максимум (т.к. других нулей у производной нет).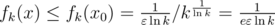
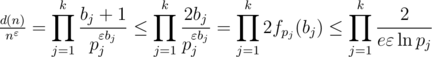
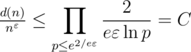
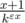 . Тогда при применении того же метода построения верхней оценки получится, что
. Тогда при применении того же метода построения верхней оценки получится, что 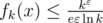 , что стремится к бесконечности с ростом
, что стремится к бесконечности с ростом 
