Hey Codeforces,
I made a post on AoPS that I thought you guys might find interesting. The original context was math contests in the US, but I think much of it applies to CS (and more generally) too.
Hey AoPS, it’s good to be back. I’m feeling a little sentimental right now, but I guess that’s alright—it’s been six years since I first found you, and it’s been a long journey since. I was a sixth grader then, just starting Mathcounts, unsure if I’d even make the school team. I fell in love with For The Win! (Alpha) and played it during lunch break, after school, even the morning before Mathcounts Nats. In ninth and tenth grade, I scoured the Olympiad fora, wondering if there existed some magic advice that could propel me all the way to MOP. I was chasing after the mathematical footsteps of my Exeter friends then, always feeling a few steps behind. And now I’ve graduated high school. Contests are over for me. It’s pencils down.
Thank you, AoPS, for the community that has made me fall in love with math, that let me hear about this school called Phillips Exeter Academy, that let me know how big I could dream. Thank you for playing Mafia and Beat the Mod with me, for showing me all the beautiful combinatorics, algebra, and number theory, for trolling with me on FTW, Fun Factory, and MathIM.¹ Over the years that I’ve known you, AoPS, I’ve done some things right and some things wrong. And I’ve learned a lot along the way. I’m here because I feel an urge to give a few tidbits back, to share some restless thoughts—thoughts I wish I’d known earlier and still don’t hear too often. These reflections are for myself as much as they are for you.
I’ll start with contests. Don’t train for them. Study math, computer science, physics, or whatever because you enjoy studying the subject, not for the sake of ego or competition. I wasn’t always great about this. In tenth grade, before my last shot at JMO, I constantly compared myself to my friends in Math Club. The olympiad loomed over me as I struggled through practice tests and problem sets. I felt dumb, inadequate, a failure each time I couldn’t solve a problem. I learned facts about symmedians and Miquel points without appreciating their greater geometric context. Not only did I enjoy math less, I also did bad math. You should rarely feel as if you’re training for a particular competition. Do math for the sake of math, please. And if you find yourself feeling pressure from a contest, try not to forget why you chose to pursue math in the first place.²
In the end, contest results don’t define you. In eleventh grade, I soared higher than thought I could in the contest world—I made USAPhO and USNCO, a combinatorics-heavy USAMO placed me into Blue MOP, and I won gold at the IOI in Kazakhstan. I felt weightless, giddy, as if I were plunging downwards on a rollercoaster ride. But the ride only lasts for a moment, and the amusement park closes soon. As senior year neared, I wasn’t sure what to expect beyond the drudgery of college apps. It felt like game over because I’d already beaten the boss. And what remained was a void that I couldn’t quite fill because I had such little anchoring outside of the contest world. Contests are fun, but outside of the amusement park, life moves on.
I received a piece of advice when I was younger (that I still hear passed around): “Don’t learn higher math in high school—you’ll have all of college to do that.” I followed this advice faithfully, but looking back, it feels so wrong. Why limit yourself to solving elementary problems when there’s so much more? Contests provide such a narrow scope and arbitrary lines—problems that fit neatly into one of four subjects, solvable within 4.5 hours. Go read a textbook on algebra or analysis instead. Take a break from USACO training. You could learn to spin up a web app or take a MOOC on machine learning. Personally, contest problems now feel like a comfort food, something to be weaned off of.
Stepping further out, there’s more to life than just math, computer science, or other technical pursuits. That’s obvious, but there is a subtler point that took me a while to appreciate. One afternoon, while taking a break from Club Running, my jogging group skipped stones into the Exeter River. A friend asked me then: “Alex, why do you troll so much?” I flicked my pebble in and watched it skip thrice. Breaking the crisp silence after the pebble’s last plop, I said on an impulse: “To hide myself.” It was September my eleventh grade year when I made that confession, to them and to myself. Like all of my Mathcounts friends, I trolled, told people my name was Charlie and that I came from Mexico. While I maintained my outlandish facade, no one could judge the real me.
It’s meaningful, it really is, to let yourself feel vulnerable. One late night at SPARC, about a month before I skipped stones that day, was the first time I let anyone know that I hadn’t been having a great time at Exeter. There’s the fake smile that came whenever someone asked about Exeter, followed by “It’s awesome!” before I’d wax on about the people, the academics, the resources, or something.³ There was also the burnout, the frustration, and the loneliness that more defined my Exeter experience then. Letting some SPARClers understand this little piece of me—that felt awesome. Although I won’t forget those tense moments between the rustling of test booklets and “Pencils down!”, it is memories like these that I hold to and cherish.
Thank you, AoPS, for leading me down this path, to all these memories. Thank you for taking the time to read this. I hope you’ll remember something and carry it with you. Feel free to comment; ask me anything you want. I hope you’ll learn something about yourself from doing math, competing in contests, and interacting with the community here. You guys have taught me so much; I’ll be forever grateful. And finally, I hope you enjoyed understanding this little piece of me.
¹ Amusingly, one particular game was my first interaction with Codeforces users chaotic_iak, Yoshiap, ksun48, and betaveros.
² Of course, contests are wonderful in providing direction and giving a little extra push. And I notably leave out college in my list of “bad motivations,” because I do think contests help a lot with that, especially if math is your thing. However, people also get into college for research, crew, and poetry.
³ Today, I can more honestly say that Exeter is indeed amazing. :)









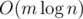 .
. 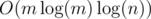 . We divide-and-conquer with respect to time by recursively solving subproblems of the form "Find all answers from time
. We divide-and-conquer with respect to time by recursively solving subproblems of the form "Find all answers from time 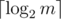 levels, edges appear a total of
levels, edges appear a total of 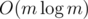 times. We process them in
times. We process them in  per edge, thus we have the desired complexity of
per edge, thus we have the desired complexity of 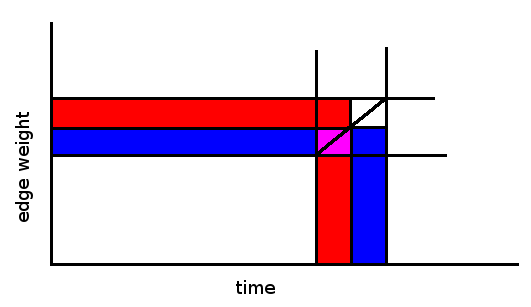
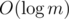 nodes covering this range. Thus we know when to add edge
nodes covering this range. Thus we know when to add edge 
