It was easy realization problem. Let's increase the variable i from 1 to n, and inside let's increase the variable j from 1 to 2·m. On every iteration we will increase the variable j on 2. If on current iteration a[i][j] = '1' or a[i][j + 1] = '1' let's increase the answer on one.
Asymptotic behavior of this solution — O(nm).
Let's calculate the answer to every block separately from each other and multiply the answer to the previous blocks to the answer for current block.
For the block with length equals to k we can calculate the answer in the following way. Let for this block the number must be divided on x and must not starts with digit y. Then the answer for this block — the number of numbers containing exactly k digits and which divisible by x, subtract the number of numbers which have the first digit equals to y and containing exactly k digits and plus the number of numbers which have the first digit equals to y - 1 (only if y > 0) and containing exactly k digits.
Asymptotic behavior of this solution — O(n / k).
Let's sort the points by increasing x coordinate and work with sorted points array next.
Let's suppose that after optimal playing points numbered l and r (l < r) are left. It's true that the first player didn't ban any of the points numbered i l < i < r, otherwise he could change his corresponding move to point l or point r (one could prove it doesn't depend on second player optimal moves) and change the optimal answer. It turns out that all the 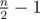 points banned by the first player have numbers outside of [l, r] segment, therefore
points banned by the first player have numbers outside of [l, r] segment, therefore 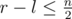 . We should notice that if the first player choosed any [l, r] for
. We should notice that if the first player choosed any [l, r] for 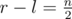 , he could always make the final points numbers located inside this segment.
, he could always make the final points numbers located inside this segment.
The second player wants to make 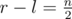 (he couldn't make less), what is equivalent if he always ban points inside final [l, r] segment (numbered l < i < r). As soon as the second player doesn't know what segment first player have chosen after every of his moves, he must detect a point which satisfies him in every first player choice. It's true number of this point is the median of set of point numbers left (the odd number) after the first player move. The number of moves of the first player left is lesser by one than moves of the second player, so the first player later could ban some points from the left and some points from the right, except three middle points. Two of it (leftmost and rightmost ones) shouldn't be banned by the second player as soon as it could increase the size of banned points from the left (or from the right), but third middle point satisfies the second player in every first player choice. This way the second player always bans the point inside final point segment.
(he couldn't make less), what is equivalent if he always ban points inside final [l, r] segment (numbered l < i < r). As soon as the second player doesn't know what segment first player have chosen after every of his moves, he must detect a point which satisfies him in every first player choice. It's true number of this point is the median of set of point numbers left (the odd number) after the first player move. The number of moves of the first player left is lesser by one than moves of the second player, so the first player later could ban some points from the left and some points from the right, except three middle points. Two of it (leftmost and rightmost ones) shouldn't be banned by the second player as soon as it could increase the size of banned points from the left (or from the right), but third middle point satisfies the second player in every first player choice. This way the second player always bans the point inside final point segment.
Thus the answer is the minimum between every of 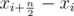 values.
values.
The main proposition to solve this problem — in the middle of every competition the sensor must be or in the top point of the wheel or in the bottom point of the wheel.
To calculate the answer we need to use binary search. If the center of the wheel moved on the distance c, then the sensor moved on the distance c + rsin(c / r), if the sensor was on the top point of the wheel in the middle, or on the distance c - rsin(c / r), if the sensor was on the bottom point of the wheel in the middle, where r — the radius of the wheel.
Asymptotic behavior of this solution —  .
.
Let's find the centers of every rectangle and multiple them of 2 (to make all coordinates integers).Then we need to by the rectangle door, which contains all dots, but the lengths of the sides of this door must be rounded up to the nearest integers.
Now, let's delete the magnets from the door one by one, gradually the door will decrease. Obviously every time optimal to delete only dots, which owned to the sides of the rectangle. Let's brute 4k ways, how we will do delete the magnets. We will do it with helps of recursion, every time we will delete point with minimum or maximum value of the coordinates. If we will store 4 arrays (or 2 deques) we can do it with asymptotic O(1). Such a solution works O(4k).
It can be easily shown that this algorithm delete always some number of the leftmost, rightmost, uppermost and lowermost points. So we can brute how k will distributed between this values and we can model the deleting with helps of 4 arrays. This solution has asymptotic behavior O(k4).
To calculate the answer on every query let's use the formula 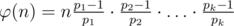 , where p1, p2, ..., pk — all prime numbers which divided n. We make all calculations by the module 109 + 7
, where p1, p2, ..., pk — all prime numbers which divided n. We make all calculations by the module 109 + 7
Let's suppose that we solving problem for fix left end l of the range. Every query now is a query on the prefix of the array. Then in formula for every prime p we need to know only about the leftmost position of it. Let's convert the query in the query of the multiple on the prefix: at first init Fenwick tree with ones, then make the multiplication in points l, l + 1, ..., n with value of the elements al, al + 1, ..., an. For every leftmost positions of prime p make in position i the multiplication in point i on the 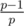 . This prepare can be done with asymptotic
. This prepare can be done with asymptotic 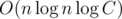 , where C — the maximum value of the element (this logarithm — the number of prime divisors of some ai).
, where C — the maximum value of the element (this logarithm — the number of prime divisors of some ai).
We interest in all leftmost ends, because of that let's know how to go from the one end to the other. Let we know all about the end l — how to update the end l + 1? Let's make the multiplication in the Fenwick tree in the point l on the value al - 1. Also we are not interesting in all prime numbers inside al, so let's make the multiplications in point l on the all values 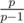 . But every of this prime numbers can have other entries which now becoming the leftmost. Add them with the multiplication which described above. With helps of sort the transition between leftmost ends can be done in
. But every of this prime numbers can have other entries which now becoming the leftmost. Add them with the multiplication which described above. With helps of sort the transition between leftmost ends can be done in 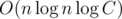 .
.
To answer to the queries we need to sort them in correct order (or add them in the dynamic array), and to the get the answer to the query we will make  iterations. So total asymptotic behavior of solution is
iterations. So total asymptotic behavior of solution is 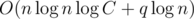 iterations and
iterations and 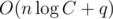 additional memory.
additional memory.
Let's describe the greedy algorithm, which allows to solve the problem for every k > 2 for every string S.
Let's think, that we always reverse some prefix of the string S (may be with length equals to one). Because we want to minimize lexicographically the string it is easy to confirm that we will reverse such a prefixes, which prefix (after reversing) is equals to the minimal lexicographically suffix of the reverse string S (let it be Sr) — this is prefix, which length equals to the length of the minimum suffix Sr (the reverse operation of the prefix S equals to change it with suffix Sr).
Let the lexicographically minimal suffix of the string Sr is s. It can be shown, that there are no 2 entries s in Sr which intersects, because of that the string s will be with period and minimal suffix will with less length. So, the string Sr looks like tpsaptp - 1sap - 1tp - 2... t1sa1, where sx means the concatenation of the string s x times, a1, a2, ..., ap — integers, and the strings t1, t2, ..., tp — some non-empty (exclude may be tp) strings, which do not contain the s inside.
If we reverse some needed prefix of the string s, we will go to the string S', and the minimal suffix s' of the reversing string S'r can't be lexicographically less than s, because of that we need to make s' equals to s. It will helps us to increase prefix which look like sb in the answer (and we will can minimize it too). it is easy to show, that maximum b, which we can get equals to a1 in case p = 1 и 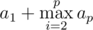 (in case if p \geq 2$). After such operations the prefix of the answer will looks like sa1saitisai - 1... sa2t2. Because t_{i} — non-empty strings we can not to increase the number of concatenations s in the prefix of the answer. The reversing of the second prefix (sai...) can be done because k > 2.
(in case if p \geq 2$). After such operations the prefix of the answer will looks like sa1saitisai - 1... sa2t2. Because t_{i} — non-empty strings we can not to increase the number of concatenations s in the prefix of the answer. The reversing of the second prefix (sai...) can be done because k > 2.
From the information described above we know that if k > 2 for lost string we need always reverse prefix, which after reversing is equals to the suffix of the string Sr which looks like sa1. To find this suffix every time, we need only once to build Lindon decomposition (with helps of Duval's algorithm) of the reverse string and carefully unite the equals strings. Only one case is lost — prefix of the lost string does not need to be reverse — we can make the concatenation of the consecutive reverse prefixes with length equals to 1.
Because for k = 1 the problem is very easy, we need to solve it for k = 2 — cut the string on the two pieces (prefix and suffix) and some way of their reverse. The case when nothing reverse is not interesting, let's look on other cases:
Prefix do not reverse. In this case always reversing suffix. Two variants of the string with reverse suffix we can compare with O(1) with helps of z-function of the string Sr#S.
Prefix reverse. To solve this case we can use approvals from the editorial of the problem F Yandex.Algorithm 2015 Round 2.2 which was written by GlebsHP and check only 2 ways of reversing prefix. We need for them to brute the reverse of suffixes.
It is only need in the end to choose from 2 cases better answer. Asymptotic behavior of the solution is O(|s|).







