(this was originally intended as a comment to another post, but it turned out very lengthy, so I separated it into its own post)
As it's often in debates, I think in this one there is too much polarization on both sides (people just attack each other), and a lot of ambiguity. I think there are some points to be made.
Premise
Let's be kind to each other. Like it or not, this is just a current trend in the history of Codeforces, and it too will pass. No need to attack anyone personally. If you want to criticize, let's provide constructive suggestions.
I've set contests before too, and I know that setting problems and coordinating is a very difficult job. It requires a lot of hard work, skill, experience, and patience. So like Anton's and other coordinators' style or not, let's not forget that they have done a lot of work, and let's thank them for that. Thank you!
It's also very mean to single out one person for the possible issue. While Anton may have a lot of impact here, there are many moving factors at play, and let's consider it as a "trend", and not particularly tie it to a single person. Let's discuss the "trend" itself and how we can possibly make thing better if needed. I also personally enjoy a lot of Anton's problems too, even though I find them maybe too much math/adhoc/etc heavy (especially when there are several in a row). But let's discuss this in depth below.
I also don't find comparison to Atcoder fully valid. If you look at ABC and ARCs, you will find plenty of algorithms, data structures, and so on. Sure, AGC may be skewed towards adhoc and math, but that's not only what Atcoder is.
Some fun observation: I find a lot of very high rated people really enjoy AGCs, and adhoc/constructive/etc problems. I personally can't really appreciate AGC beauty myself (probably because I am less skilled and don't usually get to problem C/D), and I think similar thing happens here. Very high skilled people may like adhoc/etc more for different reasons (for example, they may find a lot of DP/etc very standard. It's probably easier to come up with a fresh adhoc than with a fresh DP problem), but let's not forget about other 95% of population. For a lot of them, even something like manipulating things in a set may be exciting (especially with a great real life statement). So I think when asking for opinions like in Anton's post, it's important to include a great range of people with different skills; similar thing applies to setting contests.
Defining a problem
For the lack of clarity, people use a lot of words to describe the recent trendy problems. Ad-hoc, math, constructive, etc, etc. Let's not pick on these words ("hey, it's not constructive at all!"), because I feel they are used interchangeably for the lack of a clear concept. So what is the current "trend"? I feel there are several things to describe it (only some of them may apply):
- It's very observation oriented (you consider problem on paper or computer to find some patterns, etc). After you notice something, it becomes easy.
- It doesn't require much of well-known algorithms and techniques (including, but not limited to, dp, graphs, data structures, sets/maps, etc), and doesn't fit into these standard categories.
- Often it feels like there is not much benefit from a computer, and implementation is light.
- It could be purely math competition problem, or not too far from it.
- I also notice that a lot of these problems have very artificial statement and setting (like you are given array/permutation and some weird limits/operations/structure, and you need to find something). For me, that indeed doesn't add beauty to the problem, and feels repulsive, but of course it's subjective.
Related to the previous point. A lot of people try to describe what they want, but do it poorly. They say: we want more data structures/dp/graphs/implementation/standard problems/etc etc. I think there is again a lot of ambiguity and a lack of clear concept, so let's not criticize it as "not every contest should have a DP/data structure problem", or "there shouldn't be standard problems" — this is clearly not what people actually want. Let's also not say that "ad hoc problems matter" or constructive problems are cool. That's also of course true, but I think that's not what this debate is about. So what is it about?
I think people generally don't fight against adhoc/constructive problems themselves. They fight against unbalanced distributions in a lot of recent contests, and I agree with them. When there are too many problems with a similar topic, it becomes boring. If the recent trend was "2-3 binary search problems in every contest", then people would fight against binary search too. I think people don't mean "there shouldn't be adhoc problems", or "we want graph problems in every contest", or "DP never appears anymore" — they just say they see a big skew to adhoc problems recently, and it's a valid concern.
So what to do?
I think an important discussion would be what is a good problem distribution in a contest should be. Some points:
- I think it's very possible to give "algorithms/data structure/implementation" problems even as div2 A-D. "Data structure" here can be something as simple as sorting, or using a set, or making elements unique, or a simple parsing. There are a lot of problems that can be set with these.
- Implementation is also important. I, and I think a lot of other people, find implementation interesting too. Figuring how to best implement something that doesn't seem very elegant at first is a great problem as of itself in programming competitions.
- Problems in a contest can be beautiful, but their combination can still be bad. I think Global Round 9 is a great example of this. When first 5-6 problems don't need almost any algorithms and are done as "play with a problem on paper, then code something trivial when done" – it gets boring.
- Let's look at famous well prepared contests, like NEERC ICPC semifinals, IOIs (and other OIs), and Google Code Jam rounds. They often have a great distribution. If there were 50% of adhoc problems there, that would be weird, right?
So what is a great distribution for a contest? I may suggest doing something like this to get a good distribution.
- Let's take a well prepared team contest (like NEERC ICPC semifinal), exclude everything that is team competition related and not suitable for individual contests (really hard data structures, hard geometry, etc), shrink number of problems to 5-6, and take that.
- Or let's take 8-10 random problems from a good online judge (like Timus, or even CF archive itself), again throw away too hard or weird problems, and that should be good.
- And anyway if more than 30% of your problems are on the same wide topic, or feel artificial, or something, you should reconsider it and mix things up.
What are your ideas for a good distribution? And what do you generally think on the debate?









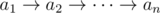 ,
, 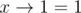 , for all
, for all  or its suffix with at least two arguments.
or its suffix with at least two arguments. there is no solution, for longer inputs any attempt to put parentheses will decrease the number of
there is no solution, for longer inputs any attempt to put parentheses will decrease the number of 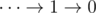 we don't need any parentheses, the value of this expression is always
we don't need any parentheses, the value of this expression is always  (where second missed part consists of ones only). Then
(where second missed part consists of ones only). Then  .
.
