It was a beautiful journey full of internet digging, searching for patterns, learning stuff, fighting with formulas on paper, making crazy observations, coming up with brilliant ideas, implementing crazy optimizations, waiting for the programs to finish, suffering when something was wrong, and so on (and each of the mentioned not once not twice took multiple hours).
It's been a couple of months since I was left with the last unsolved problem and finally I did it! I didn't give up and I obtained the answer alone, without anyone's help, like in the rest of the problems (I was using only internet sources created before the publication of the problem). I'm writing this blog because I am bursting with joy and I wanted to share it with the community. I highly recommend PE as most of the problems were definitely very high quality (and some were a real pain in the ass, but they still teach how to overcome stuff that you're uncomfortable with).
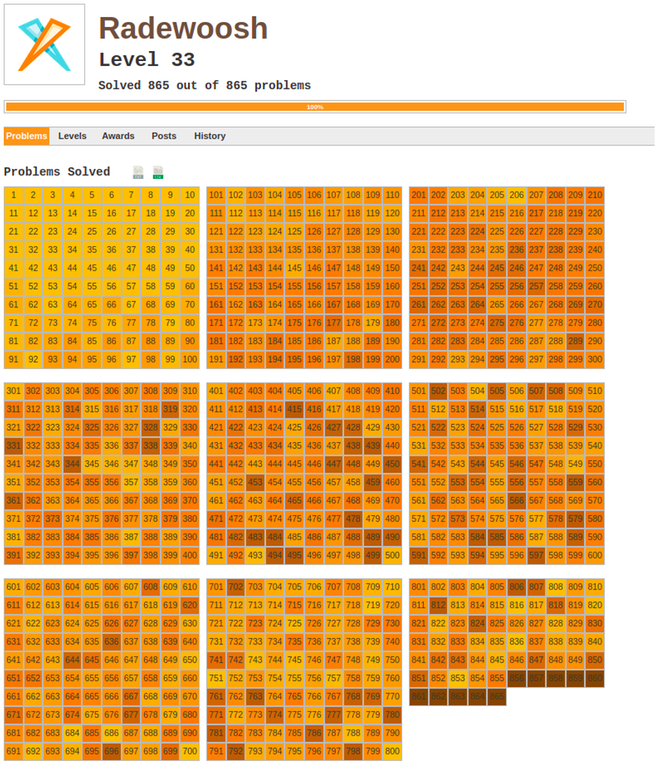
Here's a little souvenir for me:
PS I still have no clue how to do anything useful with continued fractions.