Author: Milesian
Author: liouzhou_101
Author: liouzhou_101
Author: Milesian
Author: Milesian
Author: liouzhou_101
1738G - Anti-Increasing Addicts
Author: antontrygubO_o
Author: liouzhou_101
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Author: Milesian
Author: liouzhou_101
Author: liouzhou_101
Author: Milesian
Author: Milesian
Author: liouzhou_101
1738G - Anti-Increasing Addicts
Author: antontrygubO_o
Author: liouzhou_101
Hello, Codeforces Addicts!
On Sep/30/2022 17:35 (Moscow time) we will host Codeforces Global Round 22. 
Codeforces Global Round 22 is the $$${\textbf{2}} \cdot {\textbf{2}} = 4$$$-th round of a 2022 series of Codeforces Global Rounds. The rounds are open and rated for everybody.
The prizes for this round:
The prizes for the 6-round series in 2022:
Thanks to XTX, which in 2022 supported the global rounds initiative!
The problems were written and prepared by antontrygubO_o, Milesian and me.
We are extremely grateful to the following people who made this round possible:
Round Information:
Kind Tips:
We are looking forward to your participation!
UPD. Editorial
Congratulations to the winners!
And for the winner of each problem:
A. tourist
B. tourist
C. wind_cross
D. tourist
E. tourist
F. 300iq
G. ksun48
H. rainboy
UPD: Solutions are added.
1480A - Yet Another String Game
1479A - Searching Local Minimum
1479B2 - Painting the Array II
Hello, Codeforces!
I'm very glad to invite you to my contest Codeforces Round 700 (Div. 1) and Codeforces Round 700 (Div. 2), which will be held on Feb/07/2021 17:35 (Moscow time). In both divisions, you will be given 6 problems and 2 hours 15 minutes to solve them. One of these problems is interactive, please see the guide of interactive problems if you are not familiar with it.
I would like to thank:
antontrygubO_o for rejecting problems his amazing coordination and discussion.
zjq2863974342 for all his rejected problems becoming the protagonist "Homer" in our problems in honor of his contribution.
lavender730 for all her rejected problems sharing problem ideas and selecting the date of this round.
choutii for discussion and being the first tester of this round (even before the testing phase).
300iq, Retired_cherry, Aditya_Mittal_31, dorijanlendvaj, gamegame, coderz189, Sugar_fan, HIS_GRACE, Invincible06, jiangshibiao, JOHNKRAM, littlefriend, lucifer1004, lyuankai, Milesian, mohammedehab2002, moreD, p_b_p_b and kalki411 for testing and their invaluable feedback.
MikeMirzayanov for the great Codeforces and Polygon!
I have tried my best to write clear problem statements and make strong pretests. I hope you like the problems and enjoy the round.
You can read the story through Codeforces Round #655 (Div. 2), Codeforces Global Round 10 and Codeforces Round #663 (Div. 2).
The anti-traditional score distribution (yes, very early, that's why we call it anti-traditional; I love early score distributions!) is given as follows:
Div. 1: $$$500 - (750 + 750) - 1500 - 2250 - 4000$$$
Div. 2: $$$500 - 1000 - 1500 - (1500 + 1500) - 3000$$$
UPD: Editorial is out.
UPD1: We are sorry for the issue with the problem D2B and for D2C=D1A turning out to be well-known. Constraints for D2B were changed from $$$10^9$$$ to $$$10^6$$$ and all submissions which didn't get AC during the contest were rejudged.
We apologize once again and thank you for your participation.
UPD2 Congratulations to the winners:
Div 1:
1. Petr
2. A.K.E.E.
3. ko_osaga
4. Isonan
5. Benq
Also congratulations to hos.lyric (the only contestant who solved E during contest time!)
Div 2:
1. 5002ryx
2. AlanChen
3. whx1003
4. zkou
5. Ritos__
DFS is commonly used in those problems about trees and graphs. However, an unpopular guy — STACK OVERFLOW — often appears.
The issue about the size of the stack is discussed here. However, only a few languages have been discussed there. For example, in CodeForces platform, the stack size of C/C++ is 256MB, while, that of JAVA is poorly 64MB. MikeMirzayanov said he would change it but it seems he forgot it (or at least the stack overflow issue is not resolved for every language). Fortunately, at least there is a solution for JAVA with threads. Why threads? It seems there is the only way to set stack size at the code (against compile) level in JAVA. Moreover, thanks to CodeForces that threads (in JAVA) have not been banned so far.
The Kotlin Heroes Episode will be held in a few days. While I am using Kotlin, the STACK OVERFLOW issue comes out. It seems there is no blog that talks about this issue at least at this moment. I have struggled for it for days and fortunately resolve it finally. I'd like to share the solution with you, and hope it will help for you.
I first noticed that Kotlin could use JAVA libraries in Petr's code in Kotlin Heroes Episode 1. I combine Kotlin code with the previous solution to stack size for JAVA, and then find that it really works. Since there is still a little difference between Kotlin and JAVA, it is necessary to post the Kotlin code below.
import java.util.*
import java.io.*
fun main()
{
Thread(null, Main(), "whatever", 1 shl 28).start()
}
class Main : Runnable
{
override fun run()
{
// Treat this function as main function and do whatever you want
// Say goodbye to STACK OVERFLOW
}
}
I'd like to note that the constant 1 shl 28 indicates the size of stack being 256MB.
I am not very familiar to Kotlin. If there is a better way to do this, please share with us.
P.S. I feel really guilty that I've made an awful mistake on the checker.
We read the pseudo code carefully. If we ignore "break", tot will be up to 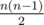 .
.
Consider whether we can make such inequality d ≤ p[j].x - p[i].x is always false. The obvious way is to make all points' x coordinates the same. And we can just choose n distinct numbers to be all points' y coordinate.
Thus the problem is solved.
Consider a number x. If we apply an assignment x = x3, x becomes x3. If we apply such assignment once more, we will get (x3)3 = x32. If we apply such assignment k times, we will get x3k.
Thus, we can get such a sequence a0 = x, a1 = x3, a2 = x32, ..., ak = x3k, ....
Consider a prime p. From Fermat's Little Theorem, we can get xp - 1 = 1(mod p). Further more, we can get xy = xymod(p - 1)(mod p), here a mod b means the remainder of a divided by b.
Fortunately, 348 = 1(mod (95542721 - 1)), thus, x3k = x3kmod48(mod p). In other words, ak = ak + 48, which means the cycle of the sequence is T = 48.
Let's come back to the topic. Each time we run a 1-type query, for every i in the range [l, r], we apply such an assignment ai = ai3. At any moment some i has been applied 48 times such assignments, we can consider this i hasn't been applied any assignments before.
We can use segment tree to solve this problem. Every node of the segment tree maintains some information: the times that we applied assignments in the node's whole range(it's a lazy tag), current sum of the node's corresponding range and the sum of the node's range after we applied assignments k(1 ≤ k < 48) times.
In such a way, we can solve the problem in O(n·T + q·T·logn) time.
If you do not realize how to maintain the segment tree clearly, you can view the code 3782263.
| Name |
|---|


