Do you think you can solve CP problems without reading the problem statements? Let's find out!
On August 28, 2022 (Sunday) 19:30-22:00 GMT+8, I will hold an unofficial fun contest called Statement Not Found. As you can deduce from the title, there will be no problem statements (except title and samples). Your goal is to collect as many points as possible within 2.5 hours :)
Obviously, this round is unrated. It is somewhere between April Fools contest and a legitimate contest.
The contest will be OI-style, meaning there will be no time penalty. You are allowed to use any resources online to help solve the problems. There will be 12 problems.
Scoring Distribution: 200-400-700-700-700-800-800-900-1100-1100-1100-1500 (Total: 10000)
Please read all problems as problem difficulty is very subjective and a 1100-point problem might be easy for you while a 700-point problem might be difficult. The last problem is meant to be a tiebreaker.
You can participate solo or in teams of up to 3 (I would allow more team members but apparently Codeforces doesn't support it). Teams are highly recommended if you intend to solve everything in 2.5 hours. Good luck and have fun!
Twitter Announcement (Japanese)
Below are hints/key insights to all the problems. Of course, please don't open this if you still plan to attempt the problems/virtually participate.
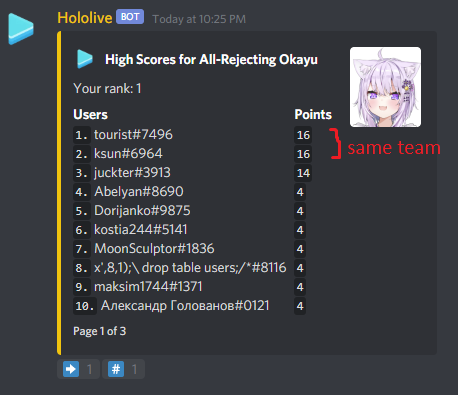
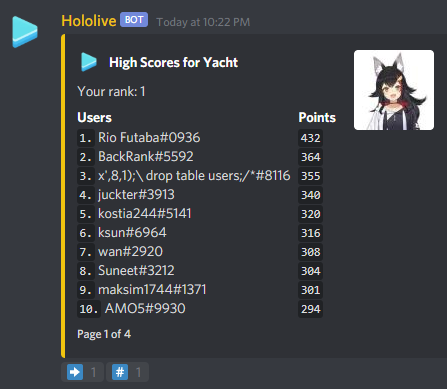
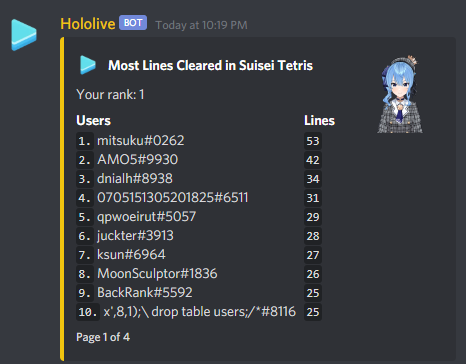
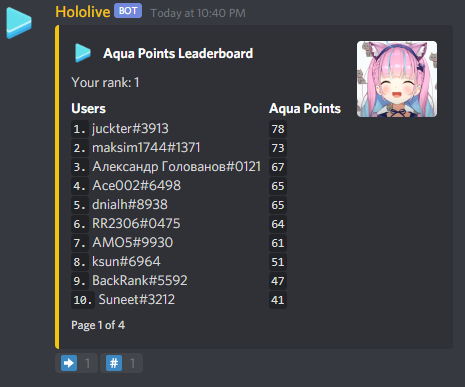
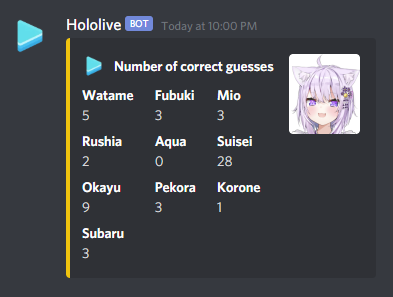
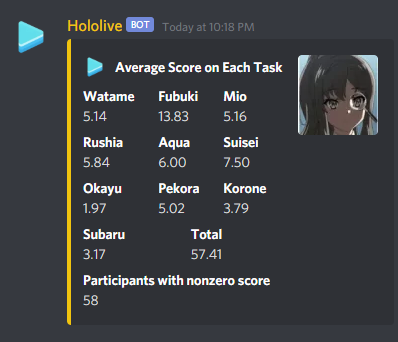
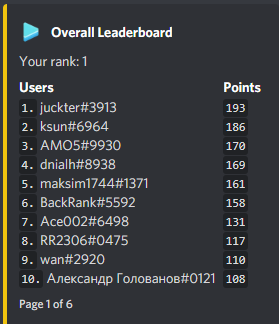
Top Scorers
Golovanov399 6032.144
.I., -is-this-fft- 4625
Gilwall, conqueror_of_tourist, Friday1 4556.109
hitonanode 4400
Bench0310 3900
rainboy 3600
sansen 3456.109
tute7627 3356.109
AndreySergunin 3300










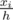 . Since the area of this smaller isosceles triangle is the sum of areas of the first
. Since the area of this smaller isosceles triangle is the sum of areas of the first  of the whole carrot. Thus,
of the whole carrot. Thus,  , which is equivalent to
, which is equivalent to 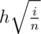 . Thus,
. Thus,  and we can find each
and we can find each 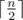 letters and Igor will place
letters and Igor will place 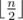 letters. Next, it is clear that Oleg and Igor will both choose their smallest and biggest letters respectively to place in the final string. Thus, we now consider that Oleg places his smallest
letters. Next, it is clear that Oleg and Igor will both choose their smallest and biggest letters respectively to place in the final string. Thus, we now consider that Oleg places his smallest 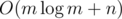 time.
time.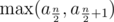 while if
while if 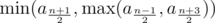 . (If
. (If  time if you use sparse table for range maximum query.
time if you use sparse table for range maximum query.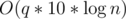 , which is fast enough.
, which is fast enough.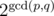 .
.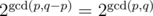 . This proves the claim.
. This proves the claim.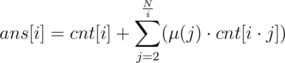 . Thus, this can be computed in
. Thus, this can be computed in 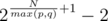 .
.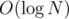 )
)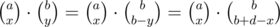 for all
for all 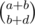 , as the number of ways to choose
, as the number of ways to choose 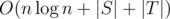 .
.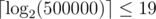 iterations, so the maximum number of operations needed is
iterations, so the maximum number of operations needed is 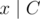 is good, then
is good, then 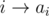 for all
for all 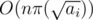 . From now on, we'll focus on a specific prime
. From now on, we'll focus on a specific prime  time.
time.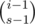 ways to choose the remaining elements of the cycle containing
ways to choose the remaining elements of the cycle containing  for all
for all  time).
time). 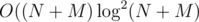 solution, which is relatively simple and demonstrates the idea of slope trick.
solution, which is relatively simple and demonstrates the idea of slope trick. from the initial length of jump. This type of intuition might come in handy to optimize your dp and turn the naive dp into an AC solution.
from the initial length of jump. This type of intuition might come in handy to optimize your dp and turn the naive dp into an AC solution. . (if
. (if 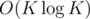 with FFT, but that doesn't really change the complexity since the precomputation already takes
with FFT, but that doesn't really change the complexity since the precomputation already takes 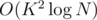 , which fits in the time limit for this subtask.
, which fits in the time limit for this subtask. for all
for all 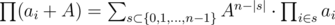 .
.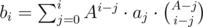 . Indeed, this is just a result of the formula above, where we iterate through all possible subset sizes. Note that the term
. Indeed, this is just a result of the formula above, where we iterate through all possible subset sizes. Note that the term 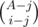 is the number of sets of size
is the number of sets of size 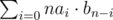 and we can calculate this by multiplying the two polynomials formed by
and we can calculate this by multiplying the two polynomials formed by 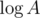 steps. Thus, the total time complexity is
steps. Thus, the total time complexity is  , which can pass.
, which can pass.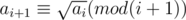 and
and 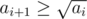 for all
for all 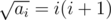 is also a multiple of
is also a multiple of 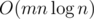 . This is sufficient to pass all tests.
. This is sufficient to pass all tests.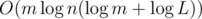 solution.
solution.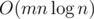 or
or 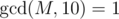 . To find the multiplicative inverse of
. To find the multiplicative inverse of 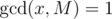 , we have
, we have 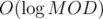 time.
time. 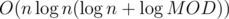 time, where the other
time, where the other 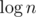 comes from using maps.
comes from using maps.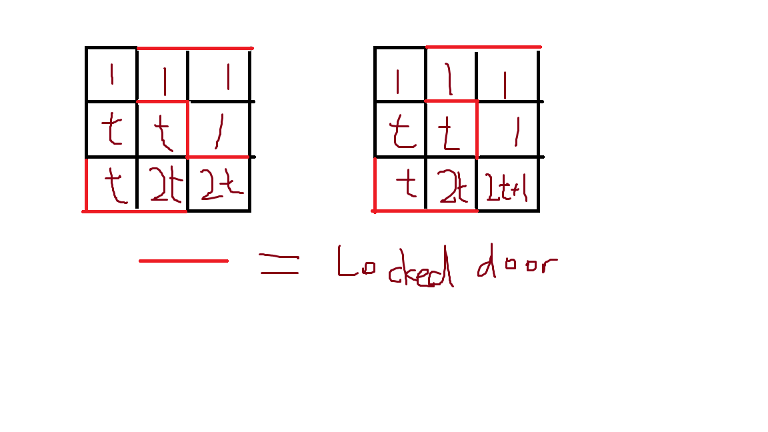
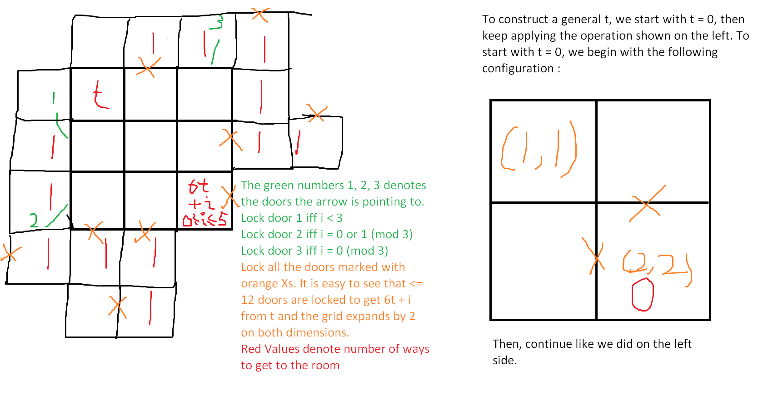
 for all
for all  and is composed of disjoint cycles after
and is composed of disjoint cycles after 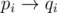 for all
for all  , i.e.
, i.e. 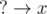 , i.e.
, i.e.  , i.e. both
, i.e. both 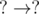 , i.e. both
, i.e. both  , then we increment the total number of cycles by
, then we increment the total number of cycles by  and
and 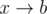 , where
, where 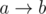 . Clearly, these are the only cases for
. Clearly, these are the only cases for 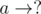 and
and  (where
(where 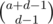 and the number of ways to place the Bs is
and the number of ways to place the Bs is 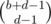 . The number of ways to place the Cs is
. The number of ways to place the Cs is  , since we choose where the Cs should go.
, since we choose where the Cs should go.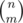 and we can permute them in
and we can permute them in  to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is
to account for the choice of the set of As and Bs used in the A-only and B-only cycles. Thus, the complexity of this method is 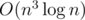 or
or  solutions and enjoy the problems. :)
solutions and enjoy the problems. :) 
