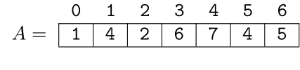
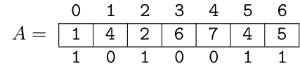
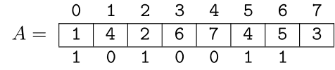
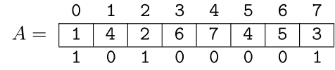
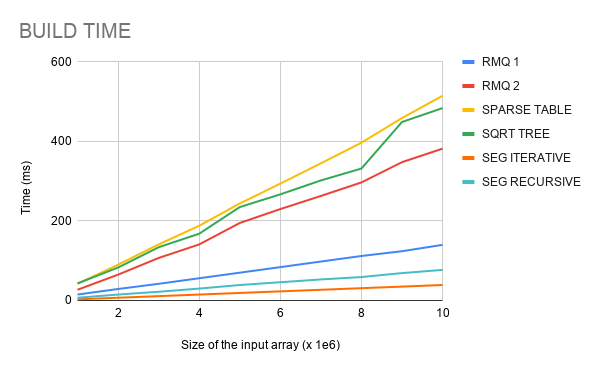
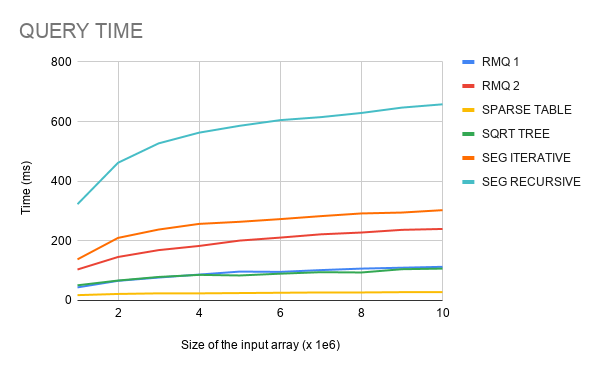
Hello, Codeforces!
I recently had to implement a dynamic convex hull (that supports insertions of points online), and I think the implementation got really small, comparable even to standard static convex hull implementations, and we get logarithmic inclusion query for free. We can:
- Add a point to the convex hull in $$$\mathcal O(\log n)$$$ amortized time, with $$$n$$$ being the current hull size;
- Check if some point belongs to the hull (or border) in $$$\mathcal O(\log n)$$$ time.
Upper Hull
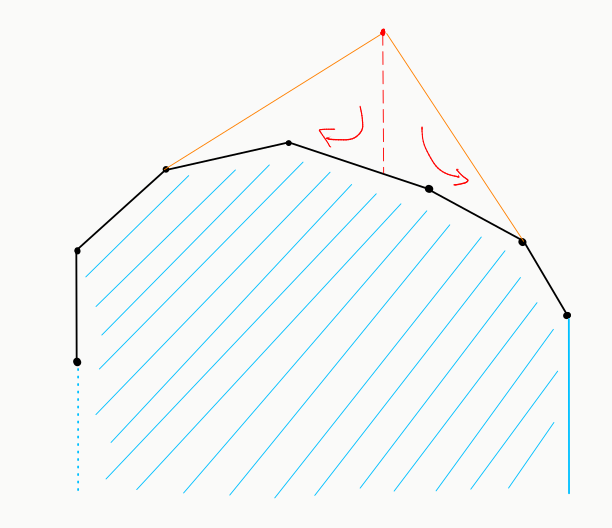
We can maintain the upper hull in a std::set (see below for image, upper hull is in black). We define the region that is under the upper hull as the region in blue, that is, the region that is, well... under. Note, however, that this region is open on the left.
To add a point (red) to the upper hull, we check if it is inside the blue region. If it is, we do nothing. If not, we need to add it, but we might need to remove some points so it continues to be convex. This is done by projecting the red point down (using lower_bound on our set) and iteratively removing points to the right and to the left, while they satisfy the corresponding direction condition.
bool ccw(pt p, pt q, pt r) { // counter-clockwise
return (q-p)^(r-q) > 0;
}
struct upper {
set<pt> se;
set<pt>::iterator it;
int is_under(pt p) { // 1 -> inside ; 2 -> border
it = se.lower_bound(p);
if (it == se.end()) return 0;
if (it == se.begin()) return p == *it ? 2 : 0;
if (ccw(p, *it, *prev(it))) return 1;
return ccw(p, *prev(it), *it) ? 0 : 2;
}
void insert(pt p) {
if (is_under(p)) return;
if (it != se.end()) while (next(it) != se.end() and !ccw(*next(it), *it, p))
it = se.erase(it);
if (it != se.begin()) while (--it != se.begin() and !ccw(p, *it, *prev(it)))
it = se.erase(it);
se.insert(p);
}
};
Convex Hull
Now, to implement the full convex hull, we just need an upper and lower hull. But we do not need to implement the lower hull from scratch: we can just rotate the points $$$\pi$$$ radians and store a second upper hull!
Be careful: if the hull has size 1, the point will be represented in both upper and lower hulls. If the hull has size at least 2, then both the first and last points in the upper hull will also appear in the lower hull (in last and first position, respectively). The size() function below is adjusted for this.
struct dyn_hull { // 1 -> inside ; 2 -> border
upper U, L;
int is_inside(pt p) {
int u = U.is_under(p), l = L.is_under({-p.x, -p.y});
if (!u or !l) return 0;
return max(u, l);
}
void insert(pt p) {
U.insert(p);
L.insert({-p.x, -p.y});
}
int size() {
int ans = U.se.size() + L.se.size();
return ans <= 2 ? ans/2 : ans-2;
}
};
Conclusion
This implementation is considerably small and also not too slow (the constant factor of std::set operations is not small, but if is in function of the hull size, which in some applications can me small). We also get the logarithmic time query to check if some point is inside the hull.
Removing a point from the convex hull is much trickier, and since our runs in amortized logarithmic time, this can not be modified to support removals.









 $$$\hspace{30pt}$$$
$$$\hspace{30pt}$$$