Going to be 100% honest here, I sent problem H to goodbye. I feel really bad to authors of Goodbye 2023 for ruining their round, it seems the round would have been better by just removing H. As much as the community is out here roasting 74TrAkToR, I also had a part to play in this contest. I wish to be as transparent as I can here without saying any classified information (apologies to KAN and 74TrAkToR if anything here shouldn't be disclosed).
To give some context, here is what went down in goodbye round from my perspective:
- 13 days before contest: KAN asks me if I can source a 1E for goodbye. I asked traktor to send me the testing gym so that I could gauge how hard the 1E should be. He told me he will send me after he translates the statements. (UPD: Note that the IMO 1986 problem was already removed before this stage which is why a new 1E was needed, I never saw this IMO problem)
- 11 days before contest: traktor send it to me the testing gym after translating the statements to english
- 10 days before contest: I look at the problems and tell traktor that old G already appeared before (UPD: in APIO 2021, which I participated, so I did not google it)
- 9 days before contest: I confirmed with traktor that he still needed a problem to append to the contest as I thought old G was appended recently. I knew codeton 5 had 2 extra problems that were 1F difficulty so I asked if goodbye could take one of them. I assumed authors already ensured that problem was not googleable cause they only found the problem with $$$O(n^2)$$$ on some chinese OJ. I also implemented A-F and gave comments on them.
- 7 days before contest: H prepared, traktor sent me a buffed version of old G that I couldn't solve
- 6 days before contest: Endagorion tested and comments "H — from a theoretical point of view, this is a super standard exercise From a practical point of view, the only unclear place is what to do when p has a small order modulo 998" . In a discord group chat with Endagorion and authors of H, we resolved the p small order issue
- 4 days before contest: I asked for clarification for buffed version of old G cause it actually seemed impossible, ghosted by traktor
- 2 days before contest: Current G was added to the gym and traktor asked me to try and I misread the statement
- 1 day before contest: I told traktor my current ideas for the misread version of G (I couldn't implement it cause I was overseas)
- day of contest: I realized I misread G a few hours before contest so basically my feedback on G was kind of bullshit

Well, I'm sorry to break the illusion it turns up I was the bad coordinator here. But here are my thoughts on some things organisational wise that all coordinators should do to prevent such things from happening again.
Make a discord server for rounds
Simply, you are just removing the coordinator as the middle man of being the message forwarder. This creates many problems. A trivial one is that if I'm not awake (or just lazy) to forward messages, stuff will be delayed to be sent. But the more serious one is that you won't have transparency between authors and testers. And it may be just a personal feeling, but I feel more compelled as a tester to help out when there is an active server of people rather than just my dms to a coordinator (maybe Endagorion can give his opinion of testing pinely 3 vs testing goodbye).
However, some cons of this is that not all countries allow their citizens to use discord (such as China). If anyone has suggestions for an alternative social media platform, I would be happy to hear it so that I don't have to use wechat.
As an example:
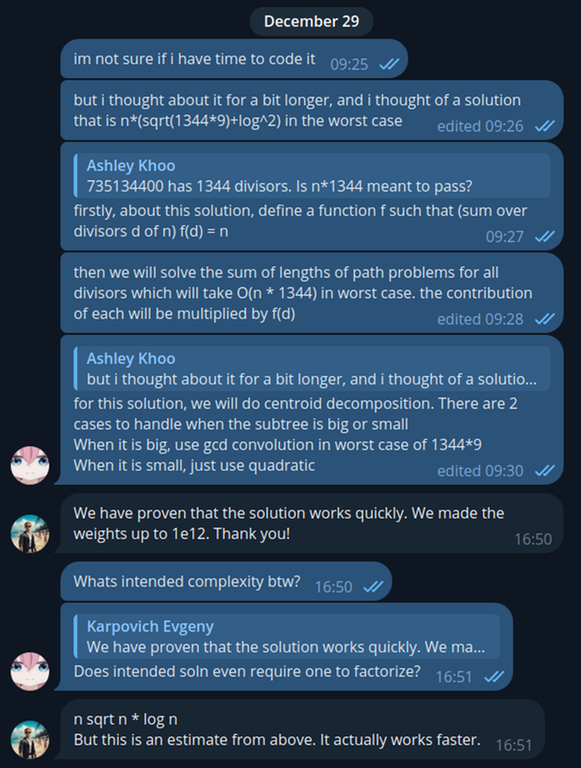
This was my feedback for G, I somehow misread the problem wrongly in 2 places
- I thought the weights are on vertices instead of on the edges
- I thought we wanted to find the sum of values instead of the max value
I'm not sure how this wasn't caught by 74TrAkToR or the authors which I would assume he sent these messages too since defining the function $$$f$$$ is complete bullshit for getting max value. I suppose that if this discussion happened in a testing server with all testers, someone would quickly point out that I'm being stupid and I would actually think of solving the true problem. Funny story, only when I was talking with htetgm about the problems (which is technically breaking the testing rules XD) then I realized that I misread G XDDD.
Ensure that round is ready before even scheduling the contest
I think it becomes apparent that many of the issues of this round was made due to changing many problems in the span of a week before the contest is held. This can be easily negated by testing the round sufficiently early. Personally, I do not schedule contests until I am sure that I do not expect any more changes to the problem set, so in the time period between scheduling and the contest being held, the only thing that authors need to care about is making sure preparation is good, not making even more problems. As such, if you message me or authors about wanting to test the round after the announcement blog is posted, most likely you will be ignored as there is really no point in testing only a few days before the contest. Because realistically we can't make any changes based on your feedback.
As much as I would like to think that I'm a "good" coordinator, stuff like me putting problems that already exists in a contest happens more often than you think. The only reason you (almost) don't see them in contests I coordiante is cause of the testing phase where testers (mostly from China lol) tell me that the problem is already well-known. Of course, this problem being so easily googleable was still a massive oversight and I still take responsibility for this. Yes, I was aware of Endagorion finding H to be standard and I agree with him that it is standard (but I wasn't aware that it was googleable). Under normal circumstances where we had more time, I definitely would have changed it to another problem.
However, it seems that these days there are simply too little div 1 rounds to go around for the number of needed rounds (recently it is pinely 3, goodbye, hello and I predict that there might not be div 1 rounds for a while after these contests...). As such, I had to schedule pinely 3 before I was confident in the problem set and there we had many problem changes in the few weeks to the contest (https://codeforces.com/blog/entry/123449 did not help). But thankfully TheScrasse had a stock of already-prepared problems to switch around and is really efficient at preparing problems (orz).
WE NEED MORE COORDINATORS
The main issue here that there are simply there are too little div 1 coordinators. I would like to appeal to MikeMirzayanov to officially make the process for non-Russian speaking coordinators to be more open. To be completely transparent, I am only a coordinator now because I message MikeMirzayanov that I would like to be a coordinator (of course, I hope people don't start spamming mike now about wanting to be a coordinator). I recall that I had conviction to become a coordinator after testing that div 2 round with barely legible statements and I thought "damn bruh, I can probably do better". Well, for the people who cares about CP and wants to see more great rounds on codeforces, hopefully MikeMirzayanov will make this "application to become a coordinator" more official. Personally, I am not sure how long I am able to keep coordinating at this pace as I am kind of getting burnt up (sorry to all authors who I've ghosted 💀) and being in the military full-time doesn't really help. That being said, even if people are willing to coordinator, how many people have the luxury of having too much time to coordinate? I only have this luxury cause during my highschool days I pretty much didn't care about school and now in military most of my day is spent doing nothing.