Greetings Codeforces Community!
Hope you are doing well, practicing social distancing and are continuing to learn during this time.
The CodeChef April Long Challenge will begin soon! That means 10 days of intense non-stop coding where you can learn while competing in a contest.
The contest will be live from 3rd April till 13th April. So code, learn and don't forget to become a part of this exceptional race to the top of the leaderboard.
The problem statements will be available in English, Hindi, Bengali, Russian, Mandarin, and Vietnamese.
Also if you have some original and engaging problem ideas, and you’re interested in them being used in the CodeChef's contests, you can share them here.
Code against Programmers from all over the globe in this thrilling contest! Accompanying me on the problem setting panel are:
- Setters: Kritagya Agarwal, hackslash_123 (Raj Khandor), dvyn01 (Divyanshu Pandey), BohdanPastuschak (Bohdan Pastuschak), pieguy (David Stolp), 300iq (Ildar Gainullin), Dragonado (Chaithanya Shyam), Ashish Lal
- Tester: fmota (Felipe Mota)
- Editorialist: taran_1407 (Taranpreet Singh)
- Statement Verifier: Xellos (Jakub Safin)
- Admin: Alex_2oo8 (Alexey Zayakin)
- Russian Translator: Mediocrity (Fedor Korobeinikov)
- Vietnamese Translator: Team VNOI
- Bengali Translator: solaimanope (Mohammad Solaiman)
- Hindi Translator: Akash Shrivastava
- Mandarin Translator: Ioser (Hanlin Ren)
Contest Details:
Time: 3rd April 2020 (1500 hrs) to 13th April 2020 (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: https://bit.ly/APRIL20-Codeforces
Registration: You just need to have a CodeChef handle to participate. For all those who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Prizes: Top 20 performers in the Indian category and top 10 performers in the Global category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. First to solve each problem except challenge — 100 laddus. Know more here: https://goodies.codechef.com/
Good Luck! Hope to see you participating! Happy Programming!









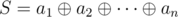 and
and 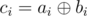 . Suppose that the cards with indices
. Suppose that the cards with indices 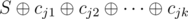 , that is,
, that is, 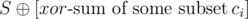 . Hence we want to find the number of subsets
. Hence we want to find the number of subsets  , as applying
, as applying 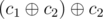 . Thus we can freely replace
. Thus we can freely replace 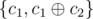 . This means that we can apply the following procedure to simplify the set of
. This means that we can apply the following procedure to simplify the set of 
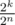 , so the first player wins with probability
, so the first player wins with probability 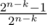 .
.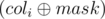 . Suppose that
. Suppose that 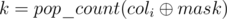 ones. Then we can obtain either
ones. Then we can obtain either 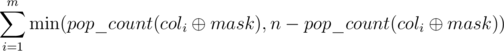 .
.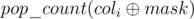 . Let
. Let 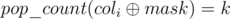 , then for a fixed bitmask
, then for a fixed bitmask 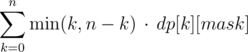 .
.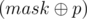 differ in exactly
differ in exactly 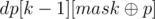 , except we counted in also the number of columns
, except we counted in also the number of columns 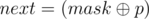 ; by expanding this inclusion-exclusion type argument, we get that the number of masks we are interested in can be expressed as
; by expanding this inclusion-exclusion type argument, we get that the number of masks we are interested in can be expressed as 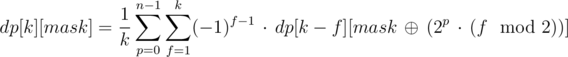
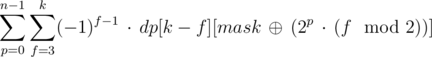
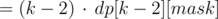
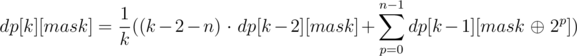

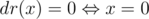 , so, if
, so, if 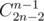 is too big, but we can brute force all possible states. It's not hard to observe that all cells that corresponds to some string
is too big, but we can brute force all possible states. It's not hard to observe that all cells that corresponds to some string 
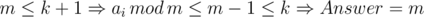
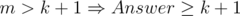 . In this case we will brute force answer from
. In this case we will brute force answer from 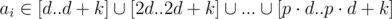 , where
, where 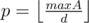 . Since all these intervals
. Since all these intervals 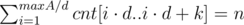 , where
, where 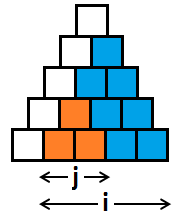
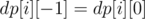 .
.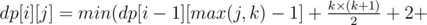
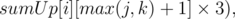
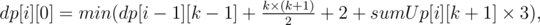
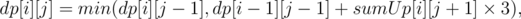 for all
for all 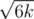 , because for such subpyramid we will pay
, because for such subpyramid we will pay 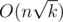 .
.
